Непрерывность функции
Определение 1. Функция f (x)называется непрерывной в точке х0, если предел функции и ее значение в этой точке равны, т.е.: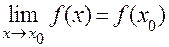 
.
ПРИМЕРЫ:
1. Функция y = x2 будет непрерывной в точке х0 = 2, поскольку выполнено условие определения: предел этой функции и ее значение в этой точке равны между собой и равны 4.
2. Функция y = 1/x не будет непрерывной в точке х0 = 0, поскольку в этой точке не существует предел функции, а также не определена сама функция.
Сформулируем еще одно определение непрерывности функции в точке. Дадим аргументу х0 приращение Δх, тогда функция y = f (x) получит приращение Δy = f (x0 + Δx) – f (x0). Заметим, что в этом случае условия Δх →0 и х →х0 будут равносильны.
Определение 2. Функция y = f (x) называется непрерывной в точке х0 , если она определена в некоторой окрестности этой точки и при приращении аргумента, стремящегося к нулю, приращение функции также стремится к нулю, т.е.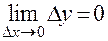 
.
Перечислим основные свойства функций, непрерывных в точке:
| Если функции f (x) и g (x) непрерывны в точке х0, то функции: f (x) ± g (x), f (x)∙g (x) и f (x)/g (x) (при условии g (x) ≠ 0) будут также непрерывными в точке х0. |
| Если функция y = f (x) непрерывна в точке х0 и f (x0) ≠0, то существует некоторая окрестность точки х0, в которой функция f (x) имеет тот же знак, что и f (x0). |
| Если функция z = φ (x) непрерывна в точке х0, а функция y = f (z) непрерывна в точке z0 = φ (x0), то сложная функция y = f [φ (x)] будет непрерывна в точке х0. |
Определение 3. Точка х0 называется точкой разрыва некоторой функции, если в этой точке эта функция не является непрерывной.
Точки разрыва различных функций можно подразделить на точки разрыва двух родов.
Определение 4. Точка х0 называется точкой разрыва первого рода функции f (x), если в этой точке функция имеет конечные, но не равные друг другу, правый и левый пределы.
ПРИМЕР: Для функции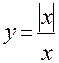 
точка х0 = 0 будет точкой разрыва первого рода, поскольку в этой точке правый и левый пределы этой функции существуют конечны, но не равны друг другу:
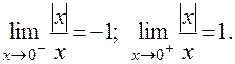
Определение 5. Точка х0 называется точкой разрыва второго рода функции f (x), если в этой точке функция не имеет по крайней мере одного из односторонних пределов, или хотя бы один из них бесконечен.
ПРИМЕР: Для функции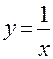 
точка х0 = 0 будет точкой разрыва второго рода, поскольку: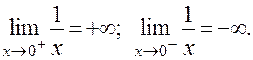 
Функция y = f (x) называется непрерывной на промежутке Х, если она непрерывна в каждой точке этого промежутка.
Можно показать, что все элементарные функции непрерывны в области их определения.
Функция y = f (x), заданная на отрезке [a, b] называется непрерывной на этом отрезке, если она непрерывна в каждой внутренней точке этого отрезка, или в каждой точке интервала (a, b).
Перечислим основные свойства функций, непрерывных на отрезке:
Дата добавления: 2016-04-11; просмотров: 1761;