Классификация функций
Постоянная функция f (x) = С, степенная функция f (x) = xα, показательная функция f (x) = ax, логарифмическая функция f (x) = loga x, тригонометрические функции: sin x, cos x, tg x, ctg x и обратные им функции: arcsin x, arcos x, arctg x, arcctg x называются простейшими элементарными функциями.
Все функции, полученные с помощью конечного числа арифметических действий и (или) конечного числа суперпозиций простейших элементарных функций составляют довольно обширный класс элементарных функций.
Класс элементарных функций, в свою очередь, может быть подразделен на подклассы: рациональных, иррациональных и трансцендентных функций.
Функции вида: Pm (x) = a0 xm + a1 xm-1 + … + am-1 x + am , где m ≥ 0 и целое число, а коэффициенты а с различными индексами – любые действительные числа и а0 ≠ 0, называются целыми рациональными функциямиили многочленамистепени m. При этом, многочлен первой степени (m = 1) называется линейной функцией, а многочлен нулевой степени (m = 0) называется постоянной функцией.
Функции, представляющие собой отношение двух многочленов разных степеней, т.е. функции вида: R (x) = Pm (x)/Qn (x) называются дробно-рациональными функциями.
Совокупность целых рациональных и дробно-рациональных функций образует подкласс рациональных функций.
Функции, полученные с помощью конечного числа суперпозиций и (или) четырех арифметических действий над степенными функциями как с целыми, так и с дробными показателями, и не являющиеся рациональными, называются иррациональными. Например,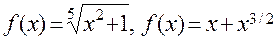 
и т.д. Эти функции образуют подкласс иррациональных функций.
Всякая функция, не являющаяся рациональной или иррациональной, относится к подклассу трансцендентных функций.Например,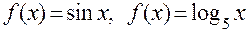 
и т.д.
Примером неэлементарной функции является функция y = ΙxΙ, график которой представлен на рис. 3.
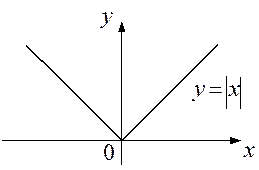
Рис. 3.
Дата добавления: 2016-04-11; просмотров: 1129;