Тест для самопроверки знаний

По Теме 1. Элементы теории множеств

1. Упорядоченное множество, состоящее из двух элементов, принято обозначать следующим образом:

• {x₁, x₂}
• (x₁, x₂)
• [x₁, x₂]

2. Пересечением двух множеств A и B называется множество С, состоящее:

· из всех элементов, принадлежащих хотя бы одному из этих множеств.

· из всех элементов А, не принадлежащих В.

· из всех элементов как множества А, так и В

3. Объединение С двух множеств А и В принято обозначать следующим образом:

· C = A ∩ B

· C = A U B

· C = A \ B

4. Разность D двух множеств А и В принято обозначать следующим образом:

· D = A ∩ B

· D = A / B

· D = A \ B

5. Интервал (-5, + ∞) есть множество:

· неограниченное.

· ограниченное

· замкнутое

6. Отрезок [-3, 2] есть множество:

· неограниченное

· ограниченное

· разомкнутое

7. Точная нижняя грань множества Х есть:

· наибольшее из чисел, ограничивающих множество сверху

· наибольшее из чисел ограничивающих множество снизу

· наименьшее из чисел ограничивающих множество снизу

Тема 2. Числовые последовательности

Основные понятия и примеры

Если каждому натуральному числу 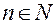по некоторому закону поставлено в соответствие одно действительное число x_n , то множество действительных чисел {x₁, x₂, …, x_n, …} называется числовой последовательностью, или просто последователь­ностью. Числа x₁, x₂, x₃, … называются элементами или членами последовательности, а число x_n – общим элементом (членом) последовательности.

Последовательность считается заданной, если задана формула общего элемента последовательности, как некоторая функция от номера n.

ПРИМЕРЫ:

· арифметическая прогрессия: {2n – 1} = {1, 3, 5, 7, …}.

· геометрическая прогрессия: {2ⁿ} = {2, 4, 8, 16, …}.

· гармоническая последовательность: {1/n} = {1, 1/2, 1/3, 1/4, …}.

Последовательность {x_n} называется возрастающей (убы­ваю­щей), если для каждого 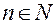справедливо неравенство x_n < x_n+1 (x_n > x_n+1).

Последовательность {x_n} называется неубывающей (невоз­раста­ю­щей), если для каждого 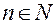справедливо неравенство x_n ≤ x_n+1 (x_n ≤ x_n+1).

Все такие последовательности принято называть монотон­ными.