Основные операции над множествами

Элементы теории множеств

Понятие множества

В математике все понятия делятся на первичные и определяемые через первичные, или уже известные. Первичные понятия не определяются, а, как правило, разъясняются на примерах.

Основным фундаментальным первичным понятием математики является понятие множества. Простейшими примерами множеств можно считать: множество студентов данного института, множество студентов 1 курса, множество всех натуральных чисел и т.д.

Таким образом, множество может содержать конечное или бесконечное количество однородных объектов произвольной природы, называемых элементами или точками.

Математические множества могут состоять из векторов, чисел, функций, матриц и других объектов. Множества обозначаются прописными буквами A, B, C и т.д. Элементы множества обозначаются строчными буквами a, b, c и т.д.

Если x есть элемент множества X, то пишут 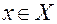(х принадлежит Х). Запись 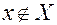означает, что элемент х не принадлежит множеству Х.

Если все элементы множества А являются также элементами множества В, то говорят, что множество А содержится в множестве В. Если 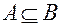, то множество А называется подмножествоммножества В, а если при этом , то множество А называется собственным подмножеством множества В и обозначается: .

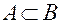Множество, не содержащее ни одного элемента, называется пустым и обозначается знаком Ø. Пустое множество является подмножеством любого множества.

Множество называется конечным, если оно содержит конечное число элементов: А=(а₁,а₂,…,а_n). Множество называется бесконечным,если оно содержит бесконечное число элементов.

Числовые множества задаются на оси действительных чисел, которую принято обозначать R. Наиболее часто используются следующие числовые множества: N – множество натуральных чисел, Z – целых чисел, Q – рациональных чисел, отрезок [a, b], интервал (a, b).

Если каждому элементу одного множества поставлен в соответствие один и только один элемент другого множества, то говорят, что между множествами установлено однозначное соответствие. Если такое соответствие установлено в обе стороны, то оно называется взаимно однозначным соответствием, а такие множества называют эквивалентными.

Счетное множество – это множество, эквивалентное множеству натуральных чисел N. Для того множество А было счетным, необходимо и достаточно, чтобы оно имело вид: 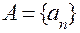, где 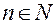. Счетное множество иногда называют упорядоченным, а его элементы записывают в круглых скобках: .

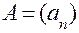Мощностьконечных множеств определяется числом их элементов. Континуумом называется мощность множества действительных чисел.

Основные операции над множествами

Объединениеммножеств А и В называется множество С, состоящее из всех элементов, принадлежащих хотя бы одному из этих множеств: С = А U В, причем: А U Ø = А.

Пересечением множеств А и В называется множество D, состоящее из всех элементов, одновременно принадлежащих каждому из этих множеств: D = A ∩ B.

Разностью множеств А и В называется множество Е, состоящее из всех элементов множества А, не принадлежащих множеству В: E = A \ B.

ПРИМЕР: Для двух множеств А = {1, 3, 6, 8} и B = {2, 4, 6, 8} объединением будет множество C = {1, 2, 3, 4, 6, 8}, пересечением будет множество D = {6, 8}, а разностью – множество E = {1, 3}.