Предел последовательности
Число а называется пределом последовательности {xn}, если для любого числа ε > 0 существует номер N такой, что для всех номеров n > N выполняется неравенство Ι xn – a Ι < ε.
Неравенство Ι xn – a Ι < ε можно переписать в следующем виде: a – ε < xn < a + ε. Геометрически последние неравенства означают, что числа xn принадлежат интервалу (а – ε, а + ε). Поэтому понятие предела имеет следующую геометрическую интерпретацию: число а будет являться пределом последовательности {xn}, если для любого интервала (а – ε, а + ε) существует номер N такой, что для всех номеров, больших этого номера, соответствующие элементы последовательности обязательно будут принадлежать указанному интервалу.
Существование предела последовательности {xn} обозначается следующим образом: 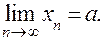
Бесконечно большие последовательности не имеют предела, поэтому принято считать, что они имеют бесконечный предел, и писать: 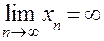 . .
|
Бесконечно малые последовательности имеют
предел, равный нулю, т.е.: 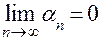 . .
|
Последовательность называется сходящейся, если она имеет предел, и расходящейся, если она предела не имеет, или имеет бесконечный предел.
Последовательность {xn} называется ограниченной, если существует число M > 0 такое, что для всех элементов последовательности выполняется неравенство Ι xn Ι< M.
| Всякая сходящаяся последовательность имеет единственный предел |
| Всякая сходящаяся последовательность ограничена |
| Всякая монотонная и ограниченная последовательность имеет предел |
Для отыскания пределов различных последовательностей существуют полезные правила, справедливые только для сходящихся последовательностей.
Если 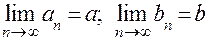 , то:
, то:
1. 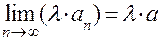 .
.
2. 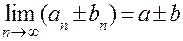 .
.
3. 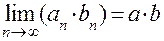 .
.
4. 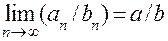 при условии, что все bn ≠ 0 и b ≠ 0.
при условии, что все bn ≠ 0 и b ≠ 0.
Рекомендуемая литература по теме 2:[1 ÷ 2].
ВОПРОСЫ для самопроверки знаний по теме 2:
1. Будет ли монотонной последовательность с одинаковыми членами?
2. Будут ли числа 0 и 1 пределами последовательности {0, 1, 0, 1, …}?
3. Можно ли из ограниченной последовательности {1/n} извлечь (выделить) бесконечно большую последовательность?
4. Пусть число 5 является пределом последовательности. Будет ли конечным число членов этой последовательности, содержащихся в интервале (3,5; 4,5)?
Дата добавления: 2016-04-11; просмотров: 1446;
