Грани числовых множеств

Непустое множество Х называется ограниченным сверху, если существует число С такое, что для любого элемента 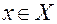выполняется неравенство x ≤ C. При этом число С называется верхней гранью множества Х.

Непустое множество Х называется ограниченным снизу, если существует число с такое, что для любого элемента 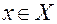выполняется неравенство x ≥ c. При этом число с называется нижней гранью множества Х.

Если множество ограничено и сверху и снизу, оно называется ограниченным. Ограниченное множество обладает верхней и нижней гранями.

Существуют множества, неограниченные снизу (сверху), или с обеих сторон.

ПРИМЕРЫ: Множество [2, 5] – ограниченное, т.к., по крайней мере, числа 2 и 5 являются гранями этого множества. Множество натуральных чисел N ограничено снизу (числом 1 и любым другим числом, меньшим 1) и не ограничено сверху, т.е. – неограниченное. Множество целых чисел Z не имеет граней с обеих сторон и является неограниченным.

Любое ограниченное сверху (снизу) множество имеет бесконечно много верхних (нижних) граней, которые образуют множество чисел, ограничивающих это множество сверху (снизу). Возникает вопрос существования таких граней, которые были бы единственными и характеризовали рассматриваемое множество.

Точной верхней гранью множества Х называется наименьшее из чисел, ограничивающих множество сверху; обозначение sup X.

Точной нижней граньюмножества Х называется наибольшее из чисел, ограничивающих множество снизу; обозначение inf X.

ПРИМЕРЫ: Для множества X = [3, 6] можно записать: sup X = 6 и inf X = 3. Для множества Y = [2, +∞) запишем: inf Y = 2, а точной верхней грани это множество не имеет, т.е. sup Y = +∞.

Свойство точной верхней (нижней) грани:как бы мало ни было число ε > 0, обязательно найдется число 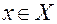такое, что будет справедливо неравенство: x > sup X – ε (x < inf X + ε).

Теорема. Любое непустое ограниченное сверху (снизу) числовое множество имеет свою точную верхнюю (нижнюю) грань.

Рекомендуемая литература по теме 1:[1 ÷ 2].