Тема 3. Функции одной переменной

Понятие функции

Пусть X и Y – некоторые числовые множества. Функцией f называется множество упорядоченных пар чисел (x, y) таких, что: 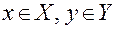и каждое число х в одну и только одну пару этого множества, а каждое число y входит по крайней мере в одну пару этого множества. При этом говорят, что числу х поставлено в соответ­ствие число y и пишут y = f (x). Число y называют значением функции в точке x. Переменную y называют зависимой переменной, а переменную x – независимой переменной (или аргументом); множество Х– областью определения функции, а множество Y – множеством значений функции.

Примерами функций, используемых в экономике, являются: функция спроса, которая выражает зависимость спроса на некоторый товар от его цены; функция предложения – выражает зависимость предложения некоторого товара от его цены; производственная функция – выражает зависимость объема выпускаемой продукции от объема перерабатываемого ресурса и т.д.

Задать функцию f (x) означает указать, каким образом для каждого значения аргумента х находить соответствующее ему значение функции y = f (x). Функции можно задавать:

· аналитически, т.е. с помощью формул;

· с помощью таблиц;

· графически.

ПРИМЕРЫ:

1. Зависимость между величиной дохода х и величиной спроса y на товары первой необходимости задается функцией Торнквиста, аналитическое задание которой имеет вид:

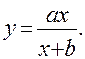
2. Налоговая ставка для конкретно выбранных доходов может быть задана таблицей:

3. Функция Торнквиста, приведенная в примере 1, может быть задана графически – рис. 1.

Рис. 1.

Над функциями, если они имеют общую область определения, можно производить различные арифметические операции: умножать функции на число или друг на друга; делить друг на друга; складывать, вычитать и т.д.

Если на некотором множестве Х определена функция z = φ (x) с множеством значений Z, а на множестве Z определена функция y = f (z), то функцию y = f [φ (x)] принято называть сложной функцией от х, или суперпозицией (наложением) функций φ (х) и f (z), а переменную z – промежуточной переменной сложной функции.

ПРИМЕР:Функция y = sin (x²) является сложной, поскольку она представ­ляет собой суперпозицию двух функций y = f (z) = sin z и z = φ (x) = x².

Пусть Х и Y – некоторые числовые множества и пусть задана функция f, т.е. множество пар чисел (x, y) в смысле данного выше определения функции. Если в каждой паре этого множества числа х и y поменять местами, то получится множество пар чисел (y, x), которое называется обратной функцией φ к функции f, т.е. x = φ (y).

ПРИМЕР: Для функции y = x² при условии х ≥ 0 функция будет обратной функцией.

Если обратная функция однозначна, то множество значений Y функции f служит областью определения обратной функции φ, а область определения Х функции f – областью значений функции φ.

Функция y = f (x) и обратная ей функция x = φ (y) имеют один и тот же график в декартовой системе координат. Если для данного значения х₁ ищется (по графику) соответствующее ему значение y₁, то используемый график – график функции y = f (x). Если же для данного значения y₂ ищется соответствующее ему значение х₂, то та же линия является графиком функции x = φ (y) (рис. 2):

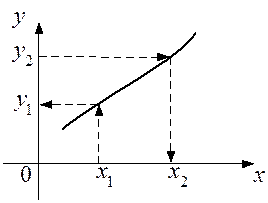
Рис. 2.