Предел функции в точке и в бесконечности
Пусть функция y = f (x) определена на некотором множестве Х, а некоторое число х0 принадлежит этому множеству, или не принадлежит ему.
Определение 1. Число А называется пределом функции f (x) в точке х0 (или при х→х0), если для любой сходящейся к х0 последовательности значений аргумента {xn}, отличных от х0, соответствующая последовательность значений функции {f(xn)} сходится к числу А. При этом записывают: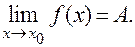 
ПРИМЕР: Предел функции y = x2 в точке х0 = 2 равен 4, или: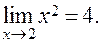 
Определение 2.Число А называется правым (левым) пределом функции f (x) в точке х0, если для любой сходящейся к х0 последовательности значений аргумента, элементы xn которой больше (меньше) числа х0, соответствующая последовательность значений функции сходится к числу А.
Приняты следующие обозначения таких пределов: правый предел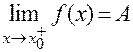 
; левый предел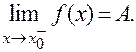 
ПРИМЕР: Для функции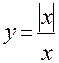 
определенной для всех х ≠ 0 на основании определения модуля имеем: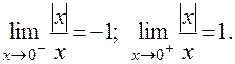 
| Функция имеет в точке предел тогда и только тогда, когда в этой точке существуют как правый, так и левый пределы и они равны между собой. В этом случае предел функции в точке равен односторонним пределам в этой же точке. |
ПРИМЕР:Функция, рассмотренная в предыдущем примере, в точке х0 = 0 предела не имеет, поскольку существующие правый и левый пределы этой функции в этой точке не равны между собой.
Можно определить предел функции в точке и другим способом на языке (ε, δ).
Определение 3.Число А называется пределом функции f (x) в точке х0, если для любого числа ε > 0 существует число δ > 0 (зависящее от ε) такое, что для всех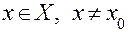 
и удовлетворяющих неравенству 
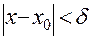, выполняется неравенство 
.
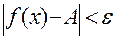Геометрический смысл этого определения состоит в том, что если число А является пределом функции f (x) в точке х0, то для всех значений аргумента х, содержащихся в δ – окрестности точки х0 , соответствующие значения функции попадут в ε – окрестность числа А (рис. 4):
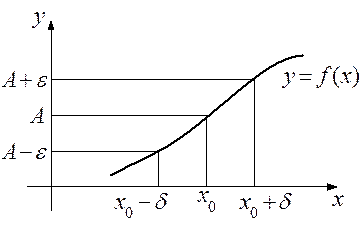
Рис.4.
Определение 4. Предел функции y = f (x) в точке х0 равен +∞ (−∞), если для любой последовательности {xn} значений аргумента, сходящейся к х0, соответствующая последовательность значений функции {f (xn)} является бесконечно большой, т.е. имеет своим пределом + ∞ (− ∞).
Аналогично определяются правый и левый бесконечные пределы функции в точке.
ПРИМЕРЫ:Для функции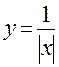 
имеем: 
. Для функции 
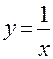можно записать: 
.
Определение 5. Число А называется пределом функции f (x) при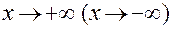 
, если для любой бесконечно большой последовательности значений аргумента, элементы которой положительны (отрицательны), соответствующая последовательность значений функции сходится к числу А.
ПРИМЕР:Для функции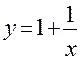 
в соответствии с определением можно записать 
.
Для пределов функций выполняются следующие важные для практического применения свойства:
| Пусть функции f (x) и g (x) имеют в точке х0 пределы, равные В и С, и а – любое число. Тогда функции f (x) ± g (x), f (x)∙g (x), a∙f (x) и f (x)/g (x) (при С ≠ 0) имеют в точке х0 пределы, соответственно равные: В ± С, В∙С, аВ и В/С. |
| Пусть функции f (x), g (x) и h (x) определены в некоторой окрестности точки х0 и для всех х из этой окрестности выполняются неравенства f (x) ≤ g (x) ≤ h (x). Тогда, если функции f (x) и h (x) имеют в точке х0 предел равный А, то и предел функции g (x) в этой точке будет равен А. |
Существуют два стандартных предела, которые традиционно называются замечательными.
Первый замечательный предел: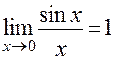 
.
ПРИМЕРприменения:
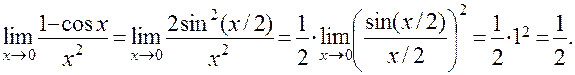
Второй замечательный предел: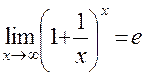 
.
ПРИМЕРприменения: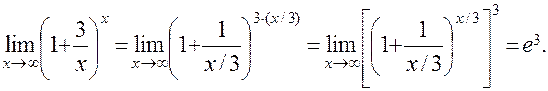 
Дата добавления: 2016-04-11; просмотров: 12225;