Первая теорема Больцано-Коши
Если функция f (x) непрерывна на отрезке [a, b] и на концах отрезка имеет значения разных знаков, то существует точка 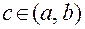 , в которой f (c) = 0. , в которой f (c) = 0.
|
Вторая теорема Больцано-Коши
Если функция f (x) непрерывна на отрезке [a, b],
причем f (a) = A и f(b) = B и С – любое число,
заключенное между А и В, то существует точка
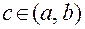 , в которой f (c) = C. , в которой f (c) = C.
|
Первая теорема Вейерштрасса
| Если функция определена и непрерывна на отрезке [a, b], то она ограничена на этом отрезке. |
Вторая теорема Вейерштрасса
| Если функция непрерывна на отрезке [a, b], то она достигает на этом отрезке наименьшего значения m и наибольшего значения М. |
Рекомендуемая литература по теме 3:[1 ÷ 3].
ВОПРОСЫ для самопроверки знаний по теме 3
1. Пусть левый предел функции 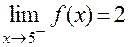 . Может ли при этом быть справедливой запись:
. Может ли при этом быть справедливой запись: 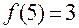 ?
?
2. Пусть предел функции 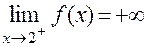 . Может ли при этом быть справедливой запись:
. Может ли при этом быть справедливой запись: 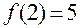 ?
?
3. Существует ли предел 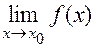 , если существуют пределы:
, если существуют пределы: 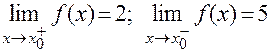 ? Как в этом случае называется точка х0?
? Как в этом случае называется точка х0?
4. Пусть функция 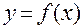 непрерывна на отрезке [1, 3]. Может ли быть
непрерывна на отрезке [1, 3]. Может ли быть 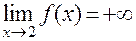 ?
?
Тема 4. Дифференциальное исчисление
Дата добавления: 2016-04-11; просмотров: 1302;
