Определение и смысл производной

Пусть функция y = f (x) определена в некоторой окрестности точки х, тогда приращению Δх аргумента х будет соответствовать приращение функции Δy = f (x +Δx) – f (x). Однако более важным для исследования свойств функции является не абсолютное приращение функции Δy, а относительное приращение Δy / Δx, которое характе­ри­зует направление и среднюю скорость изменения функции в пределах рассматриваемой окрестности точки х.

Определение. Производной функции y = f (x) называется предел относительного приращения функции Δy / Δx при стремлении приращения аргумента Δх к нулю, т.е.:

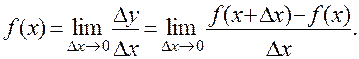
Таким образом, производная функции, вычисленная в данной точке, характеризует мгновенную скорость и направление изменения функции в небольшой окрестности этой точки. В этом и состоит основной смысл производной применительно к исследованию свойств функции.

Геометрический смысл производной состоит в том, что производная функции y = f (x) численно равна угловому коэффициенту касательной к графику функции y = f(x) в точке M (x, f (x)) (рис. 5), т.е.

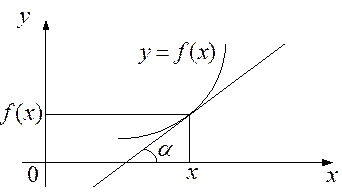
Рис. 5.

Экономический смысл производной (точнее, один из эконо­мических смыслов) заключается в том, что производная производственной функции по времени есть мгновенное значение производительности труда в момент времени t₀.

Пусть функция μ (t) определяет объем продукции, произве­денной за время t, т.е. является производственной функцией. Тогда относительное приращение этой функции Δμ / Δt будет характе­ри­зо­вать среднюю производительность труда за время Δt, а производная этой функции – мгновенное значение производительности труда в момент времени t: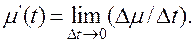

В экономических моделях наряду с отношением приращений функции Δy / Δx рассматривается отношение относительных приращений .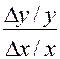

Определение. Эластичностью функции y = f (x) в точке х называется предел отношения относительного приращения функции Δy / y к относительному приращению аргумента Δх / х при стремлении к нулю приращения аргумента Δх, т.е.:

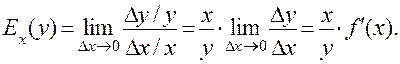
Таким образом, эластичность функции показывает (приближенно) на сколько процентов изменится значение функции при изменении аргумента на 1 процент.

Дифференцируемойв точке называется функция, которая имеет производную в этой точке.

Дифференцируемой на промежутке называется функция, которая имеет производную в каждой точке этого промежутка.

Дифференцированием функции называется операция отыскания производной этой функции.