База знаний и данных

Однозначного определения понятия "знания" не существует. Поэтому будем придерживаться подхода, при котором новое по­нятие раскрывается через набор его специфических характеристик. Прежде чем раскрыть эти характеристики, введем некоторые предвари­тельные понятия.

Переменная- это объект с априорно неизвестным значением. Часто отождествляют все три понятия:

<переменная> = <о6ъект> = <неизвестное значение>.

Переменная может быть связанной и несвязанной (свободной). В последнем случае переменной не приписано какое-либо конкретное значение. Естественно рассматривать само значение как другой объект оп­ределенного типа. С этой точки зрения связанная переменная представляет пару <V₁, V₂> с исходным объектом V₁, представляющим имя переменной, и производным объектом V₂, представляющим значение пе­ременной. При этом, как правило, не имеет значения конкретный вид объекта V₂. Так, пара <Х, "Петр"> интерпретируется как переменная X, связанная со значением символьной константы "Петр".

Некоторые трудности возникают, когда V₂ представляет так называемое автоопределение (рекурсивное определение), например

<Х, Х² - Х +1 >,

или, в более обычной форме X = Х² - X + 1. Если последнее интерпретируется как уравнение, то можно вывес­ти, что X = 1.

Если последнее требуется интерпретировать как подстановку (для Х), то следовало писать

< Х, ²X² - Х +1²> или <X, Y² - Y + 1>.

В последнем случае необходимо обеспечить допустимость использования замены. Например, недопустима замена X = Y в формулеln(X - Y) = ln(X + Y), что приводит к ln 0 = ln 2Y.

Константа,очевидно, может быть представлена как пара <С, С>,где Ссуть конкретный объект. Обозначение <V, V>со связанной пе­ременной V суть также пример константы. Характеристиками знаний являются следующие.

1. Внутренняя интерпретируемость знанийотождествляется нами с наличием некоторой функции (способа) связывания переменных с теми или иными значениями или иначе, - способом порождения пар <V_i, V_j>. Такая функция или способ называется также интерпрети­рующей функцией (или просто интерпретацией).

Поскольку данные - это пары вида <С, С>,где С- константа, то, очевидно, для них не требуется интерпретирующая функция (т.к. дан­ные представляют сами себя).

2. Вторая характерная черта знаний - рекурсивная структурирован­ность и связность.Рекурсивная структурированность определяется через понятие концепта. Концепт есть семантическое целое понятий. Понятие Р₁ и Р₂ образуют семантическое целое, если имеет место какое-то из перечисленных условий:

(А) Р₁ и Р₂ связаны друг с другом как отношение и один из его аргументов;

(В) Р₁ и Р₂ связаны друг с другом как действие и его носитель или субъект;

(С) Р₁ и Р₂ связаны друг с другом как функция и ее аргумент (объект и его свойство).

По индукции следует, что множество P = {P₁, P₂, ..., P_n} понятий образует семантическое целое, если каждый Р_i в Р образует семанти­ческое целое как минимум с одним из Р_j, где P_j Î P/{P_i}.

Концепт С есть упорядоченное множество С_i , где С_i - семантичес­кое целое, содержащееся в семантическом целом, представляющем С.

Рассмотрим концепт С: "Студент Петр сдает экзамен по химии". Здесь можно выделить следующие семантические целые:

С₁ = <Студент Петр> (объект Петр; свойство -студент)

С₂ = <Петр сдает экзамен> (объект Петр; действие - сдает экзамен)

С₃ = <Экзамен по химии> (объект экзамен; свойство - по химии)

Таким образом, исходный концепт С образован простым объе­динением

C = C₁ È C₂ È C₃.

Отметим, что результат не зависит от порядка слагаемых, т.е.

C = C₁ È C₂ È C₃ = C₂ È C₁ È C₃ = C₃ È C₂ È C₁ и т.д.

Рекурсивность операции объединения È показывается элементарно через тождество

Æ È X = X

{a} È X = {a, X} (1.2)

{a, Y} È X = {a} È {X È Y}

3. Семантическое пространство с метрикой.Это свойство знаний связано с возможностью их измерения в системе оценок (метрики) [истинно, ложь]. В системе с нечеткой логикой используется бесконечное множество оценок истинности знания. Например, заключение ЭС вида "завтра ожидается дождь с вероятностью 0,8" не является ни строго истинным, ни строго ложным, т.е. характеризуется определенной степенью правдоподобия.

4. Активность знаний.Это свойство знаний "адаптироваться" под изменяющиеся факты (т.е. способность к обучению и самокоррекции).

5. Функциональная целостность.Под функциональной целостностью знаний понимается их непротиворечивость, независимость исходных посылок и разрешимость. Поскольку понятия непротиворечивости и разрешимости являются фундаментальными понятиями логики, то их рассмотрение вынесено в самостоятельные подразделы. 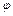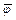Ограничимся здесь указанием на то, что непротиворечивость знаний означает невозможность появления в базе знаний двух взаимоисключающих фактов и (типа "пациент жив" и "пациент мертв"). Хотя прин­ципиально возможно рассуждение на основе противоречивых посылок, т.к. в настоящее время не существует развитой теории для этого случая. Поэтому мы придерживаемся требований классической логики.

Требование разрешимости заключается в том, что любое истинное знание, формализуемое в базе знаний системы, может быть выведено в ней с помощью машины вывода. Требование разрешимости, к сожале­нию, не всегда выполнимо. В частности, как показал А. Черч, неразре­шима в общем случае логика предикатов, о которой пойдет речь немно­го ниже.

6. Независимостьозначает невозможность вывода единого знания из другого формальным способом.

7. Ситуативность.Наличие ситуативных связей определяет совмести­мость тех или иных знаний, хранимых в памяти. В качестве таких связей могут выступать отношения времени, места, действия, причины и пр. Для нас важны модели представления знаний в ЭВМ. При этом основными требованиями к представлению знаний являются однородность представления, простота понимания, непротиворечи­вость и полнота. В существующей практике получили наибольшее распространение следующие модели знаний:

- логическая;

- модель, основанная на использовании правил (продукционная модель);

- фреймы;

- семантические сети.

Понятие модели

В математике моделью (или реляционной системой) называется не­которое множество М с заданным на нем набором отношений {r₁, r₂, ..., r_n}.Как известно,отношение математически пред­ставляется в следующей форме: имя_отношения (список_аргументов).

Когда идет речь о модели знаний, то отнюдь необязательно, чтобы множество М было однородно (состояло только из объектов одной при­роды). Например, отношение "быть владельцем (х, у)" устанавливает, что х есть владелец у, а экземпляр такого отношения

быть_владельцем (Иван, книга)

имеет дело с объектами разной природы. Важно подчеркнуть, что в об­щем случае отношение предполагает некоторую процедуру (называе­мую разрешающей процедурой), которая устанавливает истинность или ложность отношения. Такая процедура может задаваться алгоритмом, правилами, таблицами и иными способами. При этом, всегда стоит вопрос об эффективности (и даже существовании) разрешающей процедуры.

Логические модели

Поскольку логика является основой рассуждений, то ее роль в ме­ханизмах вывода является центральной. В самом общем виде логическая модель знаний - это конечное или бесконечное множество отношений логики предикатов первого порядка, называемых просто логическими формулами формул (конечное или бесконечное) логики предикатов первого порядка ( или просто логических формул). Каждая формула ло­гической модели может иметь лишь два значения - истина или ложь.

Для записи формул используется язык, содержащий алфавит и множество правил, согласно которым образуются (правильно построен­ные) формулы.

Язык логики предикатов задается следующим образом. Алфавит содержит следующие классы символов:

a) переменные, обозначаемые через x, y, z, v, u, ...,

b) константы, обозначаемые посредством a, b, c, d, ...,

c) функциональные символы, представляемые как f, g, h, ...,

d) символы отношений p, q, r, s, ...,

e) символы пропозициональных констант: TRUE (истина) и FALSE (ложь)

f) логические операторы (связки): - (отрицание, НЕ), Ú (дизъюн­кция, ИЛИ), & (конъюнкция, И), ® ( импликация, ЕСЛИ ...ТО), « ( эквиваленция, ЕСЛИ И ТОЛЬКО ЕСЛИ)

g) кванторы: $ (существование), " (всеобщности)

h) круглые скобки (,) и запятую ",".

Для конъюнкции используется также символ Ù, а для эквиваленции « или º.

Каждый символ функции и отношения характеризуется числом аргументов данной функции (отношения) называемым местностью (арностью). Например, функция sin(х) является одноместной, f(x², x, c)- трехместной и т.п.

Далее определим класс термов:

a) переменная есть терм;

b) константа есть терм;

c) если f есть n - местная функция и t₁, ..., t_n - термы, f(t₁, ..., t_n) суть также терм.

Логическая формула задается следующей схемой:

a) если p - n - местное отношение и t₁, ..., t_n - термы, то p(t₁, ..., t_n) есть формула (называемая атомарной)

b) пропозициональные константы TRUE и FALSE суть формулы

c) если F и G формулы, то формулами также являются ( 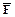), (FÚ G), (F & С), (F®С), (F«С)

d) если F - формула и х - переменная, то ($ х F )и ("х Р ) - также формулы.

Для упрощения записи логических формул часто отбрасывают скобки, используя отношение порядка (старшинства) между логи­ческими операторами и кванторами. Так, будем считать, что -, $, " связывают сильнее, чем &, который в свою очередь связывает сильнее оператора Ú, а последний связывает сильнее, чем операторы ®, «.

Поэтому формулу

("y ("x ((p(x) & ( 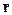(y)))® ( (x)Ú (AÚB))))) (1.3)

можно представить в виде

"y ("x (p(x) & ( 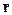(y))® (x)Ú AÚB) (1.4)

Рассмотрим, как представляются знания о предметной области на основе логических формул. Предложение: " Для всех х, если х студент, то сдает экзамены х " может быть представлено как

"x (P(x) ® Q(x)),

где Р- эквивалентно Студент;

Q - эквивалентно Сдает-экзамены.

Следовательно, в эквивалентной нотации, можно записать: "x (Студент (x) ® Сдает-экзамены (x)).

Предложение: "Только артисты восхищаются артистами" получа­ет представление в виде:

" x" y (B(y, x) & A(x)® A(y)),

где А(х) - "x есть артист", В(у, х) - "у восхищается х".

Утверждение ассоциативности арифметической операции сложения имеет следующее формальное представление:

" x" y" z ((x +y) + z = x + (y + z))

Отметим, что последнее выражение с точки зрения правил построения формул логики предикатов следовало записать в виде:

" x" y" z E ((fadd(fadd(x, y), z) fadd(x, fadd(y, z)))),

где Е - предикат равенства ( = );

fadd - двухместная функция сложения;

fadd (t₁, t₂) - терм, представляющий сумму термов t₁ и t_2.

Как видим, последнее представление значительно менее наглядное.

Отличительными чертами логических моделей являются единствен­ность теоретического обоснования и возможность реализации системы формально точных определений и выводов. Основными задачами, решаемыми на логических моделях, являют­ся следующие:

- установить или опровергнуть выводимость некоторой формулы (в общем случае эта задача алгоритмически неразрешима);

- доказательство полноты/неполноты некоторой формально логи­ческой системы, представленной множеством логических формул;

- установление выполнимости системы логических формул (нахож­дение интерпретирующей функции) или отыскание контрпри­мера, опровергающего их;

- определение следствий из заданной системы формул;

- доказательство эквивалентности двух формально-логических систем;

- поиск решения задачи на основе доказательства теоремы существования решения и др.