Понятие формальной системы
Прежде чем мы сформулируем понятие машины вывода, нам необходимо дать определение формальной (аксиоматической) системы и правил вывода. Под формальной системой понимается четверка:
М = <Т, Р, А, П>, (1.10)
где Т - множество базовых элементов;
Р - множество правил построения правильных (сложных) объектов из базовых элементов;
А - множество изначально заданных объектов формальной системы (множество аксиом );
П - множество правил построения новых объектов из других правильных объектов системы.
Для того, чтобы выяснить смысл этих формализмов, рассмотрим введенную ранее логическую модель как пример аксиоматической системы.
В качестве множества базовых элементов Т здесь используются элементы языка логики предикатов: переменные, константы, функциональные и предикатные символы и вспомогательные знаки.
В качестве множества правил Р построения правильных (сложных) объектов логики предикатов выступают правила построения формул логики предикатов.
Например, следующая формула является правильно построенной
(" x( $ y($ z( P(x, y) ® 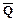 (z))))),
(z))))),
в то время как объект ниже
(x® P(x, y))Ú($ z ( 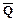 (z)))
(z)))
не является правильно построенной формулой.
Множество аксиом - это множество формул, истинность которых постулируется без доказательства.
Постулаты логики предикатов имеют вид схем аксиом. Схема аксиомы - это математическое выражение, которое дает конкретную аксиому каждый раз при подстановке вместо какой-то буквы одной и той же формулы.
Схемы аксиом логики предикатов таковы:
1. A ® (B ® A)
2. (A ® B) ® ((A ® (B ® C)) ® (A ® C))
3. A ® (B ® A & B)
4.
a) A & B ® A
b) A & B ® B
5.
a) A ® AÚ B
b) B ® AÚ B
6. (A ® C) ® ((B ® C) ® (AÚB ® C))
7. (A ® B) ® ((A ® 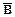 ) ®
) ® 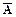 A)
A)
8. 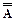 ® A
® A
9. " x A(x) ® A(t)
10. A(t) ® xA(x)
Постулаты арифметики:
1. A(o) & x (A(x) ® A(x’)) ® A(x) (аксиома индукции)
2. a¢ = b¢ ® a = b
3. a = b ® (a = c ® b = c)
4. A + 0 = a
5. a° 0 = 0
6. 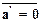
7. a = b ® a¢ = b¢
8. а + b = (а + b)¢
9. a b¢ = a b + a
Здесь A, B, C - формулы; х - переменная; t - терм; a, b, c - целые числа; операция (’) (штрих) соответствует добавлению к числу единицы: а’ = а + 1.
Рассмотрим, например, схему аксиом (7). Заменим формулу А ® В на 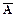 Ú В и подставим (7)
Ú В и подставим (7)
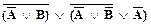
Далее по правилам де Моргана: 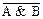 =
= 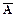 Ú
Ú  получаем:
получаем:
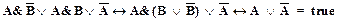
Нетрудно видеть, что схема аксиом (7) является тождественно истинной, если истинна формула A  .
.
Мы, однако, не в состоянии доказать последнюю формулу, т.е. считаем ее истинной по определению.
Воспользуемся примером, иллюстрирующим это положение.
Рассмотрим высказывание "последовательность 0123456789 встречается в разложении числа p". Обозначим это высказывание через А. Тогда обратное высказывание 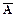 означает, что "последовательность 0123456789 не встречается в разложении числа p". Для того, чтобы доказать формулу А (или
означает, что "последовательность 0123456789 не встречается в разложении числа p". Для того, чтобы доказать формулу А (или 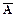 ) в принципе нужно строить бесконечное представление для числа. Поскольку ни один шаг такого "доказательства", если он не приводит к отысканию требуемой последовательности, не является законченным, мы не вправе считать, что доказана формула А (
) в принципе нужно строить бесконечное представление для числа. Поскольку ни один шаг такого "доказательства", если он не приводит к отысканию требуемой последовательности, не является законченным, мы не вправе считать, что доказана формула А ( 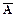 ). Итак, мы в принципе не в состоянии укачать финитное (конечное) доказательство ни для формулы А, ни для формулы
). Итак, мы в принципе не в состоянии укачать финитное (конечное) доказательство ни для формулы А, ни для формулы 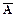 .
.
Будем записывать десятичное разложение числа p, а под ним десятичную дробь r = 0,333.... При записи каждой очередной цифры в разложении p добавляем "3" в r. Если окажется, что высказывание А истинно, то стираем записанное представление для r и полагаем
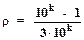
где k - число троек, полученных в представлении к данному моменту.
Допустим, что справедлива формула В 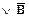 , где В - это высказывание "число рационально", и
, где В - это высказывание "число рационально", и 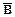 - обратное высказывание, т.е. число не рационально.
- обратное высказывание, т.е. число не рационально.
Спросим себя, рационально ли r или нет? Если r не рационально (верно 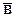 ), то должно быть верно
), то должно быть верно 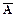 (иначе, если бы была получена последовательность 0123456789), то
(иначе, если бы была получена последовательность 0123456789), то
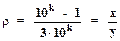
где х, у - целые, т.е. было бы рационально. Однако, если справедливо 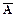 , то r = 1/3 = 0.333... (бесконечная последовательность). Здесь r рационально, что противоречит предположению о его нерациональности. Итак, r не может быть не рациональным. Но значит r рационально. Для этого однако, нужно иметь доказательство А или
, то r = 1/3 = 0.333... (бесконечная последовательность). Здесь r рационально, что противоречит предположению о его нерациональности. Итак, r не может быть не рациональным. Но значит r рационально. Для этого однако, нужно иметь доказательство А или 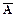 , чего у нас нет.
, чего у нас нет.
Действительно, если r рационально либо мы построили бесконечную последовательность 0,333... (что невозможно), либо доказали формулу А.
Приведенный пример характеризует так называемое интуиционистское направление в математике. Так интуиционисты отрицают правило tertium non datyr (третьего не дано). Ими также подвергается критике само понятие отрицания: ложность любой формулы j трактуется ими так, что допущение j ведет к противоречию.
Еще один философский пример того же рода демонстрирует так называемый парадокс лжеца: "если некто говорит, что он лжет, то говорит ли он на самом деле правду или лжет?"
Обозначим высказывание "Я лгу " через А. Если А истинно, то "некто в действительности лжет", т.е. должно быть 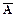 и наоборот. А это означает, что формула A
и наоборот. А это означает, что формула A  ни истинна, ни ложна (противоречива).
ни истинна, ни ложна (противоречива).
Вернемся, однако, к истине (1.10). Нам осталось определить правила вывода П. Каждое правило вывода имеет структуру вида:
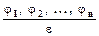 (1.13)
(1.13)
означающую, что если выведены формулы j1, j2, ..., jn, называемые посылками, то выводима также формула e называемая заключением.
Под выводимостью формулы e из формул j1, j2, ..., jn, понимается такое отношение между этими формулами, что всякий раз, когда истинна каждая из формул j1, j2, ..., jn, истинна также формула e.
По определению, аксиома a имеет структуру
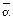 , (1.14)
, (1.14)
т.е. невыводима из других формул (множество посылок пусто).
Отметим следующие основные свойства для отношения выводимости.
1. Рефлективность:
 (1.15)
(1.15)
2. Транзитивность:
 (1.16)
(1.16)
(если j выводима из e и из j выводима g, то из e выводима формула g).
3. Монотонность:
 (1.17)
(1.17)
(если из e выводима формула j, то присоединение к e формулы g не отменяет выводимость j). Отметим, что свойство монотонности в общем случае не имеет места в некоторых неклассических логиках, рассматриваемых в главе 3.
4. Теорема дедукции:
Если из e и g выводима формула j, то из e выводима формула g ® j (® - импликация).
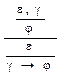 (1.18)
(1.18)
Верна также обратная теорема:
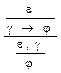 (1.19)
(1.19)
Теорема дедукции имеет весьма важное значение в логике. Действительно, чтобы доказать выводимость
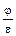 (1.20)
(1.20)
заменим формулу e эквивалентной формулой e Ú , где - символ пустой формулы (лжи). Используя эквивалентную замену e Ú « 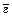 ® , получим
® , получим
|
|
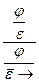 «
« 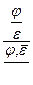 . (1.21)
. (1.21)
|
|
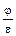 следует показать, что
следует показать, что 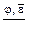 , т.е., что из j и
, т.е., что из j и 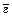 следует противоречие - .
следует противоречие - .
В качестве основных правил вывода в логике предикатов используются правила modus ponens и generalization.
Правило modus ponens:
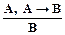 (1.22)
(1.22)
утверждает, что если истинны формулы А и А ® В, то истинна формула B.
Правило generalization:
 . (1.23)
. (1.23)
Справедлива и обратное
 (1.24)
(1.24)
при условии, что С не содержит переменной. х. Это последнее правило существенно важно при реализации наиболее широко применяемого резолютивного вывода, с содержанием которого мы познакомимся позднее.
В частности, если С пустая формула, то имеет место
 (1.25)
(1.25)
Пример правила generalization:

Отметим, что правила вывода в логике предикатов не исчерпывают множества всех известных правил вывода. Однако, правила вывода имеют иное семантическое содержание. Об этом следующий параграф.
Дата добавления: 2016-03-05; просмотров: 1155;
