Модели знаний на основе продукций
В модели знаний на основе продукций знания представлены совокупностью правил в формате "ЕСЛИ - ТО". Рассмотрим, например, правила порождения родительного падежа слов, задаваемые таблицей 1.1.
Для того, чтобы получить родительный падеж слова "Знахарь" отыскиваем первую подходящую строку, начиная с верхней, в левом колонке табл.1.1. Строка будет подходящей, если указываемое в ней окончание совпадает с окончанием слова (в данном случае выбирается строка 5). Нетрудно, однако видеть, что строка 6 также подходит для нашей цели, хотя выдаваемый ею результат (правая колонка табл. 1.1.) не верен. Прежде чем мы рассмотрим более подробно это свойство системы продукций, выясним их природу. Рассматривая структуру продукции, нетрудно видеть, что ее условная часть ("ЕСЛИ...") определяет ситуацию, в которой продукция применима. В примере со словом " знахарь" ситуация определяется его окончанием, т.е. либо окончанием "арь", либо ''-ь".
Таблица 1.1.
| № п/п | Слово или его окончание в именительном падеже | Слово или его окончание в родительном падеже |
| 1. | кино | -кино |
| 2. | -ча | -чи |
| 3. | -ка | -ки |
| 4. | -а | -ы |
| 5. | -арь | -аря |
| 6. | -ь | -и |
| 7. | -ие | -ия |
| 8. | -мя | -мени |
| 9. | -я | -и |
Если ситуация удовлетворяет продукции, то в результате ее применения может быть получен новый объект (состояние) согласно части " ТО ... " в структуре продукции. Так, применение продукции с номером 5 в табл.1.1. к слову "знахарь" порождает слово "знахаря", а применение продукции номер 6 дает слово "знахари". Таким образом, одним из основных вопросов в реализации продукционных систем является стратегия выбора альтернативных правил. В общем случае эта проблема нетривиальна. Условная часть продукции может иметь различные формы, такие например, как в следующих примерах:
² ЕСЛИ (идет - дождь) ²;
² ЕСЛИ (a > b2 - b) ²;
² ЕСЛИ (P C Q) ².
В структуре продукции дополнительно могут указываться метка и строка, содержащая объяснение применения продукции. Метка может быть простым идентификатором (или номером) или некоторым пояснительным текстом, например, "определение окраски инфекции по Граму" Строка-объяснение показывает, почему используется продукция. Следующий пример демонстрирует полную продукцию:
МЕТКА: R26 Использование зонтика
УСЛОВИЕ: ЕСЛИ (идет дождь)
ДЕЙСТВИЕ: ТО (возьмите зонтик)
ОБЪЯСНЕНИЕ: (зонтик предохраняет от дождя)
Как правило, задача, формулируемая для продукционной системы, имеет одну из следующих структур
<S0, Sf - ?> (1.5)
<S0 - ?, Sf> (1.6)
<S0, Sf, A - ?> (1.7)
<S0, Sf - ?, A - ?> (1.8)
где: S0 - начальная ситуация, Sf - конечная (желаемая, требуемая ситуация), А - алгоритм (последовательность выполняемых продукций), переводящий систему из состояния S0 в состояние Sf
Задача (1.5) связана с определением ситуации (состояния) Sf, удовлетворяющей некоторому критерию, которая может быть получена из заданной начальной ситуации.
Задача (1.6) является обратной по отношению к предыдущей.
Задача (1.7) заключается в отыскании алгоритма преобразования начальной ситуации в конечную.
Задача (1 .8) представляет обобщение задач (1 .5) и (1 .7).
Продукции удачно моделируют человеческий способ рассуждений при решении проблем. Поэтому продукции широко используются во многих действующих ЭС. Система MYCIN, фрагмент которой приведен во введении, а также ее более поздняя редакция EMYCIN являются примерами продукционных систем.
Продукционные системы впервые изобретены Постом в 1941г. Продукция в системе Поста имеет следующую схему
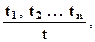 (1.9)
(1.9)
где t1, t2, ..., tn называются посылками, а t заключением продукции.
Применение схемы (1.9) основывается на подстановке цепочек знаков вместо всех переменных, причем вместо вхождений одной и той же переменной подставляется одна и та же цепочка.
В качестве других классических продукционных систем отметим нормальные алгоритмы Маркова и машину Тьюринга.
Развитием модели на основе правил является модель "доски объявлений". Эта модель реализована в системе распознавания разговорной речи HEARSAY - 2. Основной принцип организации модели доски объявлений заключается в разбиении продукций по уровням иерархии. При этом заключения продукций на нижних уровнях используются как входные условия для продукций более высокого уровня. На нижнем уровне модели доски объявлений представлены факты, на верхнем - результирующее заключение.
Иерархическое разбиение множества продукций позволяет более эффективно организовать их выполнение, существенно сократив затраты на перебор множества продукций при проверке условий их срабатывания, что определяет дополнительный интерес к продукционным системам.
В рамках этой модели продукция определяется четверкой:
P = < L, C, N, A >,
где L – метка;
С – условие применимости;
N– ядро продукции, описываемое формулой (1.9);
А – постдействие.
Дата добавления: 2016-03-05; просмотров: 948;
