Примеры стратегии вывода
Рассмотрим формализм нормальных алгоритмов Маркова, в котором правила вывода реализуются на основе операторов подстановки.
Пусть а и b - произвольные слова. Будем говорить, что слово а входит в слово b, если существуют такие слова с и d, что b = cad.
Основным правилом вывода является подстановка. Оператор подстановки а ® b используется для замены левого вхождения слова а на слово b. Для того, чтобы применить оператор а ® b к слову e, необходимо, чтобы е содержало а. В последнем случае будем говорить, что выполнены условия применимости оператора а ® b. Из множества операторов, для которых выполнены условия применимости, всегда выбирается один оператор (например, первый по порядку). Отметим, что вывод считается детерминированным, если всякий раз условия применимости выполняются не более чем для одного правила вывода. Алгоритм завершает работу, если либо нет выполнимых операторов, либо выполняется специальный оператор конца (стоп-оператор).
Пример.
(1) a ® bc
(2)c ® ebcc
(3)c ® d
(4)d ® e
(5)b ® e
(6) есс ® d.
e - символ пробела.
Рассмотрим, как преобразуется в этой системе слово cad:
 cad ® ebccad ® eccad ® dad ® ad ® bcd ® cd ® ebccd ® eccd ® dd ® d ® e
cad ® ebccad ® eccad ® dad ® ad ® bcd ® cd ® ebccd ® eccd ® dd ® d ® e
Здесь внизу под стрелкой указан номер оператора.
В системах нормальных алгоритмов Маркова выводимость трактуется в конструктивном смысле - как получение из исходного слова (образца) других слов. Это - так называемый вывод по образцу (нашедший применение, например, в системах, использующих фреймы и семантические сети). Каноническая продукционная система Поста также является системой вывода по образцу.
Пусть x1, x2, ..., xn - попарно различные переменные, которые имеют области определения D1, D2, ..., Dm соответственно. Если переменная х связана некоторым значением 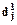 из Dj, , то будем вместо х, писать
из Dj, , то будем вместо х, писать 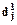 .
.
Образец t это конструкция
t 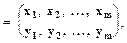
где каждому xi, сопоставлен терм уi , являющийся либо самой переменной хi, (если она не связана), либо 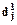 , если xi =
, если xi = 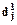 .
.
Например,
t1 = 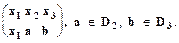
Пусть даны два образца t1 и t2. Будем говорить, что из t1 и t2 выводится образец t3, и писать это: 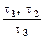 , если выполнены следующие условия:
, если выполнены следующие условия:
1) t1 и t2 содержат общие переменные
2) пусть xi - одна (любая) из общих переменных, тогда xi и в t1, и в t2 либо связана одним и тем же значением, либо как минимум одна из них не связана вовсе.
3) t3 образуется путем включения (без дублирования) всех переменных из t1 и t2. При этом если общая переменная xi связана, скажем в t1, значением хi = а, а в t2 свободна ( не связана), то в t3 xi будет иметь значение а. В этом случае говорят, что переменные в t3 наследуют значения соответствующих переменных в t1, t2.
Пример вывода по образцам t1, t2 образца t3.
t1 = 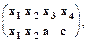
t2 = 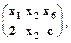
из t1, t2 выводим образец t3
t3 = 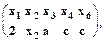
Другой важной стратегией, используемой в машинах вывода, является Байесовская стратегия вывода, которая используется в системах, где детерминированность выводов является скорее исключением, чем правилом.
Байесовская стратегия вывода оперирует вероятностными знаниями. Ее основная идея заключается в оценке апостериорной вероятности гипотезы при наличии фактов, подтверждающих или опровергающих гипотезу. Пусть
Р(Н) = - априорная вероятность гипотезы Н при отсутствии каких- либо свидетельств;
Р(Н:Е) = - апостериорная вероятность гипотезы Н при наличии свидетельства Е.
Согласно теоремы Байеса:
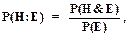 (1.26)
(1.26)
и 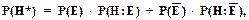
где Р(Н*)оценивает новую вероятность гипотезы Н с учетом свидетельства Е.
Введем отношение правдоподобия ОП(Н:Е),
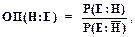 (1.27)
(1.27)
а также формулу для вычисления шансов O(H),
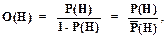 (1.28)
(1.28)
Из (1.28) нетрудно обратным преобразованием получить
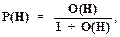 (1.29)
(1.29)
Теперь формула Байеса (1.8) на языке шансов принимает следующий вид:
O(H*) = O(H) OП(H:E),(1.30)
где O(Н*) - новая оценка шансов для гипотезы Н с учетом свидетельства Е.
Формула (1.30) при наличии многих свидетельств E1, E2, ..., En принимает вид:
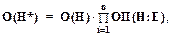 (1.31)
(1.31)
Таким образом, на основании формул (1.30) и (1.31) имеется возможность просто пересчитывать апостериорные вероятности гипотез на основании получаемых свидетельств. Теорема Байеса является основой механизма вывода в экспертных системах PROSRECTOR и HULK.
Рассмотрим пример использования стратегии Байеса. Пусть требуется провести дифференциальную диагностику между заболеваниями D1, D2, ..., Dn. Для простоты, пусть имеется три заболевания и четыре признака, по которым должен быть составлен диагноз.
Заболевания:
D1 - тетрадаФалло, D2 - дефект межпредсердечной перегородки, D3 - незараценный артериальный проток.
Признаки:
S1 - цианоз, S2 - усиление легочного рисунка, S3 - акцент II тона во втором межреберье слева, S4 - правограмма (ЭКГ).
Допустим, известны следующие условные и безусловные вероятности (табл. 1.2), полученные на основе накопленной статистики о больных данными заболеваниями.
Таблица 1.2
| Dj | P(Dj) | P(S1/Dj) | P(S2/Dj) | P(S3/Dj) | P(S4/Dj) |
| D1 | 0,35 | 0,9 | 0,05 | 0,6 | |
| D2 | 0,15 | 0,15 | 0,8 | 0,8 | 0,8 |
| D3 | 0,50 | 0,10 | 0,95 | 0,90 | 0,10 |
Пусть у пациента налицо все четыре признака: S1, S2, S3, S4. Каков диагноз заболевания? На основе теоремы Байеса можно оценить апостериорные вероятности заболеваний в предположении, что признаки S1, S2, S3, S4 независимые. Найдем 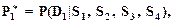
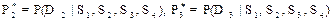
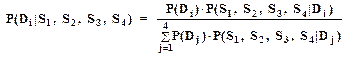 (1.32)
(1.32)
Из условия независимости признаков имеем:
P(S1, S2, S3, S4|Di) = P(S1|Di) × P(S2|Di) × P(S3|Di) × P(S4|Di) (1.32)
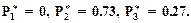
Дата добавления: 2016-03-05; просмотров: 1075;
