Проблема непротиворечивости формализованной базы знаний

При добавлении информации от экспертов в базу знаний, необхо­димо обеспечить непротиворечивость базы знаний. Непротиворечивость означает, что в базе знаний не выводимы никакие два факта (формулы) вида а и 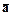(из которых один отрицает другой). Проблема непротиво­речивости не является тотальной, т.е. вполне допустимы противо­речивые системы, однако, нужно иметь в виду следующее.

Во-первых, практически многие хорошо разработанные теории вы­вода работают с непротиворечивыми системами формул. Действитель­но, если система противоречива, то в ней выводимо все что угодно! Это обстоятельство практически лишает смысла само понятие вывода в противоречивой системе. В такой системе, следовательно, вывод заменяется иными механизмами (например, механизмами классификации - распознавания и принятия решений).

Во-вторых, сам характер задачи, стоящей перед СИИ, не допускает противоречивого толкования знаний (например, заключения 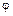: "паци­ента нужно немедленно прооперировать" и 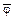: "пациента не нужно не­медленно оперировать" таковы, что неясность в смысле их выбора мо­жет стоить жизни человеку. (Такова, к примеру, фабула романа А. Хейли "Окончательный диагноз").

В формальных логических системах первого порядка противоре­чивость эквивалентна выводимости в системе пустой формулы (интер­претируемой как ложь).

Неизбыточность. Требование незбыточности означает, что в базе знаний хранятся лишь независимые друг от друга знания. Формула 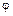зависима от формул x₁, x₂, ..., x_k, если 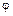выводима из x₁, x₂, ..., x_k в силу правил вывода. Неизбыточность знаний не является императивным требованием. Фактически, избыточность имеет сильный положительный момент, который заключается в следующем.

Пусть СИИ в результате доказательства цели построила цепочку

П_i1, П_i2, П_i3, ..., П_{i n-1}

C₀ ® C₁ ® C₂ ® ... ® C_n,

где С_k - k-ый контекст вывода (k-ое состояние трассы вывода); П_ij - правило вывода (продукция), применяемое к контексту С_j-1.

Это позволяет ввести в базу знаний новую продукцию

,

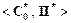где является выводом по образцу из С₀ и С_i1 (C_i1 - условная часть продукции П_i1 ),

П* = <П_i1, П_i2, ..., П_{i n-1}> - представляет последовательную цепоч­ку операционных частей продукций П_i1, П_i2, ..., П_{i n-1}.

Добавление продукции 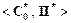в базу знаний при следующем ре­шении задачи < 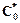, C_n - ?> избавит от необходимости строить план ре­шения задачи снова, т.е. приводит к увеличению быстродействия СИИ. Рассмотрим, как определяется зависимость формул в логике высказывании, являющейся той частью логики предикатов, которая позволяет формализовать фактуальные знания (т.е. знания, представленные сово­купностью фактов). Итак, пусть требуется установить выводимость пропозициональной формулы G, представленной в виде

G = g₁ Ú g₂ Ú g₃ Ú ... Ú g_m, (1.41)

где g_i - формулы (гипотезы), взятые с отрицанием или без него, из формулы F произвольного вида, т.е. доказать справедливость:

F ® g₁ Ú g₂ Ú g₃ Ú ... Ú g_m, (1.42)

Суть предлагаемого метода заключается в последовательном ум­ножении обеих частей (1.42) на 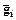, 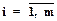. Например, в порядке возрас­тания индекса i, пока не будет получена одна из следующих ситуаций:

(a1) F* ® ð

(a2) F* ® F* (ð®ðили F* ® 1)

(a3) ð® F*,

где ð - символ пустой формулы, ð = х & 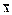; F - непустая формула формальной системы.

Тогда справедливы следующие заключения:

Ситуация (а1) означает невыводимость G из F (G не находится в отношении логического следствия из F);

Ситуация (а2 и а3) означает, что G логически следует из F, 1 = х Ú .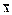

Таким образом, для доказательства произвольной формулыF ® G, ее необходимо привести к виду (1.42) и выполнить описанную процедуру, доказательство которой здесь опускается.

Пример. Пусть даны формулы

f₁ = a ® b&c& ,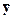

f₂ = b ® 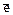&f,

f₃ = c Ú 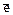® x Ú y.

Покажем, что имеет место

a&f₁&f₂&f₃ ® x.

Умножим обе части нах:

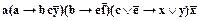®ð.

Заменим (p ® q) на :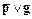

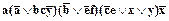®ð.

Откуда, раскрывая скобки, имеем

ð ®ð,

что устанавливает доказываемое соотношение.

С другой стороны, отношение

a&f₁&f₂&f₃ ® y

невыводимо, поскольку имеет место:

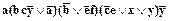®ð.

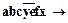Илиð.

Итак, проблема избыточности решается с помощью механизма вы­вода.

Обучение системы

Как уже отмечалось, более менее развитая техника обучения имеет­ся для задач распознавания и классификации. Задача классификации заключается в отнесении предъявленного образца к некоторому классу. В качестве классифицирующей функции может, например, использоваться функция

g(x) = w₁x₁ + w₂x₂ + ... + w_dx_d + w_d+1, (1.43)

Данная функция называется также линейной дискриминаторной функцией. Для того, чтобы использовать линейную дискриминаторную функцию, исходное множество cобъектов разбивается на классы c₁, c₂, ..., c_N, причем каждый объект из cпринадлежит только одному классу c_i.

Для каждого класса некоторым (определенным) образом подби­раются весовые коэффициенты W = <w₁, w₂, ..., w_d+1>. Считается, что предъявленный объект относится к тому классу, для которого значение дискриминаторной функции достигает максимального значения. Рассмотрим, из каких соображений определяются весовые коэффициенты w_i. Прежде всего, для каждого класса выбирается представитель Р_i этого класса.

Расстояние между произвольной точкой X d-мерного пространства и представителем Р_i, вычисляется как

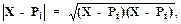(1.44)

где(Х - Р_i )(Х - Р_i) = Х·Х - 2Х · Р_i + Р_i · P_i. (1.45)

Естественно полагать, что точка X принадлежит тому классу, рас­стояние между представителем которого Р_i иX минимально. Поскольку член X×X в (1.45) для всех классов один и тот же, то минимум (-2ХР_i + Р_i Р_i) эквивалентен максимуму(2ХР_i - Р_iР_i). В связи с этим в качестве g_i(Х) используется функция

g_i(X) = 2X×P_i - P_i×P_i. (1.46)

Из (1.46) имеем, что 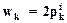где 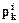- i-ая компонента вектораР_i и w_d+1 = P_i×P_i.

Теперь выясним, в чем заключается процесс обучения. Если заранее не известен представитель каждого класса, то нужно определить подхо­дящим образом весовые коэффициенты w_i, в дискриминантной функции (1.43). Определение весовых коэффициентов осуществляется с помощью обучающей выборки, относительно которой известна результирующая классификация. В качестве обучающей выборки для СИИ может высту­пать накопленный опыт решения задач классификации. Рассмотрим ал­горитм непараметрического обучения, как он описан. В качестве начальных весов выбираются произвольные векторы, изменение кото­рых производится только в случае неправильной классификации объек­тов. Допустим, при классификации объекта Y он неверно относится к классу ), вместо отнесения его к классу 1. Тогда весовые векторы, используемые как в 1-ой, так и в 1-ой дискриминантных функциях, изменяются следующим образом:

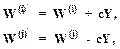(1.47)

где 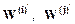- новые весовые выходы; с - коэффициент коррекции.

Таким образом, исправление состоит в увеличении дискриминантной функции W⁽ⁱ⁾ и уменьшении дискриминантной функции W⁽ⁱ⁾. Также доказывается, что приведенный обобщенный алгоритм обучения находит разделяющие весовые наборы за конечное число исправлений.

Отметим в заключении этого параграфа, что обучение может быть связано также с выдвижением гипотез и методами индуктивных рас­суждений. Соответствующие формализмы были предложены в начале века Д.С.Миллем.