Извлечение знаний от многих экспертов
Извлечение знаний от экспертов ставит следующие проблемы:
(1) в какой форме осуществляется диалог с экспертами?
(2) как обрабатывать информацию, представленную экспертами?
Первая проблема состоит в том, что СИИ "не имеет представлений" о том, что она призвана решать. Иначе говоря, она либо ведет один и тот же сценарий диалога, либо вообще является пассивной стороной, представляя эксперту набор директив редактора базы знаний. Однако, даже и в этом последнем случае встает проблема, чтобы введенная экспертом информация:
(а1) была непротиворечивой;
(а2) не нарушала целостность существующей базы знаний;
(а3) не была "пустой" или избыточной.
Таким образом, обеспечение требований (а1 - а3) является важнейшей функцией модуля извлечения знаний и обучения.
Рассмотрим, как осуществляется обработка экспертной информации на примере системы диагностирования. Предположим, эксперты оценивают некоторый диагноз (гипотезу), указывая оценки правдоподобности (коэффициенты уверенности - КУ) этой гипотезы. Таким образом, каждый эксперт формирует пару (Н, КУi),где Н- некоторая гипотеза. Если обозначить через a1, a2, ..., an - степени компетентности экспертов (веса), то результирующее значение КУ* для гипотезы Н полагаем равным:
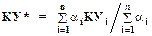 (1.36)
(1.36)
При отсутствии информации о компетентности экспертов можно положить ai = 1 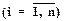 .
.
Для оценки статистической значимости найденного значения КУ* находят дисперсию
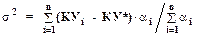 (1.37)
(1.37)
и далее, задавшись вероятностью ошибки Рош, определяют вероятность (1 - Рош), с которой случайная величина попадает в интервал
[КУ* - D; КУ* + D], (1.38)
где 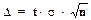 и t- коэффициент Стьюдента, устанавливаемый из таблиц по значению Рош и n.
и t- коэффициент Стьюдента, устанавливаемый из таблиц по значению Рош и n.
Другой важной задачей при экспертизе является ранжирование продукций с учетом их важности. Очевидно, что от того, насколько точно ранжированы правила, определяется эффективность стратегии вывода.
В результате процедуры ранжирования строится следующая таблица (табл. 1.4)
Таблица 1.4.
| Эксперты | Продукция | |||
| m | ||||
| r11 | r12 | r1m | ||
| r21 | r22 | r2m | ||
| . . . n | . . . rn1 | . . . rn2 | . . . rnm | |
| рангов | r1 | r2 | r |
В нижней строке табл. 1.4 записываются суммы рангов, полученные каждой продукцией (чем больше сумма, тем продукция важнее). Результирующее упорядочение продукций осуществляется согласно оценкам ri.
Статистическая согласованность (значимость) ранжирования проверяется для случая отсутствия равных рангов в ранжировке каждого эксперта, на основании коэффициента конкордации (согласованности) W:
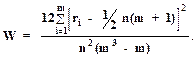 (1.39)
(1.39)
В случае нестрогого ранжирования (при наличии равных рангов) используется формула:
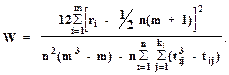 (1.40)
(1.40)
где k - число групп равных рангов, введенных i-м экспертом; t - число одинаковых элементов в j-ой группе i-го эксперта.
Пусть значение W найдено. Вычисляется величина n(m - 1)W, для которой задаются вероятностью ошибки Рош. Согласно c2 - распределения с (m - 1)степенью свободы для Рош находят табличное значение Wтаб. Если найденное значение W³Wтаб, то W считается статистически значимой.
Другой вариант извлечения знаний, связан с ответом системы на запросы пользователя. При этом вопрос интерпретируется как теорема, которая подлежит доказательству, а нахождение ответа на вопрос ищется на основании метода доказательства теорем. В рамках этой концепции построена система логического пропсам- минования Пролог, рассматриваемая позднее. В качестве иллюстрации рассмотрим следующий Пролог - подобный пример.
Здоровое_тело (Y) ® Здоровый_дух (Y).
Спортсмен (Х) & Ведет_здоровый_образ_жизни (Х) ® Здоровое_тело (Х).
Здоровый_дух (Z) ® Подходящий_партнер (Z).
Спортсмен (Сидоров).
Спортсмен (Иванов).
Спортсмен (Петров).
Здоровое_тело (Федоров).
Ведет_здоровый_образ_жизни (Петров).
Ведет_здоровый_образ_жизни (Сергеев).
Зададим вопрос системе в форме
? - Подходящий партнер (Т).
Для того, чтобы ответить на этот вопрос, система должна построить дедуктивную цепочку с чаключением в виде теоремы-вопроса. Не приводя способа построения этой цепочки, укажем ее Симу (одну ич подходящих цепочек):
Спортсмен (Петров) ® Ведет_здоровый_образ_жизни (Петров) ® Здоровое_тело (Петров) ® Здоровый_дух (Петров) ® Подходящий партнер (Петров).
Следовательно, ответом на вопрос является Т = Петров.
Дата добавления: 2016-03-05; просмотров: 998;
