Линейная резолюция в L
Определение. Для данного множества S дизъюнктов и дизъюнкта С0 из S линейный вывод дизъюнкта Сn из S с верхним дизъюнктом С0 - это вывод, изображенный на рис. 1, где
1) для i = 0, 1, ..., n-1 дизъюнкт Ci+1 есть резольвента дизъюнкта Сi и Вi; дизъюнкты Ci называется центральными Вi - боковыми.
2) Вi либо принадлежит S, либо есть Сj для некоторого j < i.Показано, что линейная резолюция является полной, т.е. для любого противоречивого множества дизъюнктов всегда выводится пустой дизъюнкт.
Дополнительное усиление рассмотренной стратегии предложено Лавлендом, Ковальским и Кюнером. Ими установлены условия, при которых центральный дизъюнкт позднее может участвовать в роли бокового дизъюнкта. Это свойство позволяет сократить число лишних дизъюнктов, поскольку становится ясно, будет или нет тот или иной центральный дизъюнкт использован для порождения пустого дизъюнкта. Прежде всего, множество литер произвольным образом упорядочивается, т.е. считается известным, какую литеру поставить левее в записи дизъюнкта, а какую правее. Например, пусть P > Q > R > 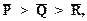 тогда считаем, что дизъюнкт PÚQÚ
тогда считаем, что дизъюнкт PÚQÚ 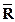 записан верно, а PÚ
записан верно, а PÚ 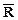 ÚQ- нет.
ÚQ- нет.
При порождении резольвент отсекаемая литера включается в представление резольвенты, но при этом указывается в рамке. Например, если
C1 = P Ú Q
C2 = 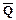 Ú R,
Ú R,
 то резольвента С1 и С2 имеет вид
то резольвента С1 и С2 имеет вид
P Ú Ú R.
Литеры в рамке служат для учета отрезанных литер: они не участвуют в дальнейшем порождении резольвент.
Рассмотрим дизъюнкт специального вида, в котором последняя литера не обрамлена и для этой последней литеры имеется контрарная обрамленная литера, например, Ú Ú 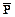 .
.
Дизъюнкт такого типа называется редуцируемым. Если С - редуцируемый дизъюнкт, то его можно сократить за счет отбрасывания последней литеры, а также всех обрамленных литер, за которыми не следует необрамленной литеры. Для редуцируемого дизъюнкта Ú Ú 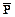 это сразу дает .
это сразу дает .
Следующая лемма формализует введенные определения.
Лемма. Если в некотором выводе С является редуцируемым упорядоченным дизъюнктом, то существует центральный упорядоченный дизъюнкт Cj (j<1), такой, что редукция Сi+1 дизъюнкта Ci является резольвентой Сi и Сj.
Доказательство. Если Сk и Сk+1, два соседних упорядоченных дизъюнкта на рис.7.1, то все литеры дизъюнкта Сk содержатся в Сk+1 (обрамленные литеры учитываются). Действительно, Сk+1 представляется как
|
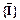 ),
),
где I - отсекаемая литера.
|
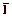 , где Р - некоторая дизъюнкция литер. Но тогда резольвентой Сi и P Ú
, где Р - некоторая дизъюнкция литер. Но тогда резольвентой Сi и P Ú 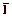 является Сi Ú P = Ci поскольку Р содержится в С.
является Сi Ú P = Ci поскольку Р содержится в С.
С учетом доказанной леммы упорядоченный вывод (называемый OL - выводом) определяется следующим образом:
1) Каждый дизъюнкт Вi либо принадлежит S, либо является ранее порожденным центральным дизъюнктом.
2) Если Сi редуцируемый упорядоченный дизъюнкт, то Сi+1 является результатом редукции Сi. В противном случае Сi+1 есть резольвента Сi и Вi, причем Вi принадлежит исходному множеству дизъюнктов и отсекаемая литера в Сi последняя.
3) В вывод не входят тавтологии.
Пример. Построим OL - вывод пустого дизъюнкта из множества дизъюнктов:
C1 = P Ú Q,
C2 = R Ú 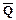 ,
,
C3 = R Ú 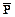
C4 = 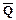 Ú
Ú 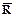
C5 = 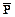 Ú
Ú 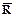 ;
;
P > Q > R > 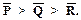
1. Находим резольвенту дизъюнктов С1 и С2, для которых отсекаемая литера последняя
|
2. Находим резольвенту дизъюнктов С6 и С4:
|
|
 .
.
3. Поскольку дизъюнкт С7 редуцируем, то сразу находим
С8 = Р
как результат редукции С7.
4. Находим резольвенту дизъюнктов С8 и С3:
|
5. Находим резольвенту С9 и С5:
|
|
 .
.
C10 является редуцируемым дизъюнктом. Следовательно, его редукция сразу дает
C11 = .
3.5.2.2 Метод линейного вывода в L Лавленда, Ковальского и Кюнера
Рассмотрим пример линейного вывода. Пусть дано

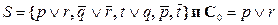
Введем дополнительные определения:
1. Входная резолюция – это применение правила резолюции, в котором одна из посылок – входной дизъюнкт (входная резолюция – это частный случай линейной резолюции).
2. Входным дизъюнктом является каждый член исходного множества S дизъюнктов.
3. Входной вывод – это вывод, в котором любое применение резолюции является входной резолюцией.
4. Входное опровержение – это входной вывод дизъюнкта ÿ из S.
5. Упорядоченный дизъюнкт – это последовательность различных литер. Это означает, что мы должны установить порядок всех литер в дизъюнкте. Примем соглашение, что литера L2 меньше, чем литера L1, в дизъюнкте С в точности тогда, когда L2 следует за L1 в последовательности, указанной в задании этого дизъюнкта. Таким образом, последняя литера всегда будет считаться наибольшей в дизъюнкте.
Уточним, что же предложили Лавленд, Ковальский и Кюнер.
Для этого рассмотрим пример. 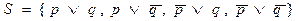 Здесь дизъюнкт p не является входным дизъюнктом. При этом легко видеть, что входное опровержение для исходного множества S отсутствует. Поэтому неизбежно использование одного из центральных дизъюнктов в качестве бокового. Однако, тогда возникает необходимость поиска необходимого и достаточного условия, при котором боковой дизъюнкт должен быть одним из ранее порожденных центральных дизъюнктов.
Здесь дизъюнкт p не является входным дизъюнктом. При этом легко видеть, что входное опровержение для исходного множества S отсутствует. Поэтому неизбежно использование одного из центральных дизъюнктов в качестве бокового. Однако, тогда возникает необходимость поиска необходимого и достаточного условия, при котором боковой дизъюнкт должен быть одним из ранее порожденных центральных дизъюнктов.
 Так вот, информация об отрезаемых литерах, записанная надлежащим образом, а также использование упорядоченного дизъюнкта дают возможность определить это условие. Уточним один важный момент - о записи отрезаемых литер.
Так вот, информация об отрезаемых литерах, записанная надлежащим образом, а также использование упорядоченного дизъюнкта дают возможность определить это условие. Уточним один важный момент - о записи отрезаемых литер.
Пусть С1 и С2 следующие упорядоченные дизъюнкты:
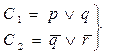
Результатом резолюции этой пары будет упорядоченный дизъюнкт – (p Ú r). При этом литеры q и 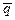 - контрарны, примем соглашение, что результат их дизъюнкции удалять не будем, а запишем его в виде одной левой литеры, обрамленной ее в рамку. Обрамленная литера – это отрезаемая литера, которая учитывается в дальнейших резолюциях следующим образом:
- контрарны, примем соглашение, что результат их дизъюнкции удалять не будем, а запишем его в виде одной левой литеры, обрамленной ее в рамку. Обрамленная литера – это отрезаемая литера, которая учитывается в дальнейших резолюциях следующим образом:
1. Обрамленную литеру должны выбрасывать только тогда, когда за ней не следует никакая необрамленная литера.
2. Если в упорядоченном дизъюнкте имеется более одного вхождение одной и той же необрамленной литеры, то всегда сохраняем самое левое вхождение, остальные совпадающие отбрасываем. Этот процесс называется отождествлением влево.
Перерисуем предыдущий пример


 Здесь дизъюнкт p Ú q Ú
Здесь дизъюнкт p Ú q Ú 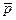 - редуцируемый дизъюнкт, который сразу дает пустой дизъюнкт.
- редуцируемый дизъюнкт, который сразу дает пустой дизъюнкт.
Это и есть необходимо и достаточное условие использования централизованного дизъюнкта в качестве бокового. В нашем случае это дизъюнкт р.
Применяя резолюцию дизъюнктов






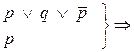
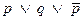
Все литеры в результате обрамлена, т.е. за ними не следует необрамленная литера, поэтому мы их удаляем все, в результате получаем пустой дизъюнкт, т.е линейное опровержение.  Порождаемые дизъюнкты типа называются редуцируемыми, их появление означает, что некоторый централизованный дизъюнкт нужно использовать в качестве бокового.
Порождаемые дизъюнкты типа называются редуцируемыми, их появление означает, что некоторый централизованный дизъюнкт нужно использовать в качестве бокового.
 Пример:
Пример: 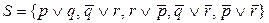
Дата добавления: 2016-03-05; просмотров: 1685;
