Доказательство высказываний, относящихся к программам дня вычислительных машин

Иногда не совсем ясно, доказываем ли мы справедливость S(N) для всех N, удовлетворяющих условию п₀ £п£M₀ или условию п₀ £п. В такой ситуации можно добиться успеха, даже и не зная, с каким из случаев имеем дело. Например, при доказательстве правильности программы иногда необхо­димо доказать справедливость некоторого высказывания S в те моменты, когда выполнение программы достигает неко­торой определенной точки. Можно попытаться доказать это методом индукции по п – числу «проходов» через данную точку программы. Однако мы можем и не знать точно, сколько раз проходим через эту точку: это зависит от данных, исполь­зуемых при выполнении программы. Мы можем проходить через нее и конечное (M₀), и бесконечное число раз (если программа не заканчивается из-за ошибки). Таким образом, можно попытаться доказать справедливость S(N) для N, удовлетворяющих условию 1£п£M₀ или условию 1£п. В любом случае мы можем получить результат, не зная, с каким вариантом мы имеем дело. Мы убеждаемся в справед­ливости S(N) при каждом проходе через определенную точку, если можем:

1. Доказать, что справедливо S(1), т. е. справедливо высказывание S при первом проходе через точку.

2. Доказать, что если справедливо S(N) (т. е. при N-ом проходе через точку), то справедливо и S(N+1), если мы, конечно, попадем в точку в п+1-й раз.

Если мы проходим через точку только т₀ раз, то значения N, для которых второе положение, возможно, справедливо, это те значения N, при которых мы п₀£п£M₀–1. Если же мы проходим через точку бесконечное число раз, то значения N, для которых может быть справедливо второе положение, это значения, удовлетворяющие условию 1£п. Таким образом, если мы докажем оба положения, то тем самым с помощью простой восходящей или простой индукции мы докажем справедливость высказывания S(N) для всех требуемых значений п вне зависимости от того, какой вариант встречается в действительности.

Глава 2. ДОКАЗАТЕЛЬСТВО ПРАВИЛЬНОСТИ БЛОК-СХЕМ ПРОГРАММ

Введение

При составлении программы для вычислительной машины мы стремимся к тому, чтобы программа решала некоторую определенную задачу. Однако каждый программист отчетливо и с горечью осознает, что большинство наших программ содержит ошибки. Мы тратим обычно много времени на тестирование и отладку созданных нами неправильных про­грамм. Даже закончив тестирование и отладку программы, мы не можем быть уверены, что она совершенно правильна. Все, что можно сказать о ней, это то, что программа дает правильные результаты для тех частных данных, которые использовались при ее тестировании. Позже, когда программа будет работать с новыми исходными данными, могут обна­ружиться и другие ошибки. Каждый опытный программист знает, что программа в течение долгого периода может рабо­тать без ошибок, кажется совершенно правильной, и вдруг внезапно, таинственным образом появляется очередная ошибка. Поэтому независимо от интенсивности тестиро­вания никогда нельзя поручиться за правильность программы.

Было бы идеально, если бы мы могли доказать правиль­ность программы, а не ссылаться только на проведенное тестирование. Конечно, если даже удастся доказать, что программа правильна, то нельзя быть в этом абсолютно уверенным. В доказательстве, как и в программе, также могут быть ошибки. Тем не менее, усилия, затраченные на доказательство правильности программы, способствуют всестороннему пониманию программы. Ведь чтобы доказать, что программа правильна, надо очень хорошо в ней разо­браться. Опыт показывает, что именно поэтому доказа­тельство правильности весьма полезно и способствует обна­ружению тех ошибок, которые могли быть пропущены, если бы доказательство не проводилось.

Если бы можно было формализовать доказательство пра­вильности и проводить его абсолютно надежным образом (автоматически доказывающим устройством), то ему можно было бы полностью доверять. В будущем это, возможно, окажется реальным, но не сейчас. Мы рассмотрим лишь неформально построенные доказательства правильности. Опыт проведения таких доказательств показывает, что при этом возрастают наша уверенность в программе и ее понимание, и поэтому доказательства следует выполнять, хотя они и не приводят к полной гарантии от ошибок. Неформальное доказательство правильности можно рассма­тривать как некоторую форму систематической проверки программы за столом, без машины, т. е. того, что всегда делает хороший программист. В этой главе даны основные идеи такого доказательства правильности для программ, пред­ставленных блок-схемами.

2.2. Основные принципы доказательства
правильности для блок-схем

Если мы хотим доказать, что некоторая программа правильна или верна, то прежде всего должны уметь описать то, что по предположению делает эта программа. Назовем такое описание высказыванием о правильности или просто утверждением. В этом случае доказательство правильности состоит из доказательства того, что программа, будучи запущенной, в конце концов окончится (выполнится оператор STOP), и после окончания программы будет справедливо утверждение о правильности. Часто требуется, чтобы программа работала правильно только при определенных значениях входных данных. В этом случае доказательство правильности состоит из доказательства того, что если программа выполняется при соответствующих входных данных, то она когда-либо за­кончится, и после этого будет справедливо утверждение о правильности.

Проиллюстрируем эти идеи на примере доказательства правильности для блок-схемы очень простой программы.

ПРИМЕР 1. Предположим, что нужно вычислить произ­ведение двух любых целых чисел M, N, причем M³0 и операцию умножения использовать нельзя. Для этого можно использовать операцию сложения и вычислить сумму из M слагаемых (каждое равно N). В результате получим M • N. Рассмотрим блок-схему, реализующую такое вычисление (рис. 2.1). Нужно доказать, что приведенная программа правильно вычисляет произведение двух любых целых чисел M и N при условии M³0, т. е. если программа выполняется с целыми числами M и N, где M³0, то она в конце концов окончится (достигнув точки 5)со значением J=M×N.

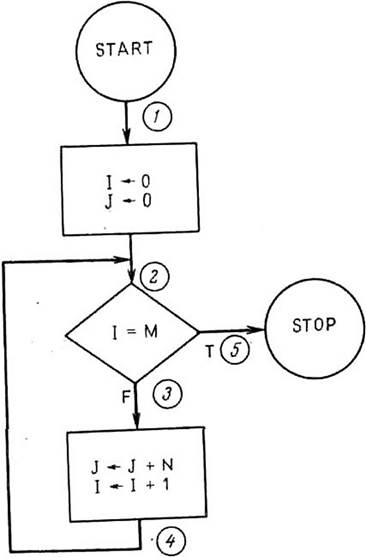
Рис. 1

Чтобы удостовериться в правильности работы блок-схемы, можно было бы проверить ее с некоторыми фиксированными данными. Например, давайте «вручную» промоделируем выполнение программы с числами M = 3 и N = 5. Ниже приведены значения переменных I и J в моменты достижения точки 2 на блок-схеме (вход в цикл):

Число проходов п через точку 2 Значение I Значение J

при выполнении блок-схемы

1 0 0

2 1 5

3 2 10

4 3 15

Когда мы в четвертый раз дойдем до точки 2, значение I будет равно 3, т.е. равно M, поэтому выполнение цикла закончится и мы попадем в точку 5.

При попадании в точку 5 переменная J=15=3×5. Таким образом, мы убеждаемся, что при M=3 и N=5 блок-схема работает верно. Хотя это, конечно, и укрепляет нашу уверенность в правильности работы программы, но тем не менее никак не доказывает, что программа будет работать правильно при всех возможных значениях M и N. Можно продолжать проверять программу с другими значениями M и N. Если для некоторых значений M и N будет получен неверный ответ, то надо еще узнать, что он неверен. Однако, если мы даже будем продолжать получать правильные ответы, все равно не будем уверены, что такие ответы будут полу­чаться для любых возможных значений M и N. Всегда остается бесконечное число возможных значений, для которых программа еще не проверялась. Конечно, если речь идет о неко­торой конкретной машине, то значение M и N ограничены некоторым конечным интервалом для целых чисел. В принципе в этом случае можно провести исчерпывающую про­верку с числами в этом интервале. Однако для большинства машин этот интервал настолько велик, что проводить исчер­пывающую проверку было бы не практично. Кроме того, мы составляем программу обычно таким образом, чтобы она работала верно независимо от размеров N и M. Следовательно, мы будем удовлетворены лишь тогда, когда сможем показать, что программа работает правильно независимо от размеров M и N. Методом тестирования мы этого никогда не достигнем.

Предположим, что вместо выполнения программы с конкретными значениями M и N мы начнем ее выполнять с символическими данными M и N. В этом случае мы получим следующую «трассу» для значений I и J при проходах через точку 2:

Число проходов Значение I Значение I

через точку 2

1 0 0

2 1 N

3 2

4 3 3×N

. . .

. . .

. . .

M+1 M M×N

Видно, что при выполнении цикла M раз (т. е. при M+1-ом попадании в точку 2) I = M, a J = M×N. Так как I=M, то мы покидаем цикл и попадаем в точку 5. Таким образом, при достижении точки 5 работа программы заканчивается и мы получаем J = M×N. Это показывает, что программа правильно работает для любых значений M и N. Однако отметим, что наша трассировка предполагает, что M³0, и поэтому значение I в конце станет равным M (оно начинается с 0 и увеличивается на 1 при каждом прохождении цикла). Если M < 0, то цикл будет повторяться, а значение I никогда не станет равным M; следовательно, программа не сможет закончиться. Таким образом, блок-схема в действительности работает правильно только для M³0. При любых целых значениях M и N и при условии M³0, как это видно из проведенной трассировки, работа блок-схемы закончится с J = M • N.

Кроме того, отметим, что в таблице есть «пробел» (многоточие). Как определить, какие значения I и J должны стоять в таблице после этого пробела? И как мы можем быть уверены, что они именно такие? На первый вопрос можно ответить следующим образом: прослеживая работу по блок-схеме и заполняя первую часть таблицы, мы начинаем понимать, как изменяются значения I и J при каждом проходе через цикл (у нас есть «образ» этого изменения), и пользуемся этим пониманием для предсказания значений I и J в момент M+1-го попадания в точку 2. Что касается второго вопроса, то для полной уверенности требуется провести доказательство. Из таблицы следует, что всякий раз, когда мы попадаем в точку 2, имеем J = I×N. Попробуем доказать это методом индукции по N – числу проходов через точку 2 (см. главу 1, где имеется исчерпывающее объяснение такого индуктивного доказательства).

1. При первом попадании (N = 1) в точку 2 (сюда мы приходим из точки 7) имеем I = 0 и J=0. Утверждение J = I×N = 0×N = 0, таким образом, справедливо.

2. Предположим, что J = I×N справедливо при N-ом попадании в точку 2. Нужно показать, что если мы попадем в точку 2 в N+1-й раз, то утверждение J=I×N опять будет справедливо. ПустьI и J при N-ом проходе через точку 2 принимают значения I_N и J_N. Тогда гипотеза индукции есть J_N=I_N×N. Единственный способ вновь попасть в точку 2 – выполнить тело цикла (точнее, пройти «по петле»), пройдя через точки 3, 4 и возвратясь опять в точку 2. Если это именно так, то, однажды проследив выполнение тела цикла, мы видим, что при возвращении в точку 2 новое значение I равно предыдущему значению плюс 1, а новое значение J – предыдущему значению плюс N. Таким образом,

I_N+1 = I_N + 1 и J_N+1 = J_N + N,

J_N+1 = I_N×N + N = (I_N + 1) × N = I_N+1 × N.

(По гипотезе

индукции)

Следовательно, если мы вновь попадем в точку 2 вп N+1-й раз, то J = I×N. Доказательство по индукции на этом заканчивается, и мы видим, что при любом попадании в точку 2 справедливо утверждение J = 1 • N.

Единственный способ закончить выполнение программы (перестать выполнять тело цикла) – попасть в точку 2 при справедливом условии I = M. В этот момент J = I • N = M • N, так как I = M. Дальше мы попадем в точку 5, и работа закан­чивается с J = M×N. Отметим, однако, следующее: мы еще не показали, что выполнение действительно закончится. Мы доказали только, что при каждом попадании в точку 2 справедливо утверждение J = 1 • N, и если выполнение когда-либо закончится, то J = M • N. Точнее, доказательство того, что J = I • N при каждом проходе через точку 2 не зависит от того, будет ли M³ 0 или нет. Следовательно, даже если M < 0, то доказательство останется корректным и подтверждает справедливость утверждения J=I×N при каждом попадании в точку 2. Но если M < 0, то цикл выполняется «бесконечно», так как I никогда не достигает значения M. Таким образом, выполнение программы никогда не закончится, и значение J = MN нельзя вычислить правильно. Однако даже в этом случае всякий раз при достижении точки 2 будет сграведливо утверждение J=I×N (если это не так, то наше предыдущее доказательство неверно). Справедливость этого можно проверить, проследив за работой программы с каким-нибудь значением M < 0: работа не кончается, но утверждение J = I • N в точке 2 всегда будет справедливым.

Следовательно, необходимо еще доказать, что выполнение программы закончится. Для этого следует предположить, что M³0. Итак, надо доказать, что если M³0, то в конце концов при выполнении программы мы попадем в точку 2 с I=M. Это утверждение очевидно: оно следует из блок-схемы программы. Действительно, в начале работы I присваивается значение 0, а затем при каждом проходе через цикл значение увеличивается на 1. Если учесть, что M – целое число и больше или равно 0, то очевидно, что I «дорастет» до M. Однако, чтобы получить более строгое доказательство, используем метод индукции.

Докажем с помощью восходящей индукции по M – переменной, удовлетворяющей условию 0£M£M, – что мы когда-нибудь достигнем точки 2 с I=M.

1. При первом попадании в точку 2 имеем I=0, т. е. утверждение справедливо для M=0. Если M=0, то это уже обеспечивает конечный результат.

2. В противном случае предположим, что мы в конце концов попали в точку 2 и I=M при 0£M£M. Требуется показать, что мы попадем в точку 2 и с I=M+1. В точке 2 с I=M и 0£M£M отношение I = M ложно, так как M < M, и, следовательно, мы пройдем по циклу и вернемся в точку 2. При таком возврате значение I увеличится на 1, т. е. очевидно, что мы попадем в точку 2 со значением I = M + 1, что и требовалось доказать.

Из изложенного выше можно заключить, что если М0, то в конце концов мы достигнем точки 2 с I=M. В этот момент отношение I=M истинно, и мы попадаем в точку 5, где работа программы заканчивается.

Итак, мы доказали (даже слишком подробно), что при выполнении нашей программы с заданными целыми M и N и условием M³0 выполнение ее в конце концов закончится, и при этом мы получим J =M • N.

ПРИМЕР 2. Мы провели предыдущее доказательство более подробно, чем это фактически необходимо. Повторим это доказательство, опуская некоторые детали и формаль­ности доказательства по индукции. В частности, доказывая справедливость некоторого высказывания в момент прохож­дения через какую-либо из точек внутреннего цикла (как это было в предыдущем примере), мы будем считать, что для этого нужно лишь показать, что: 1) высказывание справедливо при первом попадании в эту точку, и 2) если мы попали в эту точку и в этот момент высказывание справедливо, а затем выполняется цикл и мы вновь возвращаемся в исходную точку, то высказывание будет вновь справедливо. (то есть проще, выполнение цикла не нарушает истинности высказы­вания – инварианта цикла.) Если мы доказали оба этих утверждения, то, восстанавливая необхо­димые детали, можем доказать с помощью индукции по числу прохождений через точку, что исходное высказывание справедливо при любом попадании в данную точку. Приводя второй вариант этого доказательства правильности, мы будем «приписывать» ключевые утверждения, которые необходимо доказать, непосредственно тем точкам блок-схемы, к которым они относятся. Это поможет яснее представлять нам этапы доказательства правильности.

Докажем теперь, что приведенная на рис. 2.2 блок-схема правильна, т. е. если ее начать выполнять с M и N, имею­щими некоторые целые значения, причем M³0, то выпол­нение в конечном итоге закончится с J = M • N.

Вначале докажем, что при попадании в точку 2 J=I•N.

1. При первом попадании в точку 2 при переходе из точки 1 имеем I=0 и J=0. Таким образом, утверждение J = I•N = 0•N = 0 справедливо.

2. Предположим, что мы попали в точку 2 и утверждение J = I • N справедливо. Пусть I и J в этой точке принимают значения I_N и J_N, т.е. J_N = I_N• N. Предположим теперь, что мы прошли по циклу (от точки 2 через точки 3, 4 вновь в точку 2). При возвращении в точку 2 I и J принимают новые значения I_N+1 и J _N+1, которые можно представить следующим образом:

I_N+1 = I_N + 1,

J _N+1 = I_N• N+ N = (I_N + 1) • N = I_N+1• N.

(Так как J_N = I_N• N)

Следовательно, при очередном попадании в точку 2 высказы­вание J=I• N вновь справедливо, что и требовалось доказать, т. е. при любом попадании в точку 2 справедливо высказыва­ние J = I • N.

Теперь докажем, что в конце концов попадем в точку 2 со значением I=M. При первом попадании в точку 2 имеем I=0. При последующих попаданиях, если таковые есть, I каждый раз увеличивается на 1. Так как значение M нигде в программе не изменяется и мы предположили, что M³0, то очевидно, что в какой-то момент I станет равным M.

Если мы попадем в точку 2 при I = M, то будет верно и J = I • N = M • N. Отношение I = M в этот момент истинно, и мы попадаем по стрелке с пометкой Т (TRUE – истина) в точку 5 с J = M • N. На этом доказательство правильности программы заканчивается.

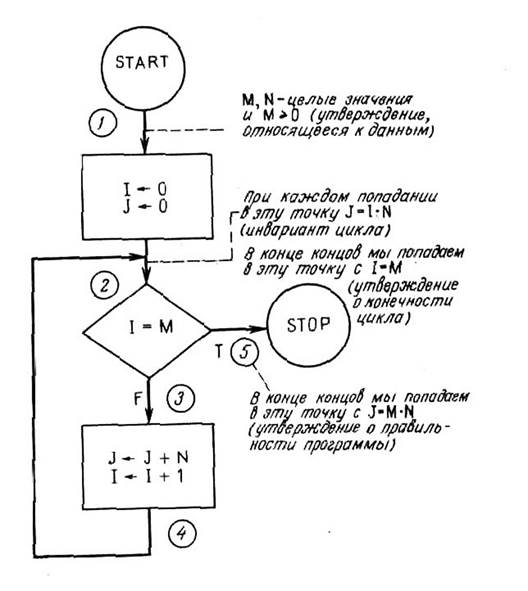
Рис. 2.

ПРИМЕР 3. Докажем правильность программы вычисления целого частного IQ и остатка IR от деления J1 на J2, где J1 и J2 – любые два целых числа, удовлетворяющие условиям 0 £ J1 и 1 £ J2. Операция деления в программе для вычисления IQ и IR не используется. Один из способов указать, что делает программа, – сказать, что она вычисляет два целых числа IQ и IR, таких, что J1 /J2 = IQ + IR/J2 и 0 £ IR < J2. Это можно записать так: J1 = IQ • J2 + IR и 0£IR<J2. Как и выше, свяжем непосредственно с блок-схемой программы
(рис. 3) допущения о входных данных и те утверждения, правиль­ность которых требуется доказать.

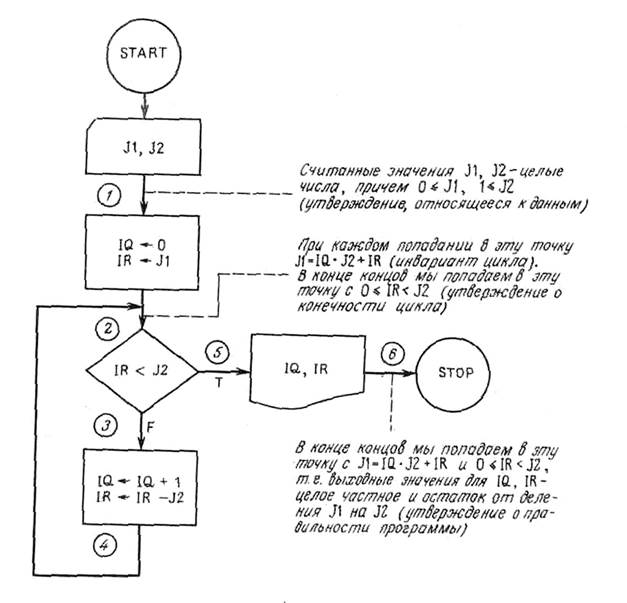рис. 3.

Отметим, что допущения о считываемых значениях для J1 и J2 мы поставили непосредственно после ввода. Это ука­зывает на то, что правильность работы программы будет доказываться только для данных, удовлетворяющих этому допущению. Утверждение о правильности блок-схемы связано с ее последней точкой. Кроме того, с начальной точкой цикла связываются два основных факта, которые требуется доказать. Теперь проследим за работой программы с символическими данными для J1 и J2 и выясним, как ведут себя инварианты цикла (основные утверждения о цикле):

Число проходов Значение IQ Значение IR

через точку 2

1 0 J1

2 1 J1 – J2

3 2 J1 – 2 • J2

4 3 J1 – 3 • J2

. . .

. . .

. . Пока IR < J2

Отметим, что при каждом попадании в точку 2

IR = J1 – IQ • J2,

или

J1 = IQ • J2 + IR.

Это утверждение идентично утверждению о правильности, за исключением того, что последнее еще включает условие 0 £ IR < J2. Таким образом, остается лишь показать, что цикл когда-нибудь закончится и при этом будет выполняться условие 0 £ IR < J2. Легко установить, что высказывания, связанные с точкой 2, утверждают именно эти факты о цикле.

Для доказательства правильности программы сначала по­кажем, что, как только мы попадем в точку 2, J1 = IQ • J2 + JR.

1. При первом проходе через точку 2, двигаясь от точки START к точке 2, имеем IQ = 0 и IR = J1, т. е. утверждение

J1 = IQ • J2 + IR = 0 • J2 + J1 = J1

справедливо.

2. Предположим, что выполнение программы дошло до точки 2 и справедливо утверждение J1 = IQ • J2 + IR. Пусть IQ и IR в этот момент принимают значения IQ_N и IR_N. Наше справедливое по предположению утверждение запи­сывается так: J1 = IQ_N • J2 + IR_N (гипотеза индукции). Пройдем один раз по циклу (от точки 2 через точки 3, 4 опять в точку 2). При возвращении в точку 2 новые значения IQ и IR будут такими: IQ_N+1 = IQ_N + L и IR_N+1 = IR_N – J2. Таким образом,

IQ_N+1 • J2 + IR_N+1 = (IQ_N + 1) • J2 + (IR_N – J2) =

IQ_N •J2 + J2 + IR_N – J2 = IQ_N •J2 + IR_N = J1,

(По гипотезе индукции)

Что и требовалось доказать, т. е. при попадании в точку 2 справедливо высказывание J1 =IQ • J2 + IR.

Теперь докажем, что в конце концов мы попадем в точку 2 при условии 0 £ IR < J2. Для этого покажем вначале, что при всяком проходе через точку 2 имеем 0 £ IR.

1. При первом проходе через точку 2 имеем IR = J1 и по предположению 0 £ J1. (Отметим, что это единственное место в доказательстве, где используется данное предположение. Таким образом, если бы мы не потребовали IR³0, то блок-схема должна была бы работать правильно даже для отрица­тельных значений J1.)

2. Предположим, что мы попали в точку 2 и 0 £ IR. Пусть в этот момент IR принимает значение IR_N. Если мы через цикл вернемся вновь в точку 2, то IR примет новое значение IR_N+1 =IR_N – J2. Но через цикл мы пройдем только в случае отрицательного ответа на проверку IR_N < J2, т. е. если истинно отношение J2 £ IR_N. Но если J2 £ IR_N, то 0 £ IR_N – J2 = IR_N+1 истинно. Таким образом, мы доказали, что 0 £ IR при каждом попадании в точку 2.

Докажем затем, что в конечном итоге мы попадем в точку 2 при справедливом условии IR < J2 (т. е. в этом случае мы будем иметь 0 £ IR < J2). Отметим, что при каждом про­ходе через цикл значение IR уменьшается на значение J2. Так как значение J2 в программе нигде не изменяется и так как 1 £ J2, то, очевидно, при каждом повторении процесса IR уменьшается по крайней мере на 1. Следовательно, в конце концов значение IR должно стать меньше J2 (с помощью метода индукции это можно доказать более строго).

Таким образом, в какой-то момент мы попадем в точку 2 со справедливыми условиями 0 £ IR < J2 и J1 =IQ • J2 + IR. В этот момент условие IR<J2, естественно, истинно, и из точки 2 мы идем в точку 5, а затем в точку 6. Так как на пути из точки 2 в точку 6 ни одна переменная не изменяется, то очевидно, что в момент прихода в точку 6 утверждение о правильности будет справедливо. Следовательно, мы доказа­ли, что при выполнении программы с целыми J1 и J2, удовлетворяющими условиям 0 £ J1 и 1 £ J2, программа в какой-то момент закончится, и будут справедливы отношения J1 = IQ • J2 + IR и 0£IR<J2, т, е. IQ и IR будут целыми частным и остатком от деления J1 на J2.