Глава 1. Индукция в научном познании

В процессе мышления и познания повсеместно используются две процедуры, которых кратко мы уже касались выше, - это индукция и дедукция. Ниже мы остановимся на этих процедурах более подробно. Во-первых, следует отметить, что индукция и дедукция могут выступать в научном познании двояко – как методы и как логические выводы. В качестве методов, они выступают правилами научной деятельности отдельного ученого или целого научного сообщества. В форме логических выводов, эти процедуры выражают себя как правила и нормы мышления – одной из активностей познающего субъекта. Ниже мы в первую очередь дадим характеристику индукции и дедукции как логических выводов, понимая здесь термин «логика» в широком смысле – как единство индуктивной и дедуктивной логики.

Обычно выделяют два основных смысла понятия «индукция»: 1) индукция как обобщение (назовем это понимание индукции индукцией-1), 2) индукция как вероятностный вывод (индукция-2). В общем случае эти виды индукции не исключают друг друга, поэтому точнее говорить о следующих трех видах индукции: 1) индукция как обобщение, являющееся достоверным выводом (индукция-1 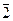), 2) индукция как обобщение и вероятностный вывод (индукция-12), и 3) индукция как вероятностный вывод, не являющийся обобщением (индукция- 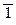2).

Ниже мы остановимся на характеристике следующих видов индукции:

- Математическая индукция

- Перечислительная (энумеративная) индукция

- Элиминативная индукция

- Индукция как обратная дедукция

- Аналогия

- Логическая индукция

§ 1. Математическая индукция

Это вид индукции-1 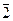, т.е. индукция как обобщение, являющаяся достоверным (не вероятностным) выводом. Степень достоверности этого вида вывода казалась ряду мыслителей столь значительной, что предлагалось даже рассматривать математическую индукцию как одну из аксиом формальной логики.

Самым простым видом математической индукции является индукция на множестве натуральных чисел. Предположим, что нам нужно доказать, что все натуральные числа, т.е. числа 1, 2, 3, 4, … , обладают некоторым свойством Р. Чтобы доказать это, мы, согласно аксиоме математической индукции, должны доказать следующее:

1) доказать, что свойство Р верно для единицы 1 (этот шаг носит название базис индукции),

2) предположив, что свойство Р верно для натурального числа k, мы должны на этой основе суметь доказать, что свойство Р верно для числа (k+1) (этот шаг получил название индуктивное предположение).

Если нам удается доказать эти два пункта, то мы можем быть уверены, что свойство Р верно для всех натуральных чисел. В самом деле, в этом случае свойство Р верно для 1. Но если оно верно для 1, то, согласно второму пункту, оно верно для 2. А если верно для 2, то верно и для 3. Если верно для 3, то верно и для 4…, и так далее – верность свойства Р побежит по всей бесконечной цепочке натуральных чисел, охватив их все.

Приведем простой пример применения математической индукции. Пусть, например, нам нужно доказать, что (n+1 > n) – последующее натуральное число больше предыдущего. Для доказательства этого свойства, кроме аксиомы математической индукции, будем использовать две такие аксиомы:

(А1) 2 > 1 – два больше единицы

(А2) Если (n > m) и k – любое натуральное число, то n+k > m+k – прибавление числа к обеим частям неравенства не меняет знака неравенства.

Итак, чтобы теперь доказать, что для любого натурального числа n верно свойство (n+1 > n), мы должны доказать базис индукции и индуктивное предположение:

1) базис индукции мы получим из (n+1 > n) при n=1. Это как раз 2 > 1 – наша первая аксиома (А1).

2) индуктивное предположение выражается, во-первых, в допущении, что для натурального числа k свойство выполнено, т.е. (k+1 > k). Теперь, исходя из этого, нам нужно попытаться доказать, что свойство (n+1 > n) верно для n=k+1. При n=k+1 получим, что (n+1 > n) выглядит как ((k+1)+1 > k+1), т.е. как результат прибавления единицы к обеим частям неравенства (k+1 > k), которое мы считаем верным. Следовательно, верным при этом предположении будет и свойство ((k+1)+1 > k+1), согласно второй аксиоме (А2).

Отсюда, согласно аксиоме математической индукции, мы делаем вывод, что свойство (n+1 > n) верно для любого натурального числа.

При таком применении математической индукции есть ряд тонкостей, которые необходимо иметь в виду.

Во-первых, вывод по индукции в этом случае использует понятие переменной n или k по натуральным числам. Переменная – это особый объект, который представляет собой любой конкретный объект и в то же время ни один из этих объектов в частности. Переменная – это именно переменная, т.е., например, переменная n – это и 1, и 2, и 3, и 4, …, но в то же время это и не 1, не 2, не 3, не 4, … . Это общее имя любого натурального числа, обозначающее любое из них, но ни одно в особенности. Переменная замечательна тем, что все то, что мы говорим через переменную, можно сказать о любом конкретном объекте, обозначаемым этой переменной. Например, если верно вообще, что (n+1 > n), то верно, в частности, что (4+1 > 4) или (17+1 > 17). Работая с переменной, мы как бы работаем с тем бесконечно общим, что есть во всех натуральных числах. В этом смысле идея переменной очень важна для научного познания, она как бы концентрирует в себе бесконечность множества индивидуальных объектов. Каждый такой объект, например, числа 1,2,3,…, называются частными значениями переменной. Хотя переменная обобщает нечто во всех своих частных значениях, но сама она продолжает быть обобщенной единичностью – как бы типичным представителем всех индивидуальных объектов. С этой точки зрения переменная не есть и просто общее, но скорее – общая единичность, т.е. общее во всех единичных объектах, но сохраняющая в себе существование как тоже некоторая единичность. Переменная не превращается в общее качество индивидуальных объектов, существующее само по себе и вне этих объектов, как, например, общее качество «быть натуральным числом». Нет, переменная сохраняется как объект вместе с индивидуальными объектами - как объект-общее всех этих частных объектов. Мы как бы вырезаем из всех индивидуальных объектов их общую часть и даем ей существование как самостоятельному единичному объекту наряду с частными объектами – так возникает конструкция переменной, играющая столь важную роль в математике, логике и вообще научном познании.

Во-вторых, следует отличать индуктивное предположение в математической индукции от заключения индукции. Дело в том, что по форме они звучат очень похоже – как допущение некоторого свойства Р для переменной. Но здесь нужно иметь в виду, что в индуктивном предположении мы допускаем верность свойства Р для переменной в условной форме: мы не говорим просто, что Р верно для переменной, мы утверждаем, что если бы Р было верно для переменной, то Р было бы верно и для переменной плюс один. Такая формулировка не есть формулировка самой математической индукции («Р верно для переменной»), и эту тонкость необходимо иметь в виду, чтобы не считать, что в индукции заложена тавтология.

Теперь общую схему аксиомы математической индукции можно было бы изобразить в следующем виде:

Свойство Р верно для 1

Если свойство Р верно для n, то Р верно для (n+1)

Свойство Р верно для n

Над чертой стоят две посылки – базис и индуктивное предположение. Под чертой – заключение индукции. Мы видим здесь пример обобщения – от верности свойства Р для 1 и условной верности Р для пары «переменная n - переменная (n+1)» мы переходим к безусловной верности свойства Р для переменной, т.е. для любого натурального числа. Это обобщение не несет в себе вероятности, но считается достоверным выводом, подобным выводам в формальной логике. Такая особенность математической индукции связана с особой организацией того множества объектов – натуральных чисел, - на которых индукция осуществляется. Это множество линейно упорядочено, все объекты здесь выстроены в бесконечную цепочку, что и позволяет, благодаря такой регулярности, усилить индуктивные средства и добиться более надежного вывода о свойствах всех объектов бесконечного множества на основании поведения части этих объектов. Кроме того, как мы видели, важнейшую роль в индуктивном выводе играет понятие переменной как объективированного общего всех частных объектов.

В общем случае математическая индукция может использоваться не только на натуральных числах, но и на других множествах объектов, которые в этом случае носят название индуктивных множеств. Но во всех этих случаях присутствуют те же принципиальные моменты – базис и индуктивное предположение, иерархическая организация индуктивного множества, использование переменных и т.д., - которые возникают уже в простейшем случае на множестве натуральных чисел.

§ 2. Перечислительная (энумеративная) индукция

Выше мы уже рассматривали примеры этого вида индукции. Как отмечалось ранее, в индуктивном выводе мыслитель имеет дело с некоторым классом объектов. Этот класс содержит обычно очень большое число объектов, которые практически невозможно все исследовать. Далее обнаруживается, что некоторое конечное число объектов обладает некоторым свойством Р. На этом основании исследователь может с некоторой вероятностью предполагать, что свойство Р выполняется для всех объектов класса. Получаем следующую общую форму перечислительной индукции:

1-й объект о₁ класса К обладает свойством Р

2-й объект о₂ класса К обладает свойством Р

…

n-й объект о_n класса К обладает свойством Р

Все объекты класса К обладают свойством Р

Утверждения над чертой – посылки индукции, под чертой – индуктивное заключение. Обозначим множество всех объектов {о₁, о₂,…, о_n} через F. Множество F в общем случае является частью всего класса К. Здесь различают два следующих случая:

1) Класс всех объектов К исчерпывается множеством F, т.е. в посылках мы проверили обладание свойством Р для всех объектов класса К. Например, мы утверждаем свойство «быть младше 20 лет» для всех учеников некоторого класса. Если в классе, допустим, 17 человек, то для каждого из них мы можем определить возраст, установив, что он меньше 20 лет, а затем перейти к выводу «Все ученики класса младше 20 лет». Такой вид перечислительной индукции называется полной перечислительной индукцией, поскольку множество F здесь полностью исчерпывает собою исследуемый класс К. Это вид индукции является переходом от частного к общему, но не является вероятностным выводом, т.е. является индукцией-1 .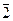

2) Класс всех объектов К не исчерпывается множеством F, например, К может быть бесконечным множеством, в то время как множество F всегда содержит только конечное число элементов. Этот вид индукции называется поэтому неполной перечислительной индукцией. Здесь мы уже совершаем скачок в мышлении, переходя от выполнения свойства Р на части класса К к выполнению этого свойства на целом классе К. Из-за такого скачка возможны ошибки, когда в оставшейся от F части К может найтись объект, который еще не проверен нами на обладание совйства Р и на самом деле таким свойством не обладает. Например, вы стоите на остановке и ждете автобуса № 3. В первый раз подошел автобус № 2 (Автобус № 3 не подошел в момент t₁), затем подошел автобус № 7 (Автобус № 3 не подошел в момент t₂), затем - № 1А (Автобус № 3 не подошел в момент t₃). В отчаянии вы уже готовы сделать индуктивный вывод «Автобус № 3 никогда не подойдет» (здесь в качестве объектов выступают моменты времени), и вдруг радостно замечаете, что из-за поворота наконец показался ваш долгожданный автобус № 3. Поэтому неполная перечислительная индукция – это в общем случае только вероятностный вывод. Но это несомненно обобщение, так что в целом получаем этот вид индукции как индукцию-12. Именно неполная перечислительная индукция представляет из себя наиболее типичный пример индуктивного вывода. Она, в свою очередь, может быть разделена на популярную и научную индукцию.

2.1) популярная неполная перечислительная индукция. Представляет из себя случай неполной перечислительной индукции, когда для обоснования индуктивного вывода не привлекается никаких дополнительных и серьезных аргументов. Обычно этот вид обобщения делается поспешно, под влиянием эмоций и в рамках обыденной жизни человека (подобно выводу «Автобус № 3 никогда не подойдет»), почему и носит название «популярной индукции».

2.1) научная неполная перечислительная индукция. Это, наоборот, случай неполной перечислительной индукции, когда привлекаются те или иные дополнительные средства обоснования индуктивного вывода из арсенала определенной научной теории. Например, биолог, изучая брачное поведение нескольких пар птиц, может обобщить свои наблюдения на все пары данного вида птиц. В этом случае в биологии используется гипотеза об однородности поведения всех особей одного вида, например, на основе анатомического и физиологического сходства этих особей. Здесь обобщение производится уже не столь произвольно, как в популярной индукции, но подкрепляется дополнительными научными средствами.

Оставшиеся виды индукции также представляют из себя случаи неполной перечислительной индукции, использующие те или иные средства своего дополнительного обоснования. В этом смысле они вполне могли бы быть рассмотрены как подвиды научной индукции, но обычно их рассматривают отдельно, в связи с типичностью и самостоятельной выделенностью используемых в них дополнительных методов обоснования индукции.

§ 3. Элиминативная индукция

Это вид неполной перечислительной индукции, в которой дополнительно используются попытки обоснования или опровержения ряда дедуктивных следствий нашего индуктивного заключения. Например, мы делаем индуктивное заключение, что «У всех больных гриппом болезнь вызвана вирусом гриппа». Кроме прямой проверки этого заключения в посылках индуктивного вывода

У 1-го человека б₁ класса больных гриппом Г болезнь вызвана вирусом гриппа

У 2-го человека б₂ класса больных гриппом Г болезнь вызвана вирусом гриппа

…

У n-го человека б_n класса больных гриппом Г болезнь вызвана вирусом гриппа

У всех больных гриппом болезнь вызвана вирусом гриппа

здесь могут дополнительно привлекаться методы опровержения заключения. Заметим, что заключение может быть записано в нашем примере в условной форме

«Если человек болен гриппом (Р), то у человека болезнь вызвана вирусом гриппа (Q)»

Здесь свойство Р – свойство «быть больным гриппом», свойство Q – «обладать болезнью, вызванной вирусом гриппа». Поэтому индуктивное заключение может быть записано в такой общей форме:

Если человек обладает свойством Р, то человек обладает свойством Q,

или еще короче:

Если Р(ч), то Q(ч),

где Р(ч) – человек обладает свойством Р,

Q(ч) – человек обладает свойством Q.

Из утверждения «Если Р(ч), то Q(ч)», согласно законам логики, вытекает инвертированное утверждение «Если не верно, что Q(ч), то не верно, что Р(ч)», т.е. в нашем случае это утверждение «Если болезнь не вызвана вирусом гриппа, то это не грипп (по симптомам)». Поэтому мы можем использовать дополнительную индукцию для обоснования нашей первоначальной индукции. Это будет индукция вида:

У 1-го человека б₁ класса больных, чья болезнь не вызвана вирусом гриппа 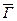, нет клиники гриппа

У 2-го человека б₂ класса больных, чья болезнь не вызвана вирусом гриппа 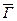, нет клиники гриппа …

У n-го человека б_n класса больных, чья болезнь не вызвана вирусом гриппа 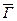, нет клиники гриппа

У всех больных, чья болезнь не вызвана вирусом гриппа, нет клиники гриппа

Чтобы опровергнуть утверждение «Если Р(ч), то Q(ч)», достаточно найти хотя бы одного такого человека ч₀, что он будет болен гриппом (Р(ч₀)), но в то же время будет доказано, что его болезнь не будет вызвана вирусом гриппа (не верно, что Q(ч₀)). Такой случай носит название контрпримера для утверждения «Если Р(ч), то Q(ч)». Если контрпример будет найден и доказан, то утверждение «Если Р(ч), то Q(ч)» уже не может быть верным и должно быть отброшено – элиминировано. Поэтому мы можем пытаться не только прямо подтвердить наше индуктивное заключение, но и поискать контрпримеры к нему. Если мы не найдем таких контрпримеров, то индуктивное заключение получит дополнительное подкрепление (кроме того, практически может оказаться, что обоснование примера «Если Р(ч), то Q(ч)» сложнее, чем неподтверждение контрпримера «Р(ч₀) и не верно, что Q(ч₀)»).

Единство неполной перечислительной индукции вместе с дополнительной индукцией инвертированных следствий (типа «Если не верно, что Q(ч), то не верно, что Р(ч)») или невозможностью найти контрпримеры (типа «Р(ч₀) и не верно, что Q(ч₀)») для основной индуктивной гипотезы (типа «Если Р(ч), то Q(ч)») и получило название «элиминативной индукции», в связи с широким применением приемов отрицания и элиминации в этой методике обоснования индуктивного заключения.

§ 4. Индукция как обратная дедукция

С перечислительной индукцией вида

Р(а₁)

Р(а₂)

…

Р(а_n)

Для любого х верно Р(х)

всегда связан обратный дедуктивный вывод такой формы:

Для любого х верно Р(х)

Р(а)

где а – какое-то частное значение переменной х. С точки зрения такого вывода индукция выглядит как переворачивание дедуктивного вывода, или – как обратная дедукция. Возможны случаи, когда индуктивный вывод дополнительно подкрепляется соответствующей ему обратной дедукцией. Правда, здесь может возникнуть вопрос: какой смысл состоит в том, чтобы сначала двигаться в мысли в одном направлении, а затем в прямо противоположном ? Ответ заключается в том, что движение в обратной дедукции может отличаться от просто противоположного направления движения в индукции в том случае, когда происходит возврат к таким частным значениям а, которых не было среди а₁, а₂, …, а_n. Например, Иоганн Кеплер мог бы использовать индукцию как обратную дедукцию, воспользовавшись наблюдениями Тихо Браге о движении планет и предположив, что планеты движутся по эллипсам. Рассуждения Кеплера в этом случае можно было бы представить, например, так.

Сначала множество частных наблюдений из таблиц Тихо Браге приводят к возникновению у Кеплера индуктивной догадки об эллиптичности планетарных орбит. Таблицы дают посылки индукции в форме утверждений «в момент времени t планета П находилась в месте пространства s». Точнее индукция могла бы выглядеть так:

В момент времени t₁ планета П находилась в точке эллипса s₁

В момент времени t₂ планета П находилась в точке эллипса s₂

…

В момент времени t_n планета П находилась в точке эллипса s_n

В любой момент времени t планета П находится в точке эллипса s(t)

Здесь происходит обобщение и по моментам времени t и по точкам пространства s. Поэтому в качестве объектов, по которым проводится обобщение, здесь выступают пространственно-временные координаты (s,t) положения планеты. От отдельных координат (s₁,t₁), (s₂,t₂), …, (s_n,t_n) в этом случае происходит переход к бесконечному множеству координат (s,t), где s – переменная, пробегающая все точки эллипса, t – переменная времени, пробегающая все моменты времени. Затем Кеплер мог обернуть индукцию, используя дедуктивный вывод

В любой момент времени t планета П находится в точке эллипса s(t)

В момент времени t* планета П находится в точке эллипса s*

и точка s* может в этом случае отличаться от всех имеющихся в посылках индукции точек s₁, s₂, …, s_n. Можно было бы проверить этот вывод в реальном наблюдении, и, если это наблюдение подтвердится, то мы получим дополнительное обоснование индукции.

Заметим, что в этом случае точка s* не могла бы быть получена из таблиц, в которых было фиксировано некоторое конечное число наблюдений. Поэтому индукция как обратная индукция обычно применяется и имеет смысл в тех случаях, когда первоначальное множество объектов, фигурирующих в посылках индукции, по тем или иным причинам ограничено, и обращение индукции позволяет здесь расширить это множество объектов, дополнительно подкрепив индукцию.

§ 5. Аналогия

В случае вывода по аналогии обычно даны два объекта и множество свойств (в отличие от перечислительной индукции, где дано одно или два свойства и множество объектов). Можно сказать, что перечислительная индукция – это обобщение по объектам, когда фиксируются свойства и изменяется множество объектов, а аналогия – обобщение по свойствам, когда, наоборот, фиксируются объекты и меняется множество свойств.

Рассмотрим следующий пример аналогии. Человек утверждает, что на Марсе есть жизнь, поскольку на Марсе, как и на Земле, есть атмосфера, вода, близкие к земным значения температур и силы тяжести. Такой вывод можно было бы представить следующим образом. Обозначим суждения

«Земля обладает атмосферой» - как А(з)

«На Земле есть вода» - как В(з)

«На Земле перепад температур в пределах DТ» - как Т(з)

«На Земле перепад силы тяжести в пределах DF» - как F(з)

«На Земле есть жизнь» - как Ж(з)

«Марс обладает атмосферой» - как А(м)

«На Марсе есть вода» - как В(м)

«На Марсе перепад температур в пределах DТ» - как Т(м)

«На Марсе перепад силы тяжести в пределах DF» - как F(м)

«На Марсе есть жизнь» - как Ж(м)

Тогда вывод по аналогии может быть представлен в следующей форме:

А(з), В(з), Т(з), F(з), Ж(з)

А(м), В(м), Т(м), F(м)

Ж(м)

Вывод по аналогии в общем случае может быть представлен в такой символической форме: есть два объекта о₁ и о₂, и множество свойств Р₁, Р₂, …, Р_n, P_n+1; в посылках устанавливается, что объект о₁ обладает всеми этими свойствами, а объект о₂ – первыми n свойствами. Тогда делается вывод, что о₂ обладает и (n+1)-м свойством. Таким образом, получим:

Р₁(о₁), Р₂(о₁), …, Р_n(о₁), Р_n+1(о₁)

Р₁(о₂), Р₂(о₂), …, Р_n(о₂)

Р_n+1(о₂)

Как и неполная перечислительная индукция, аналогия является вероятностным выводом, т.е. мы только с какой-то вероятностью можем предполагать наличие у второго объекта свойства P_n+1. Так же как и в случае неполной перечислительной индукции, можно было бы говорить о популярной и научной аналогии, в зависимости от того, подкрепляется ли аналогия какими-то дополнительными обоснованиями, или нет. Обычно дополнительное обоснование вывода по аналогии предполагает обоснование некоторой связи между свойствами Р₁, Р₂, …, Р_n и свойством P_n+1. Например, наличие жизни на планете с высокой вероятностью вытекает из определенных условий на этой планете (наличия атмосферы, воды и т.д.) в рамках абиогенной теории происхождения жизни, т.е. в предположении, что в результате различных метеорологических процессов в атмосфере могли синтезироваться органические соединения и возникнуть простейшие формы жизни.

§ 6. Парадокс лысого

Заканчивая этот раздел, посвященный индукции и ее видам, хотелось бы отметить, что проблема индукции как особой мыслительной операции до сих пор таит в себе множество неясностей и неоднозначностей. Некоторые философы, как например английский философ Карл Поппер, вообще отрицали индукцию как прием и метод научного познания. По-видимому, дело здесь в большом значении дополнительных методов обоснования, необходимых для полноценного использования индукции. Как мы видели, сама по себе индукция в чистом виде – в форме популярной индукции - вряд ли носит научный характер и всегда так или иначе должна подкрепляться еще чем-то. Необходимость в такого рода дополнительных подкреплениях индуктивного вывода и малая ясность общей логики их использования, по-видимому, и порождает повышенную проблемность индукции как логического вывода сравнительно с выводом дедуктивным.

Для иллюстрации проблемности даже, казалось бы, такого наиболее обоснованного ее вида, как математическая индукция, проинтерпретируем в ее терминах так называемый «парадокс лысого», известный еще со времен античной науки и философии.

Допустим, есть некий лысый человек, который применяет настолько замечательное лекарство против облысения, что оно каждый день прибавляет к его лысине по одному волосу. Перестанет ли в этом случае человек быть когда-нибудь лысым ? Кажется, что да. Если прибавлять каждый день по одному волосу, то рано или поздно лысина исчезнет и человек перестанет быть лысым. Но попробуем сформулировать это утверждение в форме математической индукции.

Пусть свойство Р – свойство «быть видимо лысым». Тогда Р(ч) есть утверждение «человек (ч) видимо лысый», т.е. лысый, если смотреть на его голову обычными глазами с некоторого расстояния. Пусть далее n – человек с числом волос на голове, равных числу n, которое добавилось к первоначальной лысине человека спустя n дней. Здесь мы можем доказать следующее:

1. Базис индукции: Р(1) – человек с одним волосом на голове видимо лыс. Это кажется очевидным.

2. Индуктивное предположение: пусть будет верно, что P(n), т.е., что человек с n числом волос на голове видимо лыс. Тогда ясно, что добавление одного волоса не сделает в этом случае человека видимо не лысым, т.е. верным будет и P(n+1). Следовательно, если P(n), то P(n+1) – мы доказываем индуктивное предположение.

Теперь, если мы принимаем аксиому математической индукции, мы обязаны сделать вывод: для любого n верно P(n), т.е. человек будет видимо лысым при любом числе волос у него на голове, что явно представляет из себя нелепицу!

Проблема здесь состоит в том, что состояние «быть видимо лысым» определяется особым состоянием количества – зрительно воспринимаемым числом волос, которое проявляет неоднозначные свойства, не вполне вписывающиеся в поведение обычных чисел.

В процессе прибавления волос и зрительного восприятия их массы есть некоторый момент, когда количество волос вот-вот готово появиться как некоторый зрительный образ, но еще таковым не является. Для простоты предположим, что таким свойством обладает некоторое конкретное число волос m. Тогда результат прибавления одного волоса к этому множеству начнет себя вести уже своеобразно. Число волос (m+1) будет готово впервые стать видимым, если его рассматривать с точки зрения одного волоса. В то же время это число волос зрительно не отличимо от числа волос m. Получается, что одно и то же число (m+1) может оцениваться как бы из двух точек отсчета – единицы и предшествующего числа m. Чтобы выразить различие этих состояний, обозначим через n¯k число n, рассматриваемое с точки зрения числа k (это число n, получаемое из числа k умножением на величину (n/k)). Тогда число (m+1) предстает в двух своих ипостасях – как (m+1)¯1 (с точки зрения единицы) и как (m+1)¯m (с точки зрения предшествующего числа). В первой ипостаси число волос (m+1) готово стать видимым. Если через В обозначить свойство видимости, то В((m+1)¯1). Во второй ипостаси число волос (m+1)¯m не отличается от числа волос m, которое невидимо, т.е. неВ(m). Это приводит к невидимости и (m+1)¯m, т.е. неВ((m+1)¯m). Итак, получаем, что число волос (m+1) в разных своих состояниях обладает противоположными свойствами – видимостью и невидимостью. Так можно пытаться использовать более сложные – относительные, или ипостасные, - сотояния количества (чисел). С этой точки зрения можно различать два вида математической индукции:

1. Безусловная математическая индукция. Формулируется для чисел, данных в состояниях n¯1. В таких состояниях числа рассматриваются относительно единицы, т.е. как бы с абсолютной (безусловной) точки зрения. Аксиома математической индукции приобретет такой вид:

Свойство Р верно для 1¯1

Если свойство Р верно для n¯1, то Р верно для (n+1)¯1

Свойство Р верно для любого n¯1

2. Условная математическая индукция. Этот вид индукции предполагает использование относительных (условных) состояний чисел n¯k, где k>1. Схема этой индукции может иметь, по-видимому, не единственный вид. Например, такой:

Свойство Р верно для 1¯1

Если свойство Р верно для n¯1, то Р верно для (n+1)¯n или не верно для (n+1)¯1

Найдется такое m, что свойство Р верно для любого n, где n ≤ m

В этом виде индукции мы уже не можем утверждать свойство Р для всех натуральных чисел, но только для некоторого начального отрезка множества натуральных чисел. Именно такого рода индукция необходима для разрешения парадокса лысого. Главное отличие ее будет состоять в более тонком и сложном представлении индуктивного предположения. Парадокс лысого может быть теперь представлен следующим образом:

1. Базис индукции: Р(1¯1) – человек с одним волосом на голове видимо лыс.

2. Индуктивное предположение: пусть будет верно, что P(n¯1), т.е., что человек с n числом волос на голове видимо лыс. Тогда может оказаться и так, что n – это то самое пороговое число m, начиная с которого возникает видимость числа волос. В этом случае добавление одного волоса не сделает человека видимо не лысым с точки зрения предшествующего числа волос, т.е. верным будет P((n+1)¯n), и в то же время сделает впервые видимо не лысым с точки зрения одного волоса, т.е. неР((n+1)¯1). В целом для числа волос n возникнет как бы «мерцание» то в состоянии видимости за счет оценки n с точки зрения абсолютной системы отсчета («от единицы»), то в состоянии невидимости за счет сравнения с предшествующим числом.

Теперь, если мы принимаем аксиому относительной математической индукции, мы можем сделать лишь тот верный вывод, что человек будет видимо лысым при любом числе волос у него на голове в рамках некоторого начального их числа, не более того.

Видимая противоречивость парадокса лысого, как теперь можно предположить, была связана с неразличением относительных состояний чисел и невозможностью выразить более тонкий процесс зависимости свойства от условных числовых определений. В результате индуктивное предположение относительной индукции оказалось неверно представленным как предположение безусловной индукции, что и привело к противоречию. В общем случае количество подобно цвету, который на одном фоне может сделаться сильнее, на другом – слабее. В количестве есть не только абсолютные, но и относительные определения, вносящие свой вклад в суммарное выражение этого количества.

Уже на этом примере читатель мог убедиться, сколь не проста и далека от своего окончательного разрешения проблема индукции.