Глава 2. Дедукция в научном познании

В отличие от индукции, похожей на дырявую трубку, по которой течет и теряется истинность, к дедукции, как уже отмечалось выше, обычно предъявляется требование полного переноса истинности от посылок к заключениям. В этом смысле дедукция всегда была символом наиболее строгих и обоснованных методов научного мышления. По аналогии с индукцией, о дедукции можно было бы говорить по крайней мере в двух основных смыслах – как о переходе от общего к частному (назовем этот вид дедукции дедукцией-1) и как о достоверном выводе (дедукция-2). Не всегда эти два понимания дедукции совпадают (случай совпадения видов дедукции как перехода от общего к частному и как достоверного вывода можно называть дедукцией -12), в связи с чем можно говорить о дедукции-1 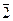- дедукции, являющейся переходом от общего к частному, но не представляющей из себя достоверного вывода, и о дедукции- 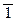2 – достоверном выводе, который, тем не менее, не является переходом от общего к частному.

По нашему мнению, однако, отличие дедукции от индукции во многом выражается сегодня в степени разработанности различных разделов логики. Индукция, как мы видели выше, таит в себе еще много неясного и проблематичного, это как бы менее разработанные, но активно развивающиеся сегодня разделы логики. Дедуктивная логика в этом смысле – это скорее наиболее разработанная часть логики вообще, которая исторически оказалась связанной с более простыми и базовыми логическими средствами мышления. С этой точки зрения мы будем придерживаться в этой главе не столько классификационного описания видов дедукции, что было бы более уместно в области, где еще отсутствуют глубокие теоретические обобщения, но попытаемся представить общий обзор дедуктивных методов познания как некоторых интегрированных систем мышления.

§ 1. Немного об истории дедуктивного познания

Основы дедуктивной логики были заложены еще в трудах древнегреческих философов и математиков. Здесь можно назвать такие славные имена, как имена Пифагора и Платона, Аристотеля и Евклида. Считается, что Пифагор одним из первых стал рассуждать в стиле доказательства того или иного утверждения, а не простого его провозглашения. В работах Парменида, Платона и Аристотеля сложились представления об основных законах правильного мышления. Древнегреческий философ Парменид впервые высказал ту замечательную мысль, что в основании подлинно научного мышления лежит некое неизменное начало («единое»), которое продолжает сохраняться неизменным, как бы не менялась точка зрения мыслителя. Платон сравнивает единое со светом мысли, который продолжает пребывать неизменным, пока есть сама мысль. В более строгой и конкретной форме эта идея получает свое выражение в формулировке основных законов логики у Аристотеля. Аристотель считается по праву основателем логики как дедуктивной науки. Он впервые систематизирует основные приемы правильного мышления, обобщая достижения современных ему древнегреческих математиков. В работах Евклида применение этих приемов и законов к математическим наукам достигает высочайшего уровня, который становится идеалом дедуктивного мышления на века и тысячелетия в европейской культуре. Позднее формулировки дедуктивной логики все более оттачиваются, детализируются у стоиков, в средневековой схоластике. Но это время практически не прибавляет ничего принципиально нового к сложившейся у Аристотеля и Евклида системе дедуктивного метода. И лишь с возникновением новой науки в 16-17 веках вновь начинается переосмысление и развитие античного наследия. Французский философ и математик Рене Декарт выдвигает понятие переменной, формулирует идею и правила дедуктивного метода как общего метода решения уравнений – суждений, содержащих переменные. Декарт подчеркивает значение очевидности (L-статуса) посылок и правил вывода в дедуктивных умозаключениях. Немецкий философ Готфрид Лейбниц выдвигает идею универсального дедуктивного метода, на основе которого мыслители были бы в состоянии прекратить бесплодные споры и перейти к строгому вычислению истинности или ложности выдвигаемых ими положений. В работах немецкого философа Иммануила Канта провозглашается замысел построения некоторой «трансцендентальной дедукции», способной выходить за границы законов формальной логики. Наконец, в конце 19 века в работах английского ученого Джорджа Буля строго формулируется идея логической переменной и логических уравнений, постепенно оформляется новая структура, составляющая алгебру мысли и получившая название «булевой алгебры» по имени своего первооткрывателя. В 20-м веке дедуктивная логика становится разделом математики и начинает называться «математической логикой». Основные идеи и методы дедуктивного подхода получают совершенно строгое выражение средствами языка математики. С этих пор начинается бурный рост математической логики как нового направления математического знания, получившего название «метаматематика».

§ 2. Искусственные и естественные языки

Такое бурное и успешное развитие дедуктивной логики привело к формулировке понятия формальной дедуктивной (аксиоматической) системы, к рассмотрению структуры которой мы ниже вкратце и обратимся. Дедуктивная система – это область мышления и языка, в высокой степени обработанная средствами дедуктивной логики и получающая в связи с этим некоторый законченный и организованный вид.

В первую очередь формальная дедуктивная система представляет из себя некоторый искусственный язык, специально приспособленный для описания определенной математической структуры. Вкратце мы уже касались некоторых идей, связанных с дедуктивными системами, в параграфе первой главы первого раздела, посвященного логическим теориям, описывающим структуры. Здесь будет сделан еще один шаг в направлении более подробного описания средств современной дедуктивной логики.

Очень часто учащихся и неспециалистов вводит в заблуждение термин «формальный» в применении к логическим языкам дедуктивной логики. Сегодня логика, как и математика вообще, во многом строится с применением множества специальных символов («значков»), которые кажутся бессмысленной абракадаброй несведущему человеку. Но в этом случае с равным успехом формальным можно называть, например, и язык нотной записи музыкальных произведений, который не менее понятен для непосвященного. Поэтому само по себе использование специального языка еще не означает чего-то обязательно «формального». Необходимо специально оговориться, в каком смысле искусственные языки логики и математики считаются формальными.

Под формальным можно понимать, по крайней мере, две вещи: во-первых, степень выражения в языковых средствах предмета языка (того, о чем говорит язык), во-вторых, степень общего, универсального, выражаемого языком. С первой точки зрения, обычные языки, например, русский, английский могут быть названы более формальными, чем язык математики. В самом деле, математический язык специально строится так, чтобы в структуре символов этого языка уже выражался предмет языка. Поэтому в математических языках форма и содержание языка гораздо более подобны друг другу, чем в языках обычных, и в этом смысле математические языки гораздо более содержательны. Вот почему можно порой работать с математическими знаками, не понимая их смысла (как это делается в компьютерах). Ведь уже в самой структуре математического знака заложен до некоторой степени закон его содержания. В разговорных языках на форму знаков (например, слов, букв) гораздо больше влияет природа пользователя этого языка, например, устройство гортани человека, позволяющей издавать фиксированный набор звуков. Поэтому в ненаучных языках больше разрыв между формой и содержанием знака, и в этом смысле они более формальны.

Во втором смысле, при понимании формальности как универсальности, конечно, более формальны математические языки. Они создаются для выражения очень общих и универсальных понятий и законов, в то время как обычный язык во многом порожден жизнью человека в близком ему опыте.

Искусственные языки науки и естественный язык взаимно дополняют друг друга. Искусственные языки более универсальны в своей области и обладают формой, более подобной своему содержанию. Однако искусственные языки практически ничего не могут сказать вне сферы своей компетенции, в то время как естественный язык способен сказать понемногу обо всем. Не надо думать, что можно было бы обойтись без искусственных языков, и их использование – результат лишь некоторого удобства. Есть много вещей, о которых либо вообще нельзя сказать, либо удается сказать очень приблизительно и неадекватно средствами естественного языка. В этом смысле овладение тем или иным искусственным языком – языком физики, математики, логики - оказывается во многом процессом приобретения нового органа понимания и выражения, этот момент нельзя недооценивать особенно в современном научном познании, насыщенном сложнейшими искусственными языковыми системами. Если различные естественные языки можно было бы называть синтаксическими (синтаксис – правила построения знаков языка), т.к. они различаются не столько смыслами, сколько звуковыми и письменными оболочками этих смыслов, в связи с чем давно возможен достаточно хороший перевод между такими языками; то разнообразие искусственных языков математики и других наук представляет из себя пример семейства семантических языков (семантика – наука об отношении знаков и их содержания), существенно различающихся системами выражаемых ими смыслов. Для перевода таких языков между собой необходим некоторый семантический гиперязык, способный объединить в себе смысловые пространства и подобные им знаковые формы различных искусственных языков. В наибольшей мере такой язык присутствует в современной математике, но, по-видимому, и его ресурсов пока существенно не хватает для переводов с языка одной частной науки на язык другой. Создание такого гиперязыка – это во многом проблема создания более универсального смысла, который еще отсутствует в современной науке. Другим возможным источником синтетического гиперязыка является философия, но до сих пор она слишком мало взаимодействовала с искусственными языками других наук, пытаясь максимально обходиться средствами естественного языка.

Одним из наиболее типичных примеров семантических языков как раз является искусственный язык современной дедуктивной логики.

§ 3. О законах формальной логики

В основе языка современной дедуктивной логики лежит некоторая первичная пара смыслов, которые носят название логический ноль (0) и логическая единица (1). Такая парность выражает фундаментальную природу человеческого разума, в основе которого лежит первичное деление на истину (1) и ложь (0). Что бы ни мыслилось разумом, оно всегда мыслится им как та или иная о-предел-енность, т.е. нечто, что имеет предел, границу. Но там, где граница, там есть и нечто, лежащее за границей – иное по отношению к первоначальной определенности. Следовательно, любой смысл в нашем сознании дан в паре со своим иным. Если обозначить смысл через Х, его иное – через неХ, то никогда нет просто Х, но всегда дана пара (Х,неХ), где Х лишь стоит на первом месте, но всегда соотнесен с неХ. Если так, то Х, начиная соотноситься со своим иным, тоже является парой, лишь усиленной на одном из своих элементов. Любой смысл парен, любая определенность дана как пара себя и своего иного. В этом – основа выразимости и мыслимости любой сущности. Выражая эту глубокую истину, логика и начинается с первообраза всех пар – пары (1,0). Это некоторое начало всякой мысли – пара «есть-нет», «истина-ложь», «данное-иное». Здесь как бы присутствует в сознании некоторый экран сознания Е, на фоне которого определяет себя любой смысл. Экран сознания подобен экрану в кинотеатре, на котором увлеченные зрители смотрят фильм в полной темноте. В этот момент для них существует лишь то, что существует на экране. Так и в сознании есть тоже как бы некий экран – экран сознания и внимания, - и существует для сознания в этот момент лишь то, что попадает в этот экран.

Парность выражает рассечение экрана на две части, что и порождает простейший смысл. Одна из этих частей притягивает к себе внимание, находится как бы в центре экрана (это 1). Оставшаяся часть уходит на периферию внимания и экрана, составляет как бы смысловой фон, контраст для определения первой определенности (это 0). В отношениях этих моментов рождаются и первые их отношения, позволяющие определить их именно таким образом.

Если есть две части экрана, то:

1) есть сам экран как их сумма. Возникает идея логической суммы (+) двух начал. Если первичную пару обозначать через (Х,У), то Е есть Х+У – экран есть сумма Х и У.

2) есть общее между двумя частями экрана, которая является результатом их единства, логического произведения (×). Обозначим это общее между Х и У через g(Х,У) (от англ. “general” - общий). Тогда g(Х,У) есть Х×У – общее есть логическое произведение Х и У.

3) есть переход от одной части к другой – операция логического перехода (обозначим ее через Т - символ трансформации). Тогда ТХ есть У и обратно: Т^-1У есть Х, где Т^-1 – переход, обратный к Т.

4) есть включение каждой части экрана в сам экран в целом – это операция логического следования, или импликации (ее обозначают обычно символом É). Здесь получим, что ХÉЕ и УÉЕ – Х и У включены в экран Е.

5) Наконец, может быть взаимное включение начал друг в друга, например, (ХÉУ) и (УÉХ). Такое взаимовключение, являющееся логическим произведением отдельных включений, называется логическим равенством или эквивалентностью (часто обозначается через º).

Итак, как только появляется первичная смыслопорождающая пара (Х,У), появляется и система описанных выше смыслоопределяющих операций. Все они являются элементами полной системы поддержания простейшей определенности в некотором экране сознания Е.

Что же такое основные законы дедуктивной (формальной) логики в этом случае ?

Их можно теперь продемонстрировать как некоторые условия, накладываемые на смысловую пару (Х,У) для определения ее в максимально первичном и различимом состоянии бытия. Результатом действия этих законов станет превращение неспецифической пары (Х,У) в максимально поляризованную и предельно резкую пару (1,0). Посмотрим с этой точки зрения на основные законы формальной логики.

1. Закон непротиворечия. Этот закон требует, чтобы общая часть g(Х,У) между полярными началами Х и У исчезла, обратилась в ничто. Тем самым они перестанут пересекаться и окажутся внешними друг другу.

2. Закон полноты (исключенного третьего). Этот закон можно рассмотреть как требование того, чтобы сумма начал Х и У исчерпала собой весь экран сознания Е, чтобы не было ничего третьего, что могло бы остаться в экране Е, кроме суммы Х и У.

Объединенное действие первых двух законов – закона непротиворечия и полноты – приводит к тому, что экран Е в точности разбивается парой Х и У на две несовместимые части.

3. Закон экстремальности (тождества). Этот закон выражает требование того, чтобы центральная (первая) определенность Х в паре (Х,У) распространила себя на весь экран Е, совпала бы с ним. Происходит абсолютизация Х, превращение ее в абсолютную истину. Равенство Х экрану превращается здесь в равенство Х самому себе, т.е. ХºХ.

Действие закона экстремальности вместе с первыми двумя законами приводит, как к своему следствию, к тому, что вторая – периферическая – определенность У в паре (Х,У) практически исчезает из экрана, превращаясь в его границу, в ноль бытия, в абсолютную ложность. Так пара (Х,У) окончательно переходит в пару (1,0), где логическая единица 1 есть совпавшая с экраном Е определенность Х, а логический ноль 0 выражает собою вторую определенность У как то ничто, которое вытеснено из экрана вообще. Совпадение Х с экраном Е вместо по крайней мере трех определенностей (Х, У и экран Е) приводит к возникновению только двух – единицы (она же - экран) и нуля. Поэтому в таком строго парном смысле возможны только две трансформации Т(1) º 0 и Т^-1(0) º 1. В логике используют один символ ù для этих трансформаций, называя операцию ù отрицанием. Так мы получаем в качестве еще одного следствия

4. Закон двойного отрицания: ùù1 º 1 и ùù0 º 0.

Следует также заметить, что 0 теперь включается в единицу 1, т.к. все включается в экран. Т.о. получаем, что 0É1. В то же время единица не включается в ноль, т.е. ù(1É0). Утверждение ùА теперь означает, что А есть ноль, следовательно, ùА есть единица. Поэтому утверждать какой-то смысл А в формальной логике есть то же, что предполагать его как логическую единицу, как экран Е. Истинами здесь как раз и считаются смыслы, которые в конечном итоге все могут быть представлены как логические единицы. Формальная логика по большому счету видит во всяком смысле только два состояния – либо логическую единицу, либо логический ноль. Она выступает как искусство различать эти состояния и определять, какое из них возникнет при той или иной комбинации единиц и нулей. В этом смысле формальную логику называют еще бинарной логикой, логикой абсолютного разделения истины и лжи.

Представленные выше первые три закона теперь могут быть записаны в терминах нуля и единицы в следующей форме:

1. Закон непротиворечия. 1× 0 º 0.

2. Закон полноты (исключенного третьего). 1 + 0 º 1.

3. Закон экстремальности (тождества). 1º 1.

Кроме отмеченных выше законов, могут понадобиться еще некоторые принципы, например, закон перестановочности умножения и сложения: Х×УºУ×Х, Х+УºУ+Х, и т.д., но мы о них уже не будем говорить специально. В целом возникает некоторая логическая алгебра смыслов, которая и получила название булевой алгебры в современной математической логике и математике (бинарная логика представляет из себя минимальную булеву алгебру на двух элементах 0 и 1).

Следует еще сказать несколько слов о Законе Тождества, который, с нашей точке зрения, неоднозначен и соединяет в себе множество различных принципов. В одной из наиболее глубоких своих формулировок этот закон утверждает, что истинное мышление может быть таковым только в том случае, если оно обладает абсолютной различимостью, т.е. не приравнивает неравное (нетождественное) и не начинает делать равное (тождественное) неравным. Хотя реально каждый человек может ошибиться, но все люди должны держать в сознании этот идеал и стремиться к нему. Только на этой основе возможно подлинное познание. В этом смысле Закон Тождества выступает как требование настройки сознания на некоторый идеал абсолютного разума, который никогда не ошибается, никогда ничего не забывает, не придумывает, но вечно пребывает как абсолютный свет истины. Этим светом все освещено и различено, причем освещено совершенно правильно. При такой формулировке Закон Тождества предполагает не просто экран сознания Е, но некоторый абсолютный экран Высшего Сознания Е_А, в рамках которого реализует себя наиболее точная и совершенная способность мышления. Хотя человек никогда в своей жизни не имеет дело с такой абсолютной способностью мышления и абсолютным экраном Е_А, но в нашем конечном сознании всегда есть некоторая система экранов Е₁, Е₂, …, Е_N, в которой есть высший экран Е_N, и в рамках этого экрана имитирует себя для человеческого разума абсолютный экран Е_А. Подобно тому как, начиная с некоторой высоты, более или менее высокие горы уже одинаково высоки для человека, стоящего у их подножия, так же и абсолютный экран Е_А перестает отличаться для человеческого разума от некоторого предельного для него в этот момент времени экрана Е_N. Существует как бы некоторый интервал тождества Т_N, - та система условий, в рамках которой экран Е_N перестает отличаться от абсолютного экрана Е_А, хотя все предшествующие экраны обнаруживают свое отличие. Это можно записать, например, в следующей форме:

(Е_N=E_A)¯T_N – N-й экран совпадает с абсолютным экраном в N-м интервале тождества T_N, и

(E_k<E_A)¯T_N – k-е экраны слабее («меньше») абсолютного экрана в N-м интервале тождества, где k<N. Слабость экрана сравнительно с идеалом абсолютного экрана проявляется для самого мыслителя в том, что человек сам для себя осознает, что рассуждает несовершенно, например, чувствует, что что-то забыл, что-то не учел, допустил ошибку, или принимает за ноль ненулевое, за абсолютное – относительное и условное. Однако, кроме самосознаваемой слабости, может быть и слабость с точки зрения тех идеалов мышления, которые вообще достигнуты на сегодня в культуре. В этом случае человек относительно общечеловеческого экрана сознания может мыслить слабо, но для него самого такой стиль мышления будет индивидуально совершенным.

Такая более глубокая формулировка Закона Тождества может тем не менее выражаться и в более формальных утверждениях вида ХºХ – «Х тождественно себе». Но это скорее символ правильной работы любого экрана сознания, его максимального уподобления абсолютному экрану. В совершенном экране равное должно оставаться равным (ХºХ), впрочем, как и неравное – неравным (ù(ХºùХ)), не должно возникать смешения, когда отождествляются неравные (ХºùХ) или раз-отождествляется равное (ù(ХºХ)).

Так в законах формальной логики являют себя некие первопринципы всякого правильного мышления.

§ 4. Формальные символические языки

На основе законов формальной логики может быть построен некоторый формальный символический язык, который лежит в основании всех логических теорий. В этом языке могут использоваться логические константы ноль (0) и единица (1), операции отрицания (ù), логического умножения (×), которое обычно называют конъюнкцией, логического сложения (+), называемого также дизъюнкцией, следования (импликации É) и равенства (º). Для кодирования смыслов используют также логические переменные. Их можно обозначать латинскими буквами p,q,r,s,t… Каждая такая буква обозначает нечто общее, что может быть в целом классе каких-то смыслов, например, суждений. Например, буквой р можно обозначить любое суждение, допустим, «Луна – спутник Земли», буквой q – суждение «Лев – травоядное животное». Первое суждение мы считаем правильным, что можно обозначить как равенство р единице, т.е. pº1, а второе суждение – ложным, что можно выразить как равенство q нулю: qº0. Тогда для сложных суждений мы также получим определенные значения истины или лжи (или, как говорят, истинностные значения). Например, из суждений «Луна – спутник Земли», «Лев – травоядное животное» можно образовать новое суждение «Луна – спутник Земли и Лев – травоядное животное», которое обозначается как умножение p×q (таким образом, логическое умножение обычно соответствует союзу «и» в естественном языке). Для такого сложного суждения мы получим: p×q º 1× 0 º 0, т.е. оно окажется ложным. Далее из тех же простых суждений р и q, можно образовать суждение-сумму «Луна – спутник Земли или Лев – травоядное животное», т.е. p+q (логическое сложение обычно соответствует союзу «или» в естественном языке). Для него получим: p+q º 1+0 º 1. Следовательно, это суждение будет истинным.

Простейший вариант дедуктивной логики, который носит название исчисление высказываний (суждений), примерно так и строится. Здесь вводятся логические переменные и константы, операции, и из простых суждений на основе операций строятся более сложные суждения. Зная истинностные значения простых суждений, можно определять истинностные значения сложных суждений. Возникает некоторый формальный символический язык – язык исчисления высказываний. В силу его простоты, мы можем его описать очень точно.

Для описания искусственных языков, вначале описывают их алфавит, т.е. множество букв этого языка, из которых строятся слова, или выражения данного языка. Затем указывают правила построений таких выражений. Искусственные языки тем и отличаются от естественных разговорных языков, что у первых есть обычно довольно простые правила построения всех своих выражений. Например, язык исчисления высказываний может использовать такой алфавит:

Константы: 1, 0

Переменные: p,q,r,s,t…

Операции: ù, ×, +, É, º

Скобки: (, )

Выражения языка исчисления высказываний называют еще формулами. Все формулы могут быть построены индуктивно по следующим правилам:

(1) Базис индукции: любая константа или переменная есть формула.

(2) Индуктивное предположение: если А, В – уже построенные формулы, то ù(А), ((А)×(В)), ((А)+(В)), ((А)É(В)) и ((А)º(В)) – также формулы.

(3) Индуктивное замыкание: никаких иных формул нет.

Таким образом, в базисе индукции здесь определяются некоторые стартовые формулы, с которых начинается построение множества всех формул, а в индуктивном предположении указываются некоторые правила порождения (отрицание, умножение, сложение, следование и равенство) из уже построенных формул новых формул. Так, многократно обращаясь на множество сначала стартовых, а затем все новых формул, будет прирастать до бесконечности множество формул языка исчисления высказываний. Здесь мы имеем дело с использованием схемы математической индукции по отношению к формулам, а не числам. Условие (3) индуктивного замыкания требует, чтобы среди формул были только такие выражения, которые можно вывести из первых двух пунктов. В противном случае, если бы пункта (3) не существовало, то мы бы лишь утверждали, что любое выражение, вытекающее из пунктов (1) и (2), есть формула, но не наоборот, т.е. могло бы оказаться и так, что не всякая формула была бы выражением, построенным по правилам (1) и (2), что само по себе не противоречит этим пунктам.

Пусть, например, у нас в алфавите всего две переменных p и q, и нет констант. Тогда стартовыми формулами будут всего две формулы: p, q. Затем, согласно индуктивному предположению, мы можем образовать следующие новые формулы: ù(p),ù(q), ((p)×(p)), ((q)×(q)), ((p)×(q)), ((q)×(p)), ((p)+(p)), ((q)+(q)), ((p)+(q)), ((q)+(p)), ((p)É(p)), ((q)É(q)), ((p)É(q)), ((q)É(p)), ((p)º(p)), ((q)º(q)), ((p)º(q)), ((q)º(p)). Теперь мы можем прибавить эти формулы к формулам p и q, и вновь применить уже к этому расширенному множеству все возможные логические операции во всех возможных комбинациях. Здесь, например, появятся формулы вида ((ù(p))É(q)), (((p)É(q))+((q)º(q))), и т.д. Поскольку количество всех скобок начинает в этом случае резко возрастать, то обычно договариваются о сокращении ряда скобок. Например, пишут ùр вместо ù(р), или pÉq вместо ((p)É(q)).

В формальном языке обычно можно проверить только по внешней форме, является ли та или иная последовательность букв алфавита этого языка его определенным выражением, или нет. Например, чтобы проверить, является ли формулой языка исчисления высказываний последовательность букв ù(pÉ(q+r)) (с учетом сокращений скобок), мы должны начать проверку с самых элементарных формул, входящих в это выражение, постепенно поднимаясь все выше, пока не дойдем до всего выражения в целом. Здесь:

1. Переменные p, q, r являются формулами по базису индукции.

2. Если q, r – формулы, то, согласно индуктивному предположению, и (q+r) – тоже формула.

3. Если p и (q+r) – формулы, то, согласно индуктивному предположению, и (pÉ(q+r)) – тоже формула.

4. Наконец, если (pÉ(q+r)) – формула, то, согласно индуктивному предположению, и ù(pÉ(q+r)) – тоже формула.

Так мы доказываем, что выражение ù(pÉ(q+r)) есть формула языка исчисления высказываний.

Подобная проверка не сможет подтвердить, например, что выражение pp является формулой языка исчисления высказываний, т.к., хотя р – это формула, но из формул р и р мы никакими способами, указанными в индуктивном предположении, не сможем получить выражения рр.

В общем случае любые последовательности букв алфавита называются выражениями языка, а некоторые специальные последовательности, выстраиваемые на основе индуктивных правил, - правильно построенными выражениями языка. Формулы – пример правильно построенных выражений (правильно построенных формул) в языке исчисления высказываний.

Построение формального языка не заканчивается на этапе построения его формул или других специальных выражений языка. Обычно ко второму этапу построения формального языка относят также построение его логики как чисто формальной структуры.

Для построения формальной логики, среди всех формул языка выделяют некоторое множество формул, которые называют аксиомами языка. Выделяют также некоторые правила логического вывода, которые позволяют от одного множества формул (посылок) переходить к другому множеству формул (заключениям). Например, в языке исчисления высказываний в качестве аксиом могут приниматься формулы, выражающие законы непротиворечия, исключенного третьего, тождества и т.д. В качестве правила логического вывода во многих дедуктивных теориях используется так называемое правило отделения, или modus ponens, которое выглядит следующим образом:

p, pÉq

q

Как и ранее, правило вывода здесь изображено в виде дроби, где над чертой написаны посылки, под чертой – заключение. Правило отделения позволяет от формул p и (pÉq) перейти к формуле q. Это правило удовлетворяет условию переноса истинности: если pº1 и, (pÉq)º1, то qº1.

Применяя правила вывода к аксиомам, мы можем получить некоторые формулы, которые называют теоремами формального языка. Затем, применяя правила вывода к аксиомам и уже полученным теоремам, мы можем получать новые теоремы. Здесь также можно использовать индуктивное определение множества всех теорем формального языка, что существенно облегчает работу с логической структурой этого языка.

Язык исчисления высказываний – один из самых простых формальных языков. Но именно этот язык так или иначе лежит в основании всех более сложных формальных дедуктивных систем. Языки этих систем обычно получаются на основе того или иного обогащения языка исчисления высказываний новыми логическими средствами. Например, одно из наиболее распространенных обогащений такого рода – использование так называемых кванторов.

Во многих суждениях используется логическая структура вида «Для любого х верно, что Р(х)», где Р – некоторое свойство. Например, в такой форме могут быть записаны заключения в различных индуктивных выводах (см. выше). Отрицанием суждения «Для любого х верно, что Р(х)» является суждение «Существует такой х, что ùР(х)» - именно в такой форме могут быть записаны контрпримеры для индуктивного заключения. Оборотам «Для любого х верно, что …» и «Существует такой х, что …» сопоставляют специальные логические структуры – квантор всеобщности "х (символ " взят от англ. «Аll» - все) и квантор существования $х (от англ. «Exist» - существовать) соответственно. В этом случае суждение вида «Для любого х верно, что Р(х)» записывается как "хР(х), а суждение «Существует такой х, что Р(х)» - как $хР(х). Обогащение языка исчисления высказываний переменными для объектов (типа x, y, z, …), переменными для предикатов (типа P, Q, R,…) и кванторами по объектным переменным (типа "х, $х) приводит к построению более сложного и мощного формального языка, который называется языком исчисления предикатов первого порядка (поскольку предикаты и кванторы здесь берутся по объектным переменным, которые еще называют переменными первого порядка). Формулы с кванторами определяются таким образом, что "хР(х) º 1 равносильно тому, что Р(а₁) º 1 и Р(а₂) º 1 и Р(а₃) º 1 и т.д., где а₁, а₂, а₃, … - все частные значения объектной переменной х. Истинность формулы $хР(х), т.е. верность равенства $хР(х) º 1, равносильна тому, что Р(а₁) º 1 или Р(а₂) º 1 или Р(а₃) º 1 и т.д., т.е. используется логическое сложение (союз «или») вместо логического умножения (союза «и»). В этом смысле кванторные формулы предполагают бесконечные конъюнкции и дизъюнкции формул языка исчисления высказываний, так что переход от исчисления высказываний к исчислению предикатов – это некоторая разновидность перехода от конечного к бесконечному в логике.

§ 5. Синтаксис и семантика

При построении формальных символических языков, используемых в разного рода дедуктивных системах, обычно достаточно строго определяют и различают синтаксис и семантику языка. Как мы уже отмечали выше, синтаксис формального языка есть система правил построения различных выражений этого языка – букв алфавита, правильно построенных формул и т.д. - и чисто формальных операций с ними. Именно к синтаксису языка относятся разного рода индуктивные правила построения формул, теорем и других выражений языка. Синтаксис выражает момент формы в языке, получающий свое представление в системе знаков этого языка, в правилах преобразования знаков, не требующих, как это обычно считают, понимания смысла этих знаков. Например, синтаксическими правилами преобразования формул в языке исчисления высказываний является вывод теорем из аксиом в согласии с правилами вывода. Конечно, по-видимому, трудно найти такое преобразование выражений языка, в котором совершенно отсутствовала бы опора на некоторый смысл и содержание. Например, те же правила логического вывода вначале были выведены тем или иным мыслителем из интуиции и других содержательных оснований. Но после того как они были закреплены в форме некоторого искусственного языка, можно было изменить позицию по отношению к этим правилам и рассмотреть их чисто формально – как некоторые фиксированные преобразования знаков, независимо от наполняющего эти знаки смысла. И такой момент независимости логической формы может существовать, как мы уже отмечали, в каждом искусственном языке. Этот момент и доводится до предела, до чистоты в идее синтаксиса языка.

Наверное каждый из нас, решая в школе задачки по математике, замечал, что, проводя преобразования над формулами, можно на время забыть, что именно обозначают эти формулы, и преобразовывать их чисто формально – в согласии с некоторыми правилами вычисления. Например, в решении задачи мы могли столкнуться с формулой t = х(y-z)+xz и раскрыть здесь скобки, переходя к равносильной формуле t = xy-xz+xz, а затем отбросить последние два слагаемых, получив в итоге величину t = xy. Если аккуратно записать эти преобразования, то мы получим такую последовательность формул:

t = х(y-z)+xz

t = xy-xz+xz

t = xy+0

t = xy

При решении таких задач можно отвлечься и забыть, что именно обозначают t, x, y и z, воспринимая их в момент вычислений как некоторые формальные символы, способные обозначать любые числа. Тогда и преобразования с такими значками также приобретут формальный характер, принимающий во внимание лишь форму знаков и правила преобразования этой формы. Вот это и есть момент синтаксиса, чистой формы, в жизни формального языка.

Однако ни один, даже самый формализованный язык, не может обойтись совершенно без обращения к смыслу и содержанию используемых в нем знаков. Более того, как отмечалось выше, именно те искусственные языки, которые обычно называют формальными, - это как правило примеры языков, которые изначально строились таким образом, чтобы их форма обладала максимальным подобием некоторому содержанию. Это может показаться парадоксальным, но только благодаря этому повышенному подобию содержанию, языковая форма впоследствии приобрела возможность самостоятельного существования. Семантика – это система правил, позволяющих наделить определенные выражения языка смыслом и значением. О семантике языка обычно говорят в том случае, когда так или иначе важным моментом становится не только форма языка, но и то, что она обозначает – ее содержание.

Со времени работы немецкого математика Готлоба Фреге «Значение и смысл» стало общепринятым выделение двух видов содержания всякого знака – смысла (коннотата) и значения (денотата). Обычно знак, например, слово «Луна» обозначает некоторый предмет, в данном случае – планету Луну. Такой предмет называют денотатом знака. Но, кроме того, слово «Луна» обладает и некоторым смыслом, который может быть выражен, например, в определении Луны как спутника Земли. Такое смысловое содержание знака называют коннотатом. Придание содержания знаку означает в этом случае связывание со знаком как некоторым языковым объектом его денотата или коннотата. Если для задания содержания знака в языке предполагается достаточным задание только денотатов, то в этом случае говорят об экстенсиональной (или одноуровневой) семантике языка, поскольку денотат еще называют экстенсионалом знака. Если же содержание знака предполагает определение и денотата и коннотата, то говорят об интенсиональной (двухуровневой) семантике языка (т.к. коннотат также называют интенсионалом знака). Экстенсиональные семантики проще, т.е. легче выразить предмет, обозначаемый знаком, чем смысл знака. Например, язык исчисления высказываний или исчисления предикатов предполагает задание как раз экстенсиональной семантики. Заслуга строгого определения семантики для экстенсиональных языков принадлежит польскому логику Альфреду Тарскому, который во многом опирался в решении этой проблемы на идеи своего учителя Станислава Лесьневского. Согласно Тарскому, семантика формального языка есть система правил, которая позволяет каждому выражению из некоторого специального класса всех выражений языка сопоставить его денотат, т.е. некоторый предмет, обозначаемый этим знаком. Как правило, денотатами выражений в формальных языках науки являются различные составляющие тех или иных математических структур, например, числа, вектора, функции и т.д. Более того, формальные языки обычно и создаются с целью описания свойств тех или иных математических структур, например, структур на числах, на векторах, на функциях, на множествах, и т.д. В этом случае необходимо различать саму структуру и тот формальный язык, который ее описывает (по отношению к такому языку математическая структура называется также моделью этого языка). Когда форма искусственного языка создана и, отрываясь от первоначального содержания, получает момент самостоятельности, содержание языка оказывается внешним по отношению к самому языку, начинает отличаться учеными от языка как чисто знаковой системы. Такая установка по отношению к языкам науки получила преобладающее развитие в 20-м веке. Несомненно, момент внешности языковой формы и содержания имеет место, но, по-видимому, не стоит его абсолютизировать. Как мы увидим позднее, именно гипертрофия формального момента в понимании научного познания и его языковых средств привела ко многим проблемам и кризисным явлениям философии науки в последнее время.

Возвращаясь к примеру с математическими вычислениями, мы можем вновь рассмотреть фрагмент вычислений, позволяющий перейти от выражения х(y-z)+xz к выражению xу. Обычно, в каждой задаче есть какие-то начальные условия, например в форме равенств x = 2 и у = 7. Мы можем подставить на место переменных x и у их частные значения x = 2 и у = 7, данные в начальных условиях, и получить частное значение для выражения xу. Таким образом, получим 2×7 = 14. В такого рода преобразованиях мы уже приближаемся к заданию содержания знаков. Мы переходим от переменных x и z к их частным значениям 2 и 7. Такая логическая операция носит название подстановки – на место переменных подставляются их частные значения. В результате подстановки у нас получается более конкретное выражение, не содержащее переменных. Именно такие конкретные выражения могут получить свои денотаты. В нашем случае денотатом знака 14 будет число четырнадцать. Здесь следует понимать, что выражение «14» - это не само число, но только его знак в математическом языке. Например, в римской записи оно будет обозначаться через знак XIV, в семиричной системе счисления – через знак 100, и т.д. Что же касается числа четырнадцать, то это некоторый идеальный объект, который невозможно увидеть глазами, но можно только мыслить. Это элемент математической структуры на числах. Так вот, при задании семантики мы связываем знак 14 с идеальным объектом – числом четырнадцать. Только такая связь позволяет нам, оперируя со знаком «14», иметь в виду нечто гораздо большее – идеальную сущность, живущую в нашем сознании и в какой-то форме принадлежащую реальному миру.

Здесь нужно отметить одну интересную особенность построения теории семантики всякой языковой системы. В чистом виде, для выражения семантики, нам нужно было бы вообще выйти за пределы языка, обращаясь к самим денотатам – предметам, числам и т.д. Однако для выражения семантики как теории нам также необходим некоторый язык, в рамках которого мы могли бы выражать как знаки, так и их содержания. В таком «семантическом языке» содержаниями знаков могут становиться сами знаки, а знаки денотатов должны будут заменять собою денотаты для исследуемого языка. Так появляются «более семантические» знаки, через которые в семантике обозначают денотаты некоторой языковой системы L, причем, для самой этой системы знаки денотатов представляют сами денотаты. Говоря об одном языке L, мы не можем не использовать другого языка L*. Язык L*, благодаря которому мы говорим о семантике или синтаксисе языка L, называют в этом случае метаязыком по отношению к L, а язык L – объектным языком по отношению к L*. Так решается парадокс теории языка – мы выходим не вообще за пределы языка, но лишь за пределы объектного языка, оставаясь в рамках метаязыка. Например, говоря о числе четырнадцать как денотате знака «14», мы ведь тоже использовали некоторый знак «число четырнадцать» в рамках русского языка, который играл роль метаязыка в этом случае. Поэтому определение содержания знака «14» может быть символизировано в виде связи двух знаков – знака «14» из объектного языка математики и знака «число четырнадцать» из русского языка. При построении теории семантики как формального языка, для представления денотатов могут использоваться даже те же знаки, что и в объектном языке, но с некоторым дополнительным индексом, указывающим на принадлежность знака семантическому метаязыку.