КОНЦЕНТРИЧЕСКИЕ ЗАРЯЖЕННЫЕ СФЕРЫ

Читатель:Внутри сплошного проводника есть полость произвольной формы (рис. 12.1). Проводнику сообщили некоторый заряд Q. Как распределится заряд по проводнику?

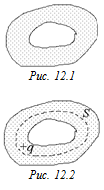Автор: Как мы уже знаем, внутри проводника заряд находиться не может. Значит, остаются две возможности: заряд распределится по внутренней поверхности полости или по внешней поверхности проводника.

Предположим, что некоторый заряд q находится на внутренней поверхности проводника. Рассмотрим мысленно замкнутую поверхность S, внутри которой окажется заряд q (рис. 12.2). Тогда поток вектора напряженности через эту поверхность будет равен

.

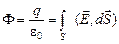Но поскольку 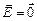в любой точке нашей поверхности, то Ф = 0, а тогда и q = 0. Значит, на внутренней поверхности полости заряда нет, и остается единственная возможность: весь заряд находится на наружной поверхности проводника.

Автор: Как Вы думаете, возможно ли существование электрического поля внутри полости проводника, заряженного зарядом Q?

Читатель: Раз мы доказали, что заряда на внутренней поверхности полости нет, то и никакого поля внутри полости быть не может.

Автор: Не обязательно. Например, две плоские пластины с зарядами +q и –q в сумме имеют нулевой заряд, но между ними существует электрическое поле (рис. 12.3). Поэтому если на внутренней поверхности полости есть положительные и отрицательные заряды (пусть при этом q⁺ + q^– = 0!), то электрическое поле внутри полости вполне может существовать.

Читатель: Действительно.

Автор: И все же поля внутри полости нет. Но докажем это строго.

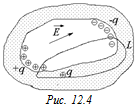Предположим, что на поверхности полости есть заряды +q и –q и между ними существует электрическое поле (рис. 12.4). Возьмем замкнутую линию L, такую, что внутри полости эта линия совпадает с силовой линией электрического поля, а остальная часть линии проходит через проводник.

Мысленно переместим заряд +q вдоль этой линии по замкнутому контуру. Тогда работа поля на участке внутри полости будет явно положительная, так как сила там будет в любом месте сонаправлена с перемещением (мы выбрали именно такую траекторию движения заряда). А на том участке, где линия проходит через проводник, работа равна нулю, так как внутри проводника .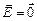

Таким образом, общая работа по перемещению заряда вдоль нашего замкнутого контура, совершенная силами электростатического поля, положительна! Но мы знаем, что на самом деле эта работа должна равняться нулю: иначе у нас получился бы вечный двигатель. Мы пришли к противоречию, значит, внутри полости поля нет!

Заметим, что из наших рассуждений следует важный практический вывод: внутри металлического ящика электрического поля быть не может, а значит, в металлическом ящике можно спрятаться от сильных внешних полей!

СТОП! Решите самостоятельно: А4–А7, В13.

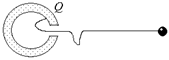Рис. 12.5

Автор: Как Вы думаете, зарядится ли незаряженный металлический шар, если его соединить с внутренней поверхностью заряженной сферы (рис. 12.5)?

Читатель: Так как заряд на внутренней поверхности сферы отсутствует, то шар зарядиться не может.

Автор: Не будем торопиться с выводами. Будем считать, что незаряженный шар находится от заряженной сферы достаточно далеко. Чему равен его потенциал?

Читатель: 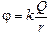. Если r ® ¥, то j = 0.

Автор: А чему равен потенциал внутри сферы?

Читатель: Потенциалу на поверхности: , где R – радиус сферы, а Q – ее заряд.

Автор: Значит, если Q > 0, то j_сферы > j_шара? Не так ли? А мы знаем, что положительный заряд всегда перетекает из точки с бóльшим потенциалом в точку с меньшим потенциалом! Следовательно…

Читатель: Вы хотите сказать, что шар зарядится? Но откуда же возьмутся заряды, если на внутренней поверхности сферы их нет?!

Автор: Зато на шаре сколько угодно электронов! Положительно заряженная сфера притянет часть этих электронов к себе и «высадит» их на внутреннюю поверхность, уменьшив тем самым

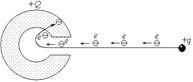Рис. 12.6

положительный заряд сферы (рис. 12.6). А на шаре при этом из-за недостатка электронов создадутся положительные заряды! СТОП! Решите самостоятельно: А1, А2.

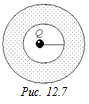Автор: Как Вы думаете, что произойдет, если заряженный шар, находящийся внутри сферы, соединить с внутренней поверхностью сферы (рис. 12.7)?

Читатель: Мы уже выяснили, что на внутренней поверхности полости проводника никаких зарядов быть не может. Наш шар вместе с проволочкой, соединяющей его со сферой, представляет собой как бы часть внутренней поверхности полости сферы. А значит, заряд с шарика должен целиком перейти на наружную поверхность сферы, независимо от того, заряжена она или нет!

СТОП! Решите самостоятельно: А9.

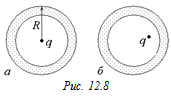Задача 12.1. Внутри незаряженной металлической сферы с внешним радиусом R находится точечный заряд q. Как распределится индуцированный заряд по внешней и внутренней поверхности сферы? Рассмотреть случаи, когда: а) заряд находится в центре сферы (рис. 12.8,а); б) заряд смещен от центра (рис. 12.8,б).

Решение.

Случай а. Прежде всего заметим, что сейчас на внутренней поверхности сферы должен появиться заряд, индуцированный (наведенный) точечным зарядом q, так как заряд q притягивает к себе заряды противоположного знака, а по металлу заряды могут перемещаться свободно.

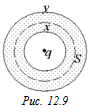Обозначим величину заряда на внутренней поверхности сферы х, а на внешней – у. Рассмотрим поверхность S, целиком лежащую в металле (рис. 12.9). Согласно теореме Гаусса поток через эту поверхность будет равен

,

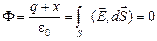так как 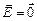в металле. Тогда 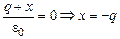. Поскольку в целом сфера не заряжена, то

х + у = 0 Þ у = –х = –(–q) = +q.

Итак, x = –q; у = +q. Ясно, что из соображения симметрии и по внешней, и по внутренней поверхностям заряд распределен равномерно.

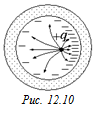Случай б. Если заряд будет смещен от центра, то величина индуцированных зарядов х и у от этого не изменится. Но очевидно, что чем ближе заряд q будет к внутренней поверхности сферы, тем сильнее он будет притягивать к себе свободные заряды, а значит, тем выше будет их поверхностная плотность. То есть заряд на внутренней поверхности сферы будет распределен неравномерно (рис. 12.10).

Читатель: Наверное, примерно такая же картина будет и на наружной поверхности сферы (рис. 12.11)?

Автор: А вот и нет! На наружной поверхности распределение зарядов будет по-прежнему равномерным (рис. 12.12).

Читатель: Честно говоря, не понятно.

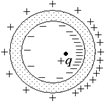Рис. 12.11 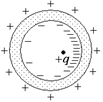Рис. 12.12

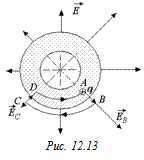Автор: А давайте предположим, что распределение зарядов на наружной поверхности действительно неравномерное, как на рис. 12.11. Тогда ясно, что поле, созданное этими зарядами, будет больше там, где больше плотность зарядов, и меньше там, где эта плотность меньше (рис. 12.13).

Возьмем контур ABCD и мысленно переместим по нему заряд +q. На участке АВ работа поля будет положительной, а на участке CD – отрицательной, причем так как Е_В >Е_С, то |A_AB| > |A_CD|.

На участках ВС и BD работа, очевидно, равна 0. Значит, общая работа на всем пути положительна! А этого быть не может. Следовательно, наше предположение о том, что заряд на наружной поверхности распределен неравномерно, ошибочно. То есть правильная картина распределения заряда показана на рис. 12.12.

СТОП! Решите самостоятельно: А8, В21, С5, С7, С15.

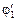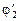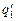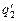Задача 12.2. Два заряженных шара соединили длинным тонким проводником (рис. 12.14). Первый шар имеет заряд q и радиус r, второй – заряд Q и радиус R. Найти: 1) потенциалы шаров j₁ и j₂ до соединения и и после соединения; 2) заряды шаров и после соединения; 3) поверхностные плотности зарядов σ₁ и σ₂ до соединения 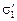и и 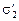после соединения; 4) энергию системы W до соединения и W¢ после соединения; 5) количество выделившейся теплоты Q_т.

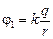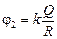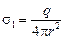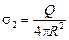Q, R, q, r	Рис. 12.14 Решение. До соединения: 1) ; ; 2) ; (площадь поверхности шара радиуса rS = 4πr2); 3) W = W1 + W2 = 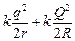(энергия сферы радиуса r и заряда q равна ).
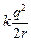j1, j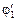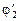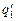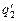2 = ? , = ? , = ? σ1, σ2, = ? 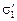, 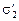= ? W, W¢ = ? Qт = ?

После соединения потенциалы шаров стали равны, так как поверхность единого проводника всегда эквипотенциальная:

= = .

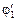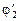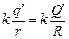Общая сумма зарядов при этом не изменилась: q + Q = q¢ + Q¢. Мы получили систему с двумя неизвестными q¢ и Q¢:

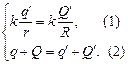
Выразим из (1) Q¢:

; .

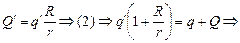
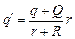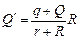Тогда

.

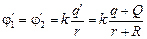СТОП! Решите самостоятельно: В1, В2, В5, В7.

Вычислим поверхностные плотности зарядов после соединения:

;

.

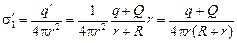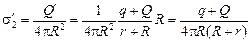Заметим, что если r ® 0, то 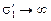, т.е. при уменьшении размеров маленького шарика плотность зарядов на нем будет неограниченно возрастать. Вот почему наибольшая плотность зарядов наблюдается на остриях металлических предметов.

СТОП! Решите самостоятельно: В9, В15.

Энергия шаров после соединения равна

.

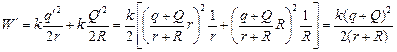Количество выделившегося тепла равно убыли энергии электрического поля:

.

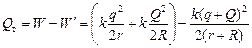Проведя несложные алгебраические преобразования, нетрудно получить

.

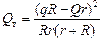Читатель:Из этой формулы следует, что если qR ¹ Qr, то Q_т > 0, если же qR = Qr, то Q_т = 0. Почему?

Автор: Да потому, что если qR = Qr, то 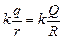, т.е. потенциалы шаров 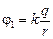и 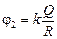до соединения равны. А это значит, что после соединения шаров никакого перемещения зарядов не будет.

СТОП! Решите самостоятельно: В23, С3.

Задача 12.3. Даны две концентрические металлические сферы радиусами R₁ и R₂ и зарядами q₁ и q₂ соответственно. Определить потенциалы: а) в центре сфер; б) на поверхности второй сферы; в) на расстоянии r > R₂ от центра.

R1, R2 q1, q2 r > R2	Решение. Построим график зависимости j(r) для каждой из сфер по отдельности (рис. 12.15).   Рис. 12.15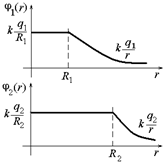
j(0) = ? j(r) = ? j(R2) = ?

Потенциал общего поля этих сфер является алгебраической суммой потенциалов каждого из полей, созданных сферами:

j = j₁ + j₂.

Построим график j(r) как сумму графиков j₁(r) и j₂(r) (рис. 12.16). Из графика легко получаем ответ:

; ; .

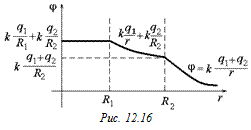
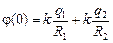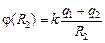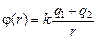СТОП! Решите самостоятельно: В19, С10–С12.

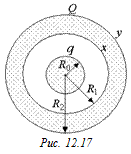Задача 12.4. В центре проводящего сферического слоя с внутренним радиусом R₁ и внешним радиусом R₂ находится металлический шар радиуса R₀ и с зарядом q. Сферический слой имеет заряд Q (рис. 12.17). Построить графики E(r) и j(r), нарисовать картину силовых линий и найти индуцированные заряды х и у на внутренней и внешней поверхностях сферического слоя.

Рассмотрим участок [R₀; R₁]. Возьмем сферу радиусом r (R₀ < r < R₁) и запишем поток вектора 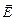через сферу:

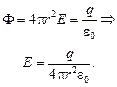
Как видим, это поле ничем не отличается от поля точечного заряда q, расположенного в центре шара.

Рассмотрим участок [R₂; ¥). Возьмем сферу радиусом r > R₂ и запишем закон Гаусса:

.

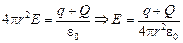Как видим, это поле точно такое же, как поле точечного заряда величиной (q + Q), расположенного в центре шара.

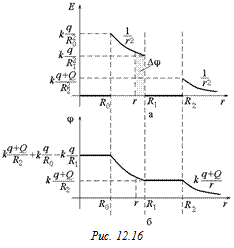
2. Строим график j(r) (рис. 12.18,б).

На участке [R₂; ¥) потенциал такой же, как потенциал поля точечного заряда (q + Q):

.

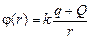На участке [R₁; R₂] 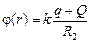= const, так как Е = 0.

Наиболее трудный участок графика [R₀; R₁]. Потенциал в точке r Î [R₀; R₁] равен сумме величин 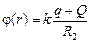и Dj – площади под графиком Е(r) на участке [r; R₁] (рис. 12.18,а); 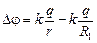. Тогда .

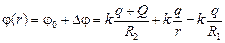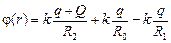На участке [0; R₀] = const, так как Е = 0.

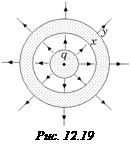
3. Рисуем картину силовых линий (рис. 12.19). Найдем индуцированные заряды х и у. Поскольку поток через сферу радиусом r (R₀ < r < R₁) равен нулю, то

.

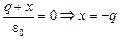А поскольку общий заряд сферического слоя равен Q, то

х + у = Q Þ –q + y = Q Þ y = q + Q.

СТОП! Решите самостоятельно: В21, С13, С17.