СПЛОШНЫЕ ПРОВОДНИКИ
В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ
Проводники
Проводником называется такое вещество, в котором носители электрического заряда – электроны – могут свободно перемещаться по объему тела под действием электрического поля.
Напряженность электростатического поля внутри проводника всегда равна нулю, если по проводнику не течет ток.
В самом деле: если 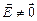 , то на каждый электрон начинает действовать сила
, то на каждый электрон начинает действовать сила 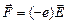 , и в проводнике происходит перераспределение заряда (т.е. ток), которое продолжается до тех пор, пока поле в проводнике не станет равным нулю.
, и в проводнике происходит перераспределение заряда (т.е. ток), которое продолжается до тех пор, пока поле в проводнике не станет равным нулю.
Задача 11.1. Сплошной металлический шар радиуса R имеет заряд Q. Построить графики зависимости напряженности и потенциала от расстояния до центра шара.
| R, Q | Решение. Пусть 0 < r < R. Так как по проводнику не течет ток, то Е = 0. | ||
| Е(r) = ? j(r) = ? | |||
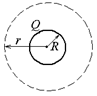 Рис. 11.1
Рис. 11.1
| Пусть r ³ R. Применим теорему Гаусса (рис. 11.1). Поток вектора 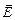 через сферу радиусом r равен через сферу радиусом r равен
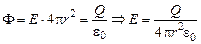 .
График E(r) (рис. 11.2,а) ничем не отличается от аналогичного графика для поля равномерно заряженной сферы. .
График E(r) (рис. 11.2,а) ничем не отличается от аналогичного графика для поля равномерно заряженной сферы.
| ||
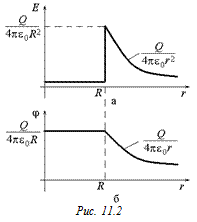 Ясно, что по этой же причине и график j(r) должен быть точно таким же, как и в случае поля равномерно заряженной сферы (рис. 11.2,б).
Ясно, что по этой же причине и график j(r) должен быть точно таким же, как и в случае поля равномерно заряженной сферы (рис. 11.2,б).
СТОП! Решите самостоятельно: А2, А5, А6, А8, В6.
Между любыми двумя точками внутри проводника любой формы разность потенциалов равна нулю, если по проводнику не течет ток.
В самом деле, возьмем внутри произвольного проводника две произвольные точки 1 и 2 (рис. 11.3) и проведем через них ось х.
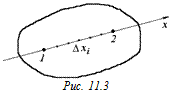 Разобьем отрезок [x1; x2] на малые отрезки Dхi:
Разобьем отрезок [x1; x2] на малые отрезки Dхi:
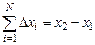 .
.
Тогда разность потенциалов
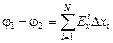 .
.
Поскольку 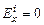 в любой точке проводника, то j1 – j2 = 0, что и требовалось доказать.
в любой точке проводника, то j1 – j2 = 0, что и требовалось доказать.
Таким образом, потенциал любой точки любого проводника везде одинаковая величина:
j = const. (11.1)
Заметим, что при этом не имеет значения, заряжен проводник или не заряжен, находится он во внешнем поле или нет!
СТОП! Решите самостоятельно: А1, А3.
Читатель: В 8 классе мы обсуждали вопрос о том, как распределен заряд по заряженному проводнику. Насколько я помню, утверждалось, что заряд распределяется только на поверхности проводника. А нельзя ли доказать, что это именно так и есть?
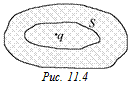 Автор: Конечно, можно! Давайте предположим, что внутри сплошного проводника находится некоторый заряд q. Мысленно окружим его произвольной поверхностью S, целиком лежащей внутри проводника (рис. 11.4). Тогда по теореме Гаусса поток через эту поверхность
Автор: Конечно, можно! Давайте предположим, что внутри сплошного проводника находится некоторый заряд q. Мысленно окружим его произвольной поверхностью S, целиком лежащей внутри проводника (рис. 11.4). Тогда по теореме Гаусса поток через эту поверхность

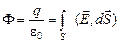 .
.
Так как 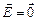 в любой точке поверхности S, то Ф = 0, а значит, и q = 0, что и требовалось доказать.
в любой точке поверхности S, то Ф = 0, а значит, и q = 0, что и требовалось доказать.
Итак, запомним: внутри сплошного проводника заряд находиться не может! Весь заряд находится только на поверхности проводника!
Задача 11.2. Три заряженных капельки ртути радиуса r = 1,0 мм и с зарядом q = 1,0×10–9 Кл каждая слились в одну каплю. Определить потенциал большой капли.
| п = 3 r = 1,0 мм q = 1,0×10–9 Кл | Решение. При слиянии капель сохраняются две величины: общий объем капель и общий заряд. Отсюда можно записать два уравнения:
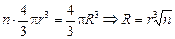 ; nq = Q. ; nq = Q.
|
| j = ? | |
Потенциал большой капли  , подставим в эту формулу значения R и Q:
, подставим в эту формулу значения R и Q:
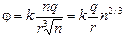 =
= 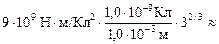
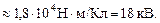
Ответ: 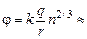 18 кВ.
18 кВ.
СТОП! Решите самостоятельно: В9, С3, С4, D1.
Дата добавления: 2016-04-11; просмотров: 1108;
