Действие магнитного поля на проводники с током и движущиеся заряды

Из ориентирующего действия магнитного поля на рамку с током следует, что на стороны рамки (проводники с током) действует сила со стороны магнитного поля. Ампером было установлено, что эти силы определяются следующим соотношением (законом Ампера):

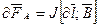(7.4)

или соответственно

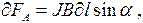(7.5)

где - сила, действующая со стороны магнитного поля на элемент проводника 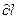, по которому течет ток J ; 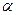- угол между векторам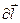и и .

Из (7.4) следует, что вектор 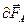направлен как векторное произведение векторов 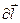и , откуда и формируется вспомогательное правило левой руки: если ладонь левой руки расположить так, что бы в неё входил вектор , а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы Ампера. Закон Ампера позволяет выяснить физический смысл модуля вектора магнитной индукции: «основной силовой характеристики магнитного поля». Из (7.5) следует, что

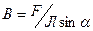. (7.6)

При J = 1 А, l = l м, sin α = 1 из (7.6) вытекает, что B = F_A , то есть модуль вектора магнитной индукции равен силе Ампера, действующей на проводник с током единичной длины, по которому течет единичный ток и который перпендикулярен направлению поля. В «СИ» единица магнитной индукции - 1 Тесла [Тл = Н/(А·м)].

Из закона Ампера следует, что воздействие одного тока на другой должно носить характер взаимодействия (рис. 7.2). Каждый из двух бесконечных прямолинейных токов J₁ и J₂ (расстояние между которыми R) создают магнитное поле, которое действует на другой проводник с током.

Рис. 7.2

Ток J₁ создает магнитное поле, направление которого 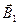задается правилом правого винта (см. рис. 7.2), а его модуль, согласно (7.3) равен 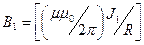. Направление силы 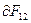, с которой поле 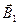действует на участок 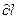второго тока, определяется по правилу левой руки (см. рис. 7.2). Модуль 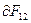в соответствии с (7.3) равен 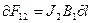и далее

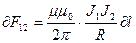. (7.7)

Рассуждая аналогично можно показать, что сила 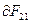, с которой магнитное поле действует на элемент 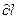первого проводника с током 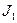направлена в противоположную сторону и равна по модулю

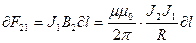, (7.8)

то есть два параллельных тока одинакового направления притягиваются друг к другу силой

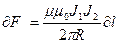. (7.9)

Соответственно между токами противоположного направления действует сила отталкивания, определяемая выражением (7.9).

Так как магнитное поле действует на проводники с током, в которых движутся заряды, то оно должно действовать и на один электрический заряд Q , движущийся в магнитном поле со скоростью 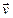. Такая сила получила название сила Лоренца и выражается формуло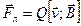й или

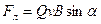, (7.10)

где 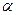- угол между векторам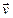и и . Направление силы Лоренца определяется с помощью модифицированного правила левой руки: если ладонь левой руки расположить так, что бы в нее входил вектор , а четыре вытянутых пальца направить вдоль вектора 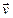для Q > 0 (и против вектора 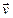для Q < 0), то отогнутый большой палец покажет направление силы Лоренца.

Согласно (7.10) 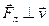, то есть сила Лоренца работы не совершает, и кинетическая энергия заряженной частицы не меняется. Таким образом, при движении заряженной частицы в магнитном поле её скорость не меняется по величине, а меняется только по направлению. Соотношение (7.10) позволяет проанализировать возможные варианты движения заряженных частиц в однородном магнитном поле. Рассмотрим простейшие частные случаи и общий случай этого движения.

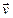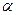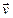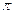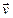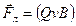Если заряженная частица движется со скоростью вдоль линий магнитной индукции (угол между векторами и равен нулю или ), то по формуле (7.10) сила Лоренца равна нулю. И согласно первому закону Ньютона частица движется прямолинейно и равномерно. Если заряженная частица влетает в магнитное поле со скоростью , перпендикулярной вектору , то сила Лоренца (7.10) - постоянна по модулю, то есть согласно второму закону Ньютона эта сила создает центростремительное ускорение: 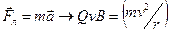, откуда

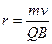(7.11)

- радиус окружности, по которой равномерно вращается частица в плоскости, перпендикулярной полю в этом случае.

Если скорость заряженной частицы (например, электрона Q < 0) направлена под углом 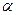к вектору (рис. 7.3), то её движение можно представить в виде суперпозиции двух движений: 1) равномерного прямолинейного движения вдоль поля со скоростью 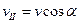; 2) равномерного вращения со скоростью 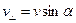по окружности в плоскости, перпендикулярной полю. Радиус окружности согласно (7.11) равен

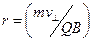. (7.12)

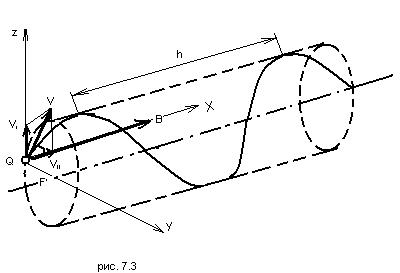
Рис. 7.3

В результате сложения обоих движений частица начинает двигаться по спирали (ось которой параллельна ). Период вращения частицы по спирали (время одного оборота) 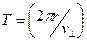и с учётом (7.12) получим 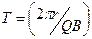. Шаг винтовой линии (путь, проходимый частицей вдоль поля за один оборот)

. (7.13)

Если скорость 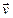заряженной частицы составляет угол 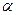с направлением неоднородного магнитного поля, индукция которого возрастает в направлении движения частицы, то и r и h спирали уменьшаются с ростом В. На этом эффекте основана фокусировка заряженных частиц в магнитном поле.