Циркуляция вектора магнитной индукции для магнитного поля в вакууме

Аналогично циркуляции вектора напряженности 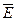электрического поля вводится понятие - циркуляция вектора магнитной индукции. Циркуляцией вектора 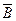по заданному замкнутому контуру называется интеграл

, (7.1)

где 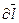- вектор элемента длины контура; 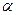- угол между векторам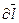и и 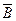; 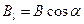- проекция 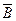на направление .

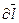В теоретической электродинамике доказывается теорема о циркуляции вектора 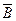(закон полного тока для магнитного поля в вакууме): циркуляция вектора 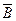по произвольному замкнутому контуру равна произведению магнитной постоянной на алгебраическую сумму токов, охватываемых этим контуром

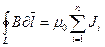. (7.2)

Здесь n - число проводников с токами, охватываемых контуром L. В дифференциальной форме для данной точки поля 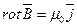, где 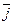- плотность тока в этой точке. Поэтому магнитное поле является вихревым в отличие от потенциального электростатического поля. Каждый ток учитывается столько раз, сколько он охватывается контуром. Положительным считается ток, направление которого связано с произвольно выбранным направлением обхода по контуру правилом правого винта. Ток противоположного направления считается отрицательным. Закон полного тока позволяет рассчитывать магнитные поля разной конфигурации, гораздо проще, чем с помощью закона Био-Савара-Лапласа в сочетании с принципом суперпозиции магнитных полей.

Проиллюстрируем это выводом формулы магнитного поля прямого тока (тока, текущего по тонкому прямому проводу бесконечной длины), перпендикулярного плоскости чертежа и направленного к нам (рис. 7.1). Возьмем в качестве произвольного замкнутого контура L окружность радиуса R. В каждой точке этого контура вектор 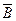одинаков по модулю и направлен по касательной к контуру L (окружность, которая одновременно и является линией магнитной индукции, то есть 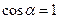). Циркуляция вектора (по закону полного тока) равна (7.2) 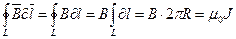, откуда окончательно получаем

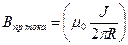. ( 7.3)

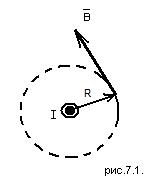
Рис. 7.1

Сравнивая выражение (2.3) и (7.2) для циркуляции векторов 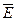и 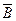можно увидеть принципиальную разницу. Циркуляция вектора 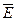электростатического поля всегда равна нулю, то есть электростатическое поле является потенциальным. Циркуляция же вектора 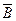магнитного поля не равна нулю. Такое поле называется вихревым. Таким образом теорема о циркуляции вектора 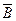имеет в учении о магнетизме такое же значение, как теорема Гаусса в электростатике, так как позволяет находить магнитную индукцию поля без использования закона Био-Савара-Лапласа.