Поток вектора магнитной индукции. Теорема Гаусса для магнитного поля. Работа по перемещению проводника с током и контура с током в магнитном поле

Потоком вектора магнитной индукции (магнитным потоком) через площадку 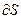называется скалярная величина равная

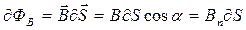, (7.14)

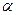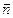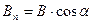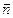где - угол между векторами и ; - проекция вектора на направление - нормали к площадке; 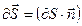- вектор, модуль которого равен площади площадки 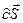, а направление которого совпадает с направлением 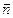нормали к площадке. В зависимости от знака 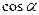поток может быть и положительным и отрицательным. Учитывая (6.4) при 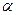=0 (cos 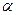= l) можно получить

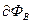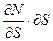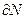~ ~ , (7.15)

то есть поток вектора магнитной индукции сквозь некоторую поверхность пропорционален числу линий вектора , пронизывающих рассматриваемую поверхность. Поток вектора сквозь конечную поверхность S соответственно равен

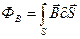. (7.16)

Для наиболее распространенного частного случая (плоская поверхность в однородном поле)

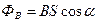. (7.17)

Единица магнитного потока в СИ: 1 Вебер [1Вб = 1Тл·м²].

Если рассматривать поток вектора сквозь замкнутую поверхность, то учитывая замкнутость линий вектора , любая из них пересечёт поверхность как минимум дважды (в общем случае чётное число раз). Согласно (7.14) и (7.15) одно из пересечений совпадает с положительной нормалью 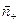, а другое с отрицательной 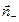. В итоге можно прийти к выводу, что поток вектора магнитной индукции через любую замкнутую поверхность равен нулю

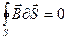. (7.18)

Это утверждение называется теоремой Гаусса для потока вектора магнитной индукции. В дифференциальной форме теорема Гаусса записывается 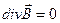. В качестве примера рассчитаем поток вектора через соленоид. Закон полного тока (7.2) позволяет получить выражение для магнитной индукции однородного поля внутри соленоида с сердечником с магнитной проницаемостью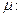

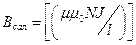. (7.19)

Магнитный поток через один виток соленоида площадью S равен Ф₁ = BS, а полный магнитный поток, сцепленный со всеми витками соленоида (и называемый потокосцеплением)

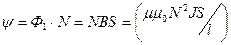. (7.20)

Как было рассмотрено выше, на проводник с током в магнитном поле действует сила Ампера. Незакреплённый проводник под действием этой силы будет перемещаться, то есть магнитное поле будет совершать работу.

Рассмотрим проводник длиной l с током J, помещённый в однородное магнитное поле (рис. 7.4), на который в соответствии с выражением (7.5) действует сила Ампера 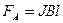. Направление этой силы определяется по правилу левой руки. Под действием этой силы проводник будет перемещаться из положения «1» в положение «2» на расстояние .

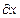В этом случае работа, совершённая магнитным полем равна

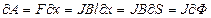, (7.21)

где 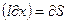- площадь, пересекаемая проводником при его перемещении в магнитное поле; 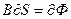- магнитный поток вектора , пронизывающий эту площадь.

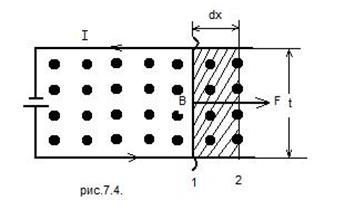
Рис. 7.4

Таким образом, работа по перемещению проводника с током в магнитном поле равна произведению силы тока на магнитный поток, пересечённый движущимся проводником. Эта работа совершается за счёт энергии источника, поддерживающего ток.

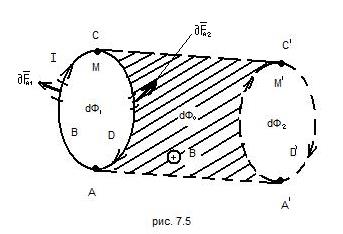
Рис. 7.5

Рассмотрим теперь перемещение замкнутого контура с постоянным током в магнитном поле (рис. 7.5). Контур М перемещается в плоскости чертежа и в результате бесконечно малого перемещения занимает положение М'. Мысленно разобьем контур М на два соединённых своими концами проводника ABC и CDA. Работа 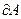, совершаемая силами Ампера по перемещению контура равна алгебраической сумме работ по перемещению проводников АВС 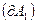и СDA 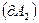. Силы, приложенные к участку CDA образуют с направлением перемещения острые углы (например, 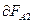см. рис.) и совершённая ими работа 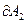> 0. Проводник CDA пересекает при своём движении поток 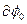сквозь заштрихованную поверхность (см. рис.) и поток 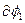, пронизывающий контур в его конечном положении (М'). Согласно (7.21) имеем

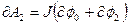. (7.22)

Силы, действующие на участок ABC контура (направление 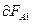см. на рис. 7.5) образуют с направлением пересечения тупые углы и совершённая ими работа, 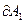< 0 . Проводник ABC пересекает при своем движении поток 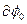(сквозь заштрихованную поверхность см. рис.) и поток 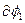, пронизывающий контур в его начальном положении. Согласно (7.22) получаем в данном случае

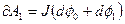. (7.23)

Элементарная работа по перемещению контура с учётом (7.22) и (7.23) может быть записана как 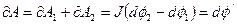- изменение магнитного потока, через площадь ограниченную контуром с током. Работа сил Ампера при конечном произвольном перемещении контура с током в магнитном поле, соответственно равна

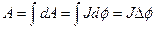, (7.24)

то есть работа по перемещению контура с током в магнитном поле равна произведению силы тока в контуре на приращение магнитного потока 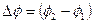, сцепленного с контуром.