Индукция магнитного поля соленоида

Для создания магнитного поля в технике используется соленоид – цилиндрическая катушка, состоящая из большого числа витков, равномерно намотанных на общий сердечник (рис. 4.5).

Рассмотрим соленоид длиной L, имеющий N витков, по которому течет ток I. Длину соленоида считаем во много раз большей диаметров его витков. Магнитное поле такого соленоида целиком сосредоточено внутри него и однородно. Снаружи соленоида поле мало и его практически можно считать равным нулю.

Величину индукции магнитного поля соленоида можно найти, складывая магнитные индукции полей, создаваемых каждым витком соленоида. Так как витки соленоида намотаны вплотную друг к другу, на длине dx сосредоточено 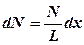витков. Суммарный ток, протекающий по кольцу, толщиной dx, равен 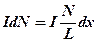. В точке, находящейся на оси соленоида каждое такое кольцо создает магнитное поле, согласно (4.7), равное:

.

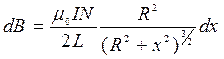Суммарное поле:

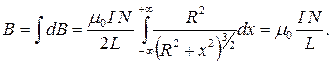(4.9)

При интегрировании соленоид считаем бесконечным. Как видно из (4.9) магнитное поле соленоида зависит от плотности намотки – числа витков на единицу длины соленоида .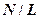

Магнитный поток

Потоком вектора магнитной индукции (магнитным потоком) через площадку dS называется скалярная физическая величина, равная:

dФ = В_ndS = Bcos α × dS, (4.10)

где В_n – проекция вектора В на направление, перпендикулярное к площадке dS; α – угол между вектором нормали nи вектором В.

Положительное направление нормали связано правилом правого винта с током, текущим по контуру, ограничивающему площадку dS. Магнитный поток Ф через произвольную поверхность S можно представить в виде:

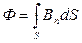. (4.11)