Внутренняя энергия. 1 страница
Любая термодинамическая система в каждом состоянии обладает запасом полной энергии 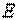 , которая состоит из внутренней энергии
, которая состоит из внутренней энергии 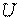 , зависящей от внутреннего состояния тела, и внешней энергии
, зависящей от внутреннего состояния тела, и внешней энергии 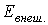 , связанной с движением тела как целого и положением его в каком-либо внешнем поле сил (например в поле сил тяжести), т. е.
, связанной с движением тела как целого и положением его в каком-либо внешнем поле сил (например в поле сил тяжести), т. е.
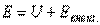
|
Если тело не движется, а влиянием внешнего поля сил можно пренебречь, то полная энергия будет представлять собой только внутреннюю энергию.
Любая термодинамическая система (рабочее тело) обладает запасом внутренней энергии, которая состоит из энергии хаотического (теплового) движения и взаимодействия молекул. Поскольку внутренняя энергия рабочего тела зависит от его массы, обычно интересуются значением внутренней энергии, отнесенной к 1 кг массы тела, — удельной внутренней энергией.
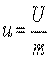 . .
|
В общем случае удельная кинетическая энергия теплового движения молекул состоит из удельной кинетической энергии поступательного, вращательного и колебательного движений молекул, зависящей только от температуры рабочего тела, и удельной потенциальной энергии взаимодействия молекул между собой, которая, в свою очередь, зависит от среднего расстояния между молекулами, т. е. от занимаемого рабочим телом объёма. Следовательно, в общем случае удельная внутренняя энергия рабочего тела зависит от его температуры 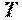 и удельного объема
и удельного объема 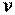 , являясь однозначной функцией этих параметров состояния:
, являясь однозначной функцией этих параметров состояния: 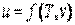 , или
, или
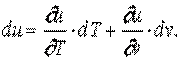 . .
|
Таким образом, важнейшим свойством удельной внутренней энергии рабочего тела является то, что она представляет собой однозначную функцию состояния тела, определяемого любой парой его основных параметров ( 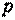 ,
, 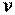 ,
, 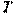 ), и сама может служить параметром состояния. Из этого свойства следует, что изменение удельной внутренней энергии не зависит от характера процесса, а определяется лишь начальным и конечным состояниями рабочего тела. Следовательно, бесконечно малое приращение удельной внутренней энергии является полным дифференциалом
), и сама может служить параметром состояния. Из этого свойства следует, что изменение удельной внутренней энергии не зависит от характера процесса, а определяется лишь начальным и конечным состояниями рабочего тела. Следовательно, бесконечно малое приращение удельной внутренней энергии является полным дифференциалом 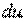 .
.
В идеальном газе силы взаимодействия между молекулами отсутствуют и удельная потенциальная энергия его равна нулю. Поэтому удельная внутренняя энергия идеального газа состоит только из удельной кинетической энергии движения молекул 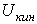 и определяется его температурой:
и определяется его температурой: 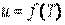 , или
, или
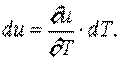
|
В замкнутом (круговом) процессе, в котором начальное и конечное состояния совпадают, изменение удельной внутренней энергии равно нулю.
Определять абсолютное значение удельной внутренней энергии в большинстве технических расчетов не требуется, так как обычно необходимо знать только ее изменение. Поэтому условно приписывают некоторому состоянию рабочего тела нулевое значение удельной внутренней энергии, а все расчеты ведут относительно этого значения.
Энтальпия.
Рассмотрим полную энергию газа, находящегося под давлением 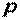 , создаваемым грузом массой
, создаваемым грузом массой 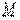 (рис. 1.1). В этом случае полная энергия
(рис. 1.1). В этом случае полная энергия 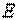 системы состоит из внутренней энергии газа
системы состоит из внутренней энергии газа 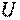 и потенциальной энергии груза, равной
и потенциальной энергии груза, равной 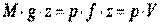 , где
, где 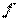 - площадь поперечного сечения поршня. Т. е.
- площадь поперечного сечения поршня. Т. е. 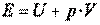 . Величина
. Величина 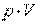 , зависящая от сил, действующих на поршень, получила название потенциальной энергии давления.
, зависящая от сил, действующих на поршень, получила название потенциальной энергии давления.

|
| Рис. 1.1. К определению энтальпии газа |
Таким образом, если газ находится в среде с давлением 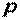 , то с любым состоянием его связана некоторая энергия
, то с любым состоянием его связана некоторая энергия 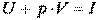 , получившая название энтальпии газа в данном состоянии. Выражение энтальпии для 1 кг газа (т. е. удельной энтальпии) имеет вид
, получившая название энтальпии газа в данном состоянии. Выражение энтальпии для 1 кг газа (т. е. удельной энтальпии) имеет вид
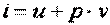 . .
|
Следовательно, удельная энтальпия, будучи зависимой от параметров состояния 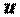 ,
, 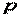 и
и 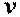 , также является параметром состояния. Поэтому изменение
, также является параметром состояния. Поэтому изменение 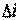 , как и изменение
, как и изменение 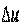 , не зависит от характера процесса, а определяется только начальным и конечным состояниями, т. е.
, не зависит от характера процесса, а определяется только начальным и конечным состояниями, т. е.
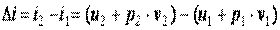 . .
|
Как однозначная функция состояния удельная энтальпия может быть представлена в виде функции любой пары основных параметров состояния.
Удельная энтальпия идеального газа, как и его удельная внутренняя энергия, является функцией только температуры. Действительно:
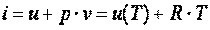 . .
|
Удельная энтальпия, как и удельная внутренняя энергия, выражается в джоулях на килограмм (Дж/кг).
Энтропия.
Кроме рассмотренных параметров, в термодинамике широко используется еще один калорический параметр состояния — энтропия 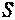 , введенный Клаузиусом в 1865 г. при анализе круговых процессов.
, введенный Клаузиусом в 1865 г. при анализе круговых процессов.
Энтропия — параметр состояния, дифференциал которого равен отношению бесконечно малого количества теплоты 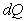 в элементарном обратимом процессе к абсолютной температуре
в элементарном обратимом процессе к абсолютной температуре 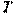 , постоянной на бесконечно малом участке процесса, т.е.
, постоянной на бесконечно малом участке процесса, т.е.
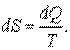
|
Если количество теплоты отнести к 1 кг вещества ( 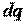 ), то получим удельную энтропию
), то получим удельную энтропию
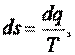
|
которая выражается в джоулях на килограмм-кельвин [Дж/(кг • К)].
1.5 Законы идеальных газов
1.5.1 Закон Бойля-Мариота
Бойль в 1662 году и Мариот в 1676 году обнаружили, что при 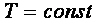
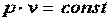 .
.
1.5.2.Закон Гей-Люссака
Гей-Люссак в 1802 году опытным путём установил, что при 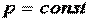
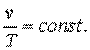
1.5.3.Закон Авогадро
В 1811 году Авогадро выдвинул гипотезу: одинаковые объёмы различных газов при одинаковых физических условиях содержат одинаковые количества молекул. Эта гипотеза, став после её доказательства законом, приводит к одному важному следствию, согласно которому при одинаковых физических условиях для любых газов произведение молекулярной массы газа на его удельный объём есть величина постоянная, т. е. 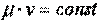 .
.
Напомним, что молекулярной массой называется количество вещества в граммах, численно равное его молекулярной массе. Например, молекулярная масса углерода равна 12 граммам, а кислорода - 32 граммам.
Произведение  представляет собой объём одного моля газа, который при нормальных физических условиях равен 22,4 м3.
представляет собой объём одного моля газа, который при нормальных физических условиях равен 22,4 м3.
Отметим, что нормальным физическим условиям соответствуют 760 мм рт. ст. и 00С, а нормальным техническим условиям - 735 мм рт. ст. и 100С.
1.6.Уравнение состояния
Сопоставление законов Бойля-Мариота и Гей-Люссака приводят к обобщённому закону Бойля-Гей-Люссака:
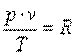 , ,
|
где 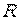 - характеристическая постоянная идеального газа (при нормальных физических условиях
- характеристическая постоянная идеального газа (при нормальных физических условиях 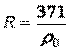
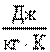 , где
, где 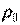 - плотность при нормальных физических условиях).
- плотность при нормальных физических условиях).
Это уравнение, полученное Клайпероном в 1834 году, называется уравнением состояния идеальных газов или уравнением Клайперона.
1.7.Работа изменения объёма газа
Выше отмечалось, что любое изменение состояния рабочего тела, которое происходит в результате его энергетического взаимодействия с окружающей средой, представляет собой термодинамический процесс. В общем случае энергообмен в термодинамическом процессе может осуществляться посредством работы L либо теплоты Q. Работа и теплота являются энергетическими характеристиками термодинамического процесса.
Механическая работа против внешних сил, связанная с изменением объема, определяется выражением
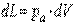 , ,
|
а удельная работа, т. е. работа, отнесенная к 1 кг вещества,— выражением
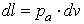 , ,
|
где 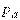 — абсолютное давление (потенциал механического взаимодействия),
— абсолютное давление (потенциал механического взаимодействия), 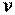 — удельный объем (координата механического взаимодействия).
— удельный объем (координата механического взаимодействия).
Для конечного процесса, при котором объем изменяется от 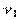 до
до 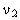 , общее выражение удельной термодинамической работы следует записать так:
, общее выражение удельной термодинамической работы следует записать так:
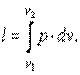
|
|
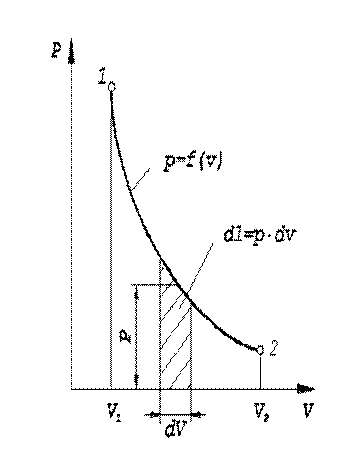
| Рис. 1.2. К вычислению работы в термодинамическом процессе |
В общем случае давление 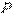 — величина переменная, зависящая от
— величина переменная, зависящая от 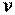 . Для определения интеграла должна быть известна зависимость между
. Для определения интеграла должна быть известна зависимость между 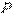 и
и 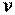 в данном процессе, т. е. надо знать уравнение процесса
в данном процессе, т. е. надо знать уравнение процесса 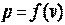 . Графически эта зависимость может быть изображена в
. Графически эта зависимость может быть изображена в 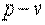 -координатах кривой 1-2 (рис. 1.2).
-координатах кривой 1-2 (рис. 1.2).
Очевидно, численно удельная работа будет зависеть от характера кривой процесса и изображается в 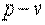 -координатах площадью, ограниченной кривой процесса, двумя ординатами и осью абсцисс.
-координатах площадью, ограниченной кривой процесса, двумя ординатами и осью абсцисс.
При вычислении интеграла обнаруживается, что если объём рабочего тела уменьшается, то величина интеграла отрицательна, и наоборот. Поэтому если рабочему телу сообщается потенциальная энергия путём его сжатия, то работа изменения объёма есть величина отрицательная. Если же рабочее тело совершает работу расширяясь, то работа изменения объёма - положительна.
Тема 2. ТЕПЛОЁМКОСТЬ ГАЗОВ
2.1.Массовая, объёмная и мольная удельные теплоёмкости
Известно, что подвод теплоты к рабочему телу или отвод теплоты от него в каком-либо процессе приводит к изменению его температуры. Отношение количества теплоты, подведенной (или отведенной) в данном процессе, к изменению температуры называется теплоемкостью тела (системы тел):
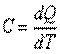 , ,
| (2.1) |
где 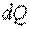 — элементарное количество теплоты;
— элементарное количество теплоты; 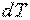 — элементарное изменение температуры.
— элементарное изменение температуры.
Теплоемкость численно равна количеству теплоты, которое необходимо подвести к системе, чтобы при заданных условиях повысить ее температуру на 1 градус. Так как единицей количества теплоты в СИ является джоуль, а температуры — градус К, то единицей теплоемкости будет Дж/К.
В зависимости от внешних условий и характера термодинамического процесса теплота 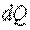 может либо подводиться к рабочему телу, либо отводиться от него. Учитывая, что система участвует в бесчисленном множестве процессов, сопровождающихся теплообменом, величина
может либо подводиться к рабочему телу, либо отводиться от него. Учитывая, что система участвует в бесчисленном множестве процессов, сопровождающихся теплообменом, величина 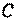 для одного и того же тела может иметь различные значения. В общем случае значение теплоёмкости
для одного и того же тела может иметь различные значения. В общем случае значение теплоёмкости 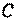 лежит в интервале от -∞ до +∞, то есть она может быть любой положительной или отрицательной величиной.
лежит в интервале от -∞ до +∞, то есть она может быть любой положительной или отрицательной величиной.
Поэтому обычно в выражении (2.1) при теплоёмкости 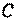 указывается индекс "x", который характеризует вид процесса теплообмена
указывается индекс "x", который характеризует вид процесса теплообмена
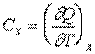 . .
| (2.2) |
Индекс "x" означает, что процесс подвода (или отвода) теплоты идет при постоянном значении какого-либо из параметров, например, давления 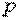 , объема
, объема 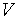 или других.
или других.
Ввиду того, что в термодинамике обычно рассматриваются квазистатические процессы теплообмена, теплоемкость 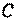 является величиной, относящейся к системе, которая находится в состоянии термодинамического равновесия. Таким образом, теплоемкости являются функциями параметров термодинамической системы. Для простых систем — это функции каких-либо двух из трех параметров:
является величиной, относящейся к системе, которая находится в состоянии термодинамического равновесия. Таким образом, теплоемкости являются функциями параметров термодинамической системы. Для простых систем — это функции каких-либо двух из трех параметров: 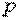 ,
, 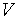 ,
, 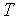 .
.
Опыты показывают, что количество теплоты, подведенное к рабочему телу системы или отведенное от него, всегда пропорционально количеству рабочего тела. Для возможности сравнения вводят, как известно, удельные величины теплоемкости, относя подведенную (или отведенную) теплоту количественно к единице рабочего тела.
В зависимости от количественной единицы тела, к которому подводится теплота в термодинамике, различают массовую, объемную и мольную теплоемкости.
Массовая теплоемкость — это теплоемкость, отнесенная к единице массы рабочего тела,
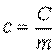 . .
|
Единицей измерения массовой теплоемкости является Дж/(кг • К). Массовую теплоемкость называют также удельной теплоемкостью.
Объемная теплоемкость — теплоемкость, отнесенная к единице объема рабочего тела,
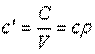 , ,
|
где 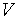 и
и 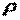 — объем и плотность тела при нормальных физических условиях.
— объем и плотность тела при нормальных физических условиях.
Объемная теплоемкость измеряется в Дж/(м3 • К).
Мольная теплоемкость — теплоемкость, отнесенная к количеству рабочего тела (газа) в молях,
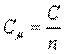 , ,
| (2.3) |
где 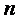 — количество газа в молях.
— количество газа в молях.
Мольную теплоемкость измеряют в Дж/(моль • К).
Массовая и мольная теплоемкости связаны следующим соотношением:
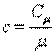
|
или
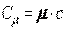 , ,
| (2.4) |
где 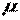 - молекулярная масса.
- молекулярная масса.
Объемная теплоемкость газов выражается через мольную как
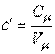
|
или
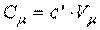 , ,
| (2.5) |
где 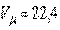 м3/моль — мольный объем газа при нормальных условиях.
м3/моль — мольный объем газа при нормальных условиях.
2.2.Средняя и истинная теплоёмкости
Учитывая, что теплоемкость непостоянна, а зависит от температуры и других термических параметров, различают истинную и среднюю теплоемкости. Истинная теплоемкость выражается уравнением (2.2) при определенных параметрах термодинамического процесса, то есть в данном состоянии рабочего тела. В частности, если хотят подчеркнуть зависимость теплоёмкости рабочего тела от температуры, то записывают её как 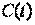 , а удельную – как
, а удельную – как 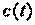 . Обычно под истинной теплоёмкостью понимают отношение элементарного количества теплоты, которое сообщается термодинамической системе в каком-либо процессе к бесконечно малому приращению температуры этой системы, вызванному сообщенной теплотой. Будем считать
. Обычно под истинной теплоёмкостью понимают отношение элементарного количества теплоты, которое сообщается термодинамической системе в каком-либо процессе к бесконечно малому приращению температуры этой системы, вызванному сообщенной теплотой. Будем считать 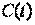 истинной теплоёмкостью термодинамической системы при температуре системы равной
истинной теплоёмкостью термодинамической системы при температуре системы равной 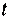 , а
, а 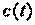 - истинной удельной теплоёмкостью рабочего тела при его температуре равной
- истинной удельной теплоёмкостью рабочего тела при его температуре равной 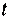 . Тогда среднюю удельную теплоёмкость рабочего тела при изменении его температуры от
. Тогда среднюю удельную теплоёмкость рабочего тела при изменении его температуры от 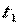 до
до 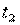 можно определить как
можно определить как
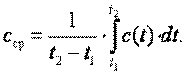
| (2.6) |
Обычно в таблицах приводятся средние значения теплоемкости 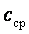 для различных интервалов температур, начинающихся с
для различных интервалов температур, начинающихся с 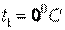 . Поэтому во всех случаях, когда термодинамический процесс проходит в интервале температур от
. Поэтому во всех случаях, когда термодинамический процесс проходит в интервале температур от 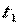 до
до 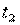 , в котором
, в котором 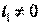 , количество удельной теплоты
, количество удельной теплоты 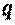 процесса определяется с использованием табличных значений средних теплоемкостей
процесса определяется с использованием табличных значений средних теплоемкостей 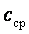 следующим образом:
следующим образом:
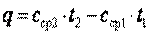 . .
| (2.7) |
Значения средних теплоемкостей 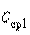 и
и 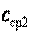 , находят по таблицам.
, находят по таблицам.
2.3.Теплоёмкости при постоянном объёме и давлении
Особый интерес представляют средние и истинные теплоемкости в процессах при постоянном объеме 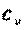 (изохорная теплоемкость, равная отношению удельного количества теплоты в изохорном процессе к изменению температуры рабочего тела dT) и при постоянном давлении
(изохорная теплоемкость, равная отношению удельного количества теплоты в изохорном процессе к изменению температуры рабочего тела dT) и при постоянном давлении 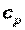 (изобарная теплоемкость, равная отношению удельного количества теплоты в изобарном процессе к изменению температуры рабочего тела dT).
(изобарная теплоемкость, равная отношению удельного количества теплоты в изобарном процессе к изменению температуры рабочего тела dT).
Для идеальных газов связь между изобарной и изохорной теплоёмкостями и устанавливается известным уравнением Майера 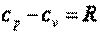 .
.
Из уравнения Майера следует, что изобарная теплоемкость больше изохорной на значение удельной характеристической постоянной идеального газа. Это объясняется тем, что в изохорном процессе ( 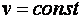 ) внешняя работа не выполняется и теплота расходуется только на изменение внутренней энергии рабочего тела, тогда как в изобарном процессе (
) внешняя работа не выполняется и теплота расходуется только на изменение внутренней энергии рабочего тела, тогда как в изобарном процессе ( 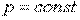 ) теплота расходуется не только на изменение внутренней энергии рабочего тела, зависящей от его температуры, но и на совершение им внешней работы.
) теплота расходуется не только на изменение внутренней энергии рабочего тела, зависящей от его температуры, но и на совершение им внешней работы.
Для реальных газов 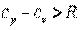 , так как при их расширении и
, так как при их расширении и 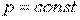 совершается работа не только против внешних сил, но и внутренняя работа против сил взаимодействия между молекулами газа, на что дополнительно расходуется теплота.
совершается работа не только против внешних сил, но и внутренняя работа против сил взаимодействия между молекулами газа, на что дополнительно расходуется теплота.
В теплотехнике широко применяется отношение теплоемкостей 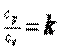 , которое носит название коэффициента Пуассона (показателя адиабаты). В табл. 2.1 приведены значения
, которое носит название коэффициента Пуассона (показателя адиабаты). В табл. 2.1 приведены значения 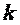 некоторых газов, полученные экспериментально при температуре 15 °С.
некоторых газов, полученные экспериментально при температуре 15 °С.
| Таблица 2.1 | |
| Газ | Показатель адиабаты |
| Гелий | 1,660 |
| Аргон | 1,667 |
| Окись углерода | 1,401 |
| Кислород | 1,398 |
| Водород | 1,408 |
| Азот | 1,41 |
| Водяной пар | 1,33 |
| Углекислый газ | 1,305 |
| Аммиак | 1,313 |
| Метан | 1,315 |
Теплоемкости 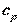 и
и 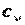 зависят от температуры, следовательно, и показатель адиабаты
зависят от температуры, следовательно, и показатель адиабаты 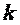 должен зависеть от температуры.
должен зависеть от температуры.
Известно, что с повышением температуры теплоёмкость 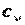 увеличивается. Поэтому с ростом температуры
увеличивается. Поэтому с ростом температуры 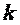 уменьшается, приближаясь к единице. Однако всегда остается больше единицы. Обычно зависимость показателя адиабаты от температуры выражается формулой вида
уменьшается, приближаясь к единице. Однако всегда остается больше единицы. Обычно зависимость показателя адиабаты от температуры выражается формулой вида
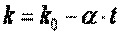 , ,
|
где 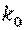 - значение коэффициента при 00 С;
- значение коэффициента при 00 С; 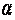 - коэффициент, принимающий для каждого газа своё постоянное значение.
- коэффициент, принимающий для каждого газа своё постоянное значение.
Кроме того, можно установить следующие широко использующиеся зависимости.
 , ,
| (2.8) |
и так как 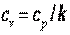
 . .
| (2.9) |
2.4. Таблицы теплоёмкости
Данные о теплоёмкостях различных газов приводятся в табличной форме. Обычно в таблицах приводят для различных температур значения мольной истинной и средней теплоёмкости при постоянном давлении и постоянном объёме. Указывают также средние массовые и объёмные теплоёмкости при постоянном объёме и постоянном давлении.
Мольная теплоёмкость указывается в кДж/(кмоль · 0С), массовая – в кДж/(кг · 0С), объёмная – в кДж/(м3 · 0С). При этом значения объёмной теплоёмкости относят к массе газа, заключённой 1 м3 его при нормальных физических условиях.
Для газов, массовая теплоёмкость которых зависит как от температуры, так и от давления, приводят значения удельного объёма и энтальпии 1 кг газа при различных давлениях и температурах. С такого рода зависимостями приходится иметь дело при изучении свойств водяного пара.
2.5.Теплоёмкость смеси рабочих тел (газовой смеси)
Дата добавления: 2016-03-27; просмотров: 1912;
