ЧАСТЬ 2. ТЕПЛОМАССООБМЕН

Тема 9. ТЕПЛОПРОВОДНОСТЬ

9.1.Основные понятия и определения

Теория теплопередачи, или теплообмена, представляет собой учение о процессах распространения теплоты в пространстве с неоднородным полем температур.

Существуют три основных вида теплообмена: теплопроводность, конвекция и тепловое излучение.

Теплопроводность — это молекулярный перенос теплоты между непосредственно соприкасающимися телами или частицами одного тела с различной температурой, при котором происходит обмен энергией движения структурных частиц (молекул, атомов, свободных электронов).

Конвекция осуществляется путем перемещения в пространстве не­равномерно нагретых объемов среды. При этом перенос теплоты не­разрывно связан с переносом самой среды.

Тепловое излучение характеризуется переносом энергии от одного тела к другому электромагнитными волнами.

Часто все способы переноса теплоты осуществляются совместно. Например, конвекция всегда сопровождается теплопроводностью, так как при этом неизбежно соприкосновение частиц, имеющих различные температуры.

Совместный процесс переноса теплоты конвекцией и теплопроводностью называется конвективным теплообменом. Частным случаем конвективного теплообмена является теплоотдача — конвективный теплообмен между твердой стенкой и движущейся средой. Теплоотдача может сопровождаться тепловым излучением. В этом случае перенос теплоты осуществляется одновременно теплопроводностью, конвекцией и тепловым излучением.

Многие процессы переноса теплоты сопровождаются переносом вещества — массообменном, который проявляется в установлении равновесной концентрации вещества.

Совместное протекание процессов теплообмена и массообменна называется тепломассообменном.

Теплопроводность определяется тепловым движением микрочастиц тела. В чистом виде явление теплопроводности наблюдается в твердых телах, неподвижных газах и жидкостях при условии невозможности возникновения в них конвективных токов.

Передача теплоты теплопроводностью связана с наличием разности температур тела. Совокупность значений температур всех точек тела в данный момент времени называется температурным полем. В общем случае уравнение температурного поля имеет вид:

,

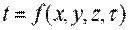(9.1)

где t — температура тела; х, у, z — координаты точки; τ — время. Такое температурное поле называется нестационарным и отвечает неустановившемуся режиму теплопроводности. Если температура тела не изменяется с течением времени, то температурное поле называется стационарным. Тогда

, .

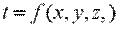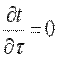(9.2)

Температура может быть функцией одной, двух и трех координат, соответственно температурное поле будет одно-, дву- и трехмерным. Наиболее простой вид имеет уравнение одномерного стационарного температурного поля:

; ; .

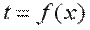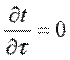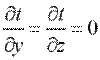Если соединить все точки тела с одинаковой температурой, то получим поверхность равных температур, называемую изотермической. Так как в определенной точке тела в данный момент времени может быть только одна температура, изотермические поверхности не пересекаются; все они либо замыкаются на себя, либо заканчиваются на границе тела. Пересечение изотермных поверхностей плоскостью дает на ней семейство изотерм. Интенсивность изменения температуры в каком-либо направлении характеризуется производной 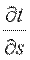, принимающей наибольшее значение в направлении нормали к изотермической поверхности

.

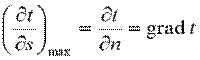(9.3)

Вектор называется температурным градиентом и является мерой интенсивности изменения температуры в направлении по нормали к изотермной поверхности. Направлен он в сторону возрастания температуры.

9.2.Закон Фурье

Согласно гипотезе Фурье, количество теплоты d²Q_τ, проходящее через элемент изотермической поверхности dF за промежуток времени dτ, пропорционально температурному градиенту :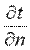

.

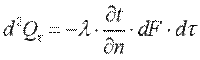(9.4)

Здесь множитель λ называется коэффициентом теплопроводности. Знак минус указывает на то, что теплота передается в направлении уменьшения температуры. Количество теплоты, прошедшее в единицу времени через единицу изотермической поверхности, называется плотностью теплового потока:

.

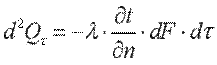(9.5)

Проекции вектора q на координатные оси соответственно:

; ; .

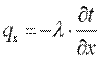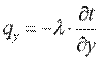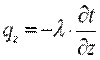Уравнения (9.4) и (9.5) являются математическим выражением основного закона теплопроводности — закона Фурье.

Количество теплоты, проходящее в единицу времени через изотермическую поверхность F, называется тепловым потоком:

.

(9.6)

Полное количество теплоты, прошедшее через эту поверхность за время τ, определится из уравнения

.

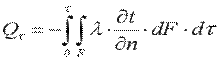(9.7)

9.3.Коэффициент теплопроводности

Коэффициент теплопроводности является физическим параметром вещества, характеризующим его способность проводить теплоту. Коэффициент теплопроводности определяется из уравнения (9.4):

.

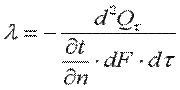(9.8)

Численно коэффициент теплопроводности равен количеству теплоты, проходящему в единицу времени через единицу изотермической поверхности при условии gradt=1. Его размерность Вт/(м·К). Значения коэффициента теплопроводности для различных веществ определяются из справочных таблиц, построенных на основании экспериментальных данных. Для большинства материалов зависимость коэффициента теплопроводности от температуры приближенно можно выразить в виде линейной функции

.

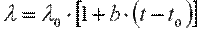(9.9)

где λ₀ — значение коэффициента теплопроводности при температуре t₀=0 ⁰С; b — постоянная, определяемая опытным путем.

Наихудшими проводниками теплоты являются газы. Коэффициент теплопроводности газов возрастает с увеличением температуры и составляет 0,006÷0,6 Вт/(м·К). Следует отметить, что верхнее значение относится к гелию и водороду, коэффициент теплопроводности которых в 5—10 раз больше, чем у других газов. Коэффициент теплопроводности воздуха при 0 ⁰С равен 0,0244 Вт/(м·К).

Для жидкости λ=0,07÷0,7 Вт/(м·К) и, как правило, уменьшается с увеличением температуры. Коэффициент теплопроводности воды с увеличением температуры возрастает до максимального значения 0,7 Вт/(м·К) при t=120 ⁰С и дальше уменьшается.

Наилучшими проводниками теплоты являются металлы, у которых λ=20÷418 Вт/(м·К). Самый теплопроводный металл — серебро. Для большинства металлов коэффициент теплопроводности убывает с возрастанием температуры, а также при наличии разного рода примесей. Поэтому коэффициент теплопроводности легированных сталей значительно ниже, чем чистого железа.

Материалы с λ<0,25 Вт/(м·К), обычно применяемые для тепловой изоляции, называют теплоизоляционными. Большинство теплоизоляционных и строительных неметаллических материалов имеют пористое строение, что не позволяет рассматривать их как сплошную среду.

9.4.Дифференциальное уравнение теплопроводности в плоской стенке при граничных условиях первого рода

9.4.1.Дифференциальное уравнение теплопроводности

Решение задач теплопроводности связано с определением поля температур и тепловых потоков. Для установления зависимости между величинами, характеризующими явление теплопроводности, воспользуемся методом математической физики, который рассматривает протекание физических процессов в произвольно выделенном из всего рассматриваемого пространства элементарном объеме и в течение бесконечно малого промежутка времени. Это позволяет пренебречь изменением некоторых величин и существенно упростить выкладки.

При выводе дифференциального уравнения теплопроводности считаем, что тело однородно и изотропно (то есть физические свойства тела не зависят от выбранного в нём направления), физические параметры λ, с(теплоемкость), и ρ (плотность) постоянны, внутренние источники теплоты равномерно распределены в теле. Под внутренними источниками теплоты понимаются тепловыделения, например, в тепловыделяющих элементах атомных реакторов, или при прохождении тока в электрических проводниках. Внутренние источники теплоты характеризуются величиной q_v — количеством теплоты, которое выделяется в единице объема в единицу времени.

В основу вывода положен закон сохранения энергии, согласно которому вся теплота, выделенная внутренними источниками dQ_вн и внесенная извне в элементарный объем путем теплопроводности dQ_m за время dτ, идет на изменение внутренней энергии вещества, содержащегося в этом объеме:

.

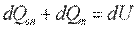(9.10)

Выделим в теле элементарный параллелепипед с ребрами dx, dy, dz (рис. 9.1). Количество теплоты, которое проходит путем теплопроводности внутрь выделенного объема в направлении оси ОX через элементарную площадку dy·dz за время dτ:

Рис. 9.1. К выводу дифференциального уравнения теплопроводности

.

На противоположной грани параллелепипеда температура получит приращение 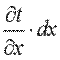и будет составлять .

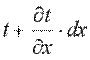Количество тепла, отведенного через эту грань:

.

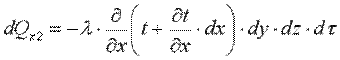Разница количества теплоты, подведенного к элементарному параллелепипеду и отведенного от него, представляет собой теплоту, внесенную путем теплопроводности в направлении оси ОX:

.

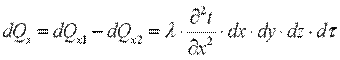Аналогично:

.

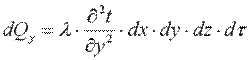Полное количество теплоты внесено в элементарный параллелепипед путем теплопроводности

.

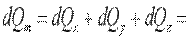
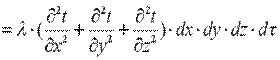Здесь произведение dx·dy·dz представляет собой объем элементарного параллелепипеда dv. Количество теплоты, которое выделилось в элементарном объеме за счет внутренних источников:

.

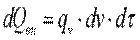Приращение внутренней энергии можно выразить через массу параллелепипеда ρ·dv, теплоемкость с и приращение температуры :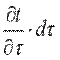

.

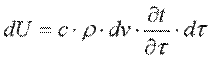Подставляя выражения для dQ_m, dQ_вн и dU в уравнение (9.10), после соответствующих сокращений получаем:

.

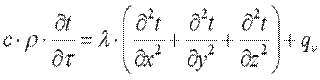(9.11)

Сумма вторых частных производных любой функции в математическом анализе носит название оператора Лапласа и обозначается следующим образом:

.

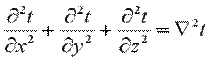Величину 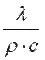называют коэффициентом температуропроводности и обозначают буквой a. В указанных обозначениях уравнение (9.11) примет вид:

.

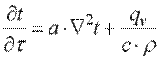(9.12)

Это уравнение называется дифференциальным уравнением теплопроводности или уравнением Фурье и лежит в основе математической теории теплопроводности. Коэффициент температуропроводности a является физическим параметром вещества. Из уравнения (9.12) следует, что изменение температуры во времени для любой точки тела пропорционально величине a.

9.4.2.Краевые условия

Дифференциальное уравнение (9.12) описывает в самом общем виде все без исключения задачи теплопроводности. Для решения конкретной задачи необходимо к дифференциальному уравнению присоединить математическое описание частных ее особенностей. Эти дополнительные данные, которые характеризуют конкретное единичное явление, называются краевыми условиями, или условиями однозначности.

Существуют различные условия однозначности: геометрические — характеризующие форму и размеры тела, в котором протекает про­цесс теплопроводности; физические — характеризующие физические свойства тела; временные — характеризующие распределение температуры тела в начальный момент времени; граничные — характеризующие взаимодействие тела с окружающей средой. Граничные условия в свою очередь бывают трех родов:

1) первого рода, задается распределение температуры на поверхности тела в функции времени;

2) второго рода, задается плотность теплового потока для всей поверхности тела в функции времени;

3) третьего рода, задаются температура окружающей среды t_ж и закон теплоотдачи между поверхностью тела и окружающей средой — закон Ньютона—Рихмана:

,

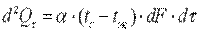(9.13)

где t_c — температура поверхности тела; α — коэффициент пропорциональности, называемый коэффициентом теплоотдачи, Вт/(м²·К). Коэф­фициент теплоотдачи численно равен количеству теплоты, отдаваемому или воспринимаемому единицей поверхности в единицу времени при разности температур между поверхностью тела и окружающей средой в один градус. Этот коэффициент учитывает все особенности явлении теплообмена, происходящие между поверхностью тела и окружающей средой. Плотность теплового потока, передаваемого от поверхности тела в окружающую среду,

.

(9.14)

Согласно закону сохранения энергии, эта теплота равна теплоте, подводимой к поверхности изнутри тела путем теплопроводности:

.

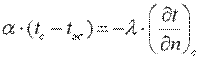Переписав последнее уравнение в виде:

,

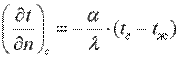(9.15)

получаем математическую формулировку граничных условий третьего рода. В результате решения дифференциального уравнения теплопроводности совместно с условиями однозначности можно найти температурное поле, а на основании закона Фурье — соответствующие тепловые потоки.

9.4.3.Теплопроводность через плоскую стенку при граничных условиях первого рода

Рис. 9.2. Однородная плоская стенка

Рассмотрим однородную плоскую стенку толщиной δ (рис. 9.2). На наружных поверхностях стенки поддерживаются постоянные температуры t_с1 и t_с2. Коэффициент теплопроводности стенки постоянен и равен λ. При стационарном режиме ( 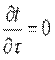) и отсутствии внутренних источников теплоты (q_v=0) дифференциальное уравнение теплопроводности примет вид:

.

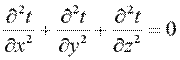(9.16)

При заданных условиях температура будет изменяться только в направлении, перпендикулярном плоскости стенки (ось Оx). В этом случае

,

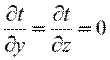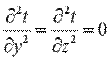
и дифференциальное уравнение теплопроводности перепишется в виде:

.

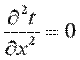(9.17)

Граничные условия первого рода запишутся следующим образом: при x=0 t=t_c1; при x=δ t=t_c2. Интегрируя уравнение (9.17), находим

.

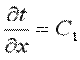После второго интегрирования получаем

.

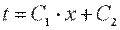(9.18)

Постоянные С₁ и С₂ определим из граничных условий: при x=0 t=t_c1, С₂=t_c1; при x=δ t=t_c2=С₁·δ+t_c1, отсюда 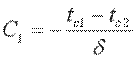. Подставляя значения С₁ и С₂ в уравнение (9.18), получим уравнение распределения температуры по толщине стенки:

.

(9.19)

Для определения плотности теплового потока, проходящего через стенку в направлении оси Оx, воспользуемся законом Фурье, согласно которому .

Учитывая, что 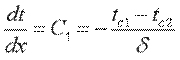, получим

.

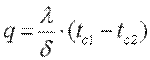(9.20)

Общее количество теплоты, которое передается через поверхность стенки F за время τ,

.

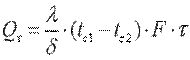(9.21)

Отношение 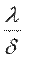называют тепловой проводимостью стенки, обратную ей величину 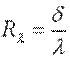- термическим сопротивлением теплопроводности. Поскольку величина λ зависит от температуры, в уравнения (9.20), (9.21) необходимо подставить коэффициент теплопроводности λ_с, взятый при средней температуре стенки.

Тема 10. КОНВЕКТИВНЫЙ ТЕПЛООБМЕН

10.1.Основные понятия и определения

Передача теплоты конвекцией осуществляется перемещением в пространстве неравномерно нагретых объемов жидкости или газов. В дальнейшем изложении обе среды объединены одним наименованием — жидкость. Обычно при инженерных расчетах определяется конвективный теплообмен между жидкостью и твердой стенкой, называемый теплоотдачей. Согласно закону Ньютона—Рихмана, тепловой поток Q от стенки к жидкости пропорционален поверхности теплообмена и разности температур между температурой твердой стенки t_c и температурой жидкости t_ж:

.

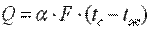(10.1)

Главная трудность расчета заключается в определении коэффициента теплоотдачи α, зависящего от ряда факторов: физических свойств омывающей поверхность жидкости (плотности, вязкости, теплоемкости, теплопроводности), формы и размеров поверхности, природы возникновения движения среды, скорости движения.

По природе возникновения различают два вида движения — свободное и вынужденное. Свободное движение происходит вследствие разности плотностей нагретых и холодных частиц жидкости, находящейся в поле действия сил тяжести; оно называется также естественной конвекцией и зависит от рода жидкости, разности температур, объема пространства, в котором протекает процесс.

Вынужденное движение возникает под действием посторонних побудителей (насоса, вентилятора, ветра). В общем случае наряду с вынужденным движением одновременно может развиваться и свободное. Относительное влияние последнего тем больше, чем больше разность температур в отдельных точках жидкости и чем меньше скорость вынужденного движения.

Движение жидкости может быть ламинарным или турбулентным. При ламинарном режиме частицы жидкости движутся послойно, не перемешиваясь. Турбулентный режим характеризуется непрерывным перемешиванием всех слоев жидкости. Переход ламинарного режима в турбулентный определяется значением безразмерного комплекса, называемого числом Рейнольдса:

,

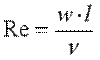где w – скорость движения жидкости; ν — коэффициент кинематической вязкости¹; l — характерный размер канала или обтекаемой стенки.

При любом режиме движения частицы жидкости, непосредственно прилегающие к твердой поверхности, как бы прилипают к ней. В результате вблизи обтекаемой поверхности вследствие действия сил вязкости образуется тонкий слой заторможенной жидкости, в пределах которого скорость изменяется от нуля на поверхности тела до скорости невозмущенного потока (вдали от тела). Этот слой заторможенной жидкости получил название гидродинамического пограничного слоя. Толщина этого слоя возрастает вдоль по потоку, так как по мере движения влияние вязкости распространяется все больше на невозмущенный поток. Однако и в случае турбулентного пограничного слоя непосредственно у стенки имеется очень тонкий слой жидкости, движение в котором носит ламинарный характер. Этот слой называется вязким или ламинарным подслоем.

Аналогично понятию гидродинамического слоя существует понятие теплового пограничного слоя — прилегающей к твердой поверхности области, в которой температура жидкости изменяется от температуры стенок t_с до температуры жидкости вдали от тела t_ж. В общем случае толщины гидродинамического и теплового пограничных слоев пропорциональны, а для газов практически равны.

Интенсивность переноса теплоты зависит от режима движения жидкости в пограничном слое. При турбулентном пограничном слое перенос теплоты в направлении стенки обусловлен турбулентным перемешиванием жидкости. Однако непосредственно у стенки, в ламинарном подслое теплота будет переноситься теплопроводностью. При ламинарном пограничном слое теплота в направлении стенки переносится только теплопроводностью.

10.2.Дифференциальные уравнения конвективного теплообмена

На основании рассмотренного выше представления о процессах переноса теплоты при движении жидкости вдоль твердой поверхности получим уравнение, описывающее процесс теплоотдачи на границах тела. Так как у поверхности твердого тела имеется слой неподвижной жидкости, то для этого слоя можно использовать закон Фурье. Принимая, что ось Оу направлена перпендикулярно поверхности, запишем

.

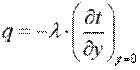Однако

.

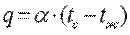Приравнивая эти уравнения получим

.

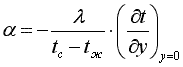(10.2)

Уравнение (10.2) называют дифференциальным уравнением теплоотдачи.

Если в дифференциальное уравнение теплопроводности подставить конвективное изменение температуры, обусловленное течением жидкости:

.

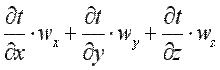где w_x, w_y и w_z – проекции скорости жидкости на координатные оси, то можно записать

.

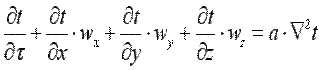(10.3)

Иными словами говоря, если через изучаемый нами элементарный объём движется со скоростью w некое температурное поле, то дифференциальное уравнение теплопроводности следует накладывать на это поле.

Для строго описания процессов конвективного теплообмена к дифференциальному уравнению (10.3) следует добавить уравнение (Навье-Стокса) движения вязкой жидкости, вытекающее из второго закона Ньютона, уравнение сплошности и неразрывности жидкости и учесть зависимость плотности жидкости от температуры. Такая система уравнений описывает большой класс явлений — процессы конвективного теплообмена между жидкостью и твердой стенкой. Эти уравнения должны быть дополнены условиями однозначности, характеризующими конкретные особенности той или иной рассматриваемой задачи.

10.3.Основы теории подобия

Ввиду сложности математического описания процессов конвективного теплообмена аналитическое решение дифференциальных уравнений с условиями однозначности оказывается возможным только в результате дополнительных упрощений, которые в значительной мере снижают практическую ценность полученных результатов. Поэтому многие зависимости для конкретных задач конвективного теплообмена получают экспериментальным путем. Распространение этих эмпирических зависимостей на другие конкретные явления может привести к грубым ошибкам.

Объединение математических методов с экспериментом с помощью теории подобия позволяет распространить результаты единичного опыта на целую группу явлений.

Понятие подобия, как известно, впервые введено в геометрии. Геометрически подобными называются такие фигуры, у которых сходственные (одноименные) стороны пропорциональны, а сходственные углы равны.

Понятие подобия распространяется на любое физическое явление. Физические явления считаются подобными, если они относятся к одному и тому же классу, протекают в геометрически подобных системах, и подобны все однородные физические величины, характеризующие эти явления. Однородными называются такие величины, которые имеют один и тот же физический смысл и одинаковую размерность. Таким образом, для подобных физических явлений в сходственных точках и в сходственные моменты времени любая величина φ′ первого явления пропорциональна величине φ′′ второго явления, т. е. φ′=c_φ·φ′′. При этом каждая физическая величина φ имеет свой множитель преобразования c_φ′ численно отличный от других.

Аналогично геометрическому подобию уравнения, описывающие подобные физические явления, после приведения их к безразмерному виду становятся тождественно одинаковыми. При этом в сходственных точках все одноименные безразмерные величины, в том числе и безразмерные параметры, будут равны.

Приведем к безразмерному виду дифференциальное уравнение теплоотдачи. Если ввести обозначение ϑ=t—t_c, то (10.2) можно записать в форме

.

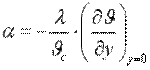(10.4)

Выберем какой-либо характерный геометрический размер l₀ и избыточную температуру стенки ϑ_c=t_с—t_ж в качестве величин приведения. Обозначим безразмерные величины 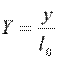и 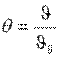, тогда y=l₀·Y и ϑ=ϑ₀·θ. Подставляя полученные выражения для у и ϑ в уравнение (10.4), запишем

.

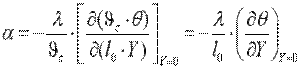Окончательно

.

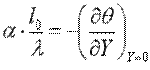(10.5)

Помимо безразмерной температуры θ и координаты Y, в уравнение входит безразмерный комплекс 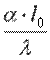, составленный из разнородных физических величин, характеризующих явление теплоотдачи. Согласно свойству подобных физических явлений, этот комплекс должен иметь одинаковые значения для всех подобных систем. Такие комплексы носят название чисел подобия.

Полученный безразмерный комплекс называется числом Нуссельта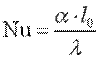

и представляет собой безразмерный коэффициент теплоотдачи.

Числа подобия, составленные только из заданных параметров математического описания задачи, называются критериями подобия. Анализ уравнений конвективного теплообмена позволяет получить следующие основные критерии подобия:

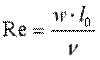— критерий Рейнольдса, характеризующий режим движения жидкости;

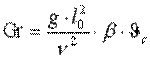— критерий Грасгофа, характеризующий подъемную силу, возникшую вследствие разности плотности жидкости. Здесь β - коэффициент объёмного расширения жидкости;

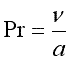— критерий Прандтля, определяющий физические свойства жидкости.

Критерии, составленные из величин, определяющих характер процесса, но не включающие искомых величин, называются определяющими, а критерии, включающие искомые величины, - неопределяющими. Так, при расчёте конвективного теплообмена критерий Nu не является определяющим, так как в него входит искомая величина α. Критерии же Re и Pr в этих же расчётах – определяющие.

10.4.Теоремы подобия

Основные положения теории подобия формулируются в виде трех теорем. Первая и вторая теоремы подобия формулируют основные свойства подобных между собой явлений, третья устанавливает признаки, по которым можно определить, подобны ли рассматриваемые явления.

В подобных явлениях все одноименные числа подобия (в том числе и критерии подобия) должны быть численно одинаковы. В этом заключается сущность первой теоремы подобия. Существует и такая формулировка этой теоремы: в сходственных точках подобных процессов одноимённые критерии должны иметь одинаковые значения. Здесь речь идёт о тех точках процессов, в которых определяются искомые величины.

На основании второй теоремы подобия зависимость между переменными, характеризующими какой-либо процесс, может быть представлена в виде зависимости между числами подобия. Функциональная зависимость между числами подобия называется уравнением подобия. При конвективном теплообмене уравнение подобия в общем случае имеет следующий вид:

.

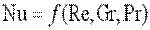(10.6)

Определенному численному значению критерия Рейнольдса соответствует бесчисленное количество значений каждого из параметров w, l₀, ν. Но каждому значению параметра соответствует конкретный единичный случай. Все это справедливо и для других критериев (Грасгофа, Прандтля). Следовательно, решение в форме (10.6) справедливо для бесчисленного количества тех единичных случаев, у которых одинаковы критерии Рейнольдса, Прандтля и Грасгофа, поэтому оно имеет обобщенный характер.

Сущность второй теоремы подобия хорошо определяется следующей формулировкой: определяющие и неопределяющие критерии подобных процессов связаны между собой уравнением подобия, которое является безразмерным решением рассматриваемой задачи, справедливым для всех подобных процессов.

Подобны те явления, у которых одноименные критерии подобия одинаковы — такова формулировка третьей теоремы подобия.

Теорию подобия можно рассматривать как учение о характерных для данного процесса обобщенных безразмерных переменных. Переход к таким переменным позволяет переносить полученные для единичного случая зависимости на группу подобных явлений. Область обобщения опытных данных ограничена условиями подобия, сформулированными третьей теоремой подобия.

На основании уравнений подобия можно определить значения числа Нуссельта и, следовательно, соответствующие значения коэффициента теплоотдачи .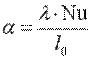

При решении уравнений подобия следует обращать внимание на определяющую температуру и определяющий геометрический размер. Определяющей температурой называется температура, по которой определяются значения физических параметров среды, входящих в числа подобия. Определяющим размером называется характерный линейный размер l₀, которым определяется развитие процесса. Например, для труб круглого сечения определяющим линейным размером является диаметр.

10.5.Уравнения подобия для различных случаев теплообмена

10.5.1.Теплоотдача при вынужденном омывании пластины

Учитывая, что изменение температуры происходит в тепловом пограничном слое, толщина которого пропорциональна толщине гидродинамического пограничного слоя, приближенно запишем

,

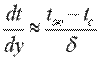(10.7)

где δ - толщина пограничного слоя.

Подставим это выражение в уравнение (10.2):

.

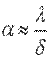(10.8)

Из (10.8) видно, что величина коэффициента теплоотдачи зависит от толщины пограничного слоя. В связи с увеличением δ коэффициент теплоотдачи уменьшается при удалении от носовой части пластины. Среднее значение коэффициента теплоотдачи:

в ламинарном пограничном слое (Re<4·10⁴)

;

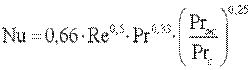(10.9)

в турбулентном пограничном слое (Re>4·10⁴)

.

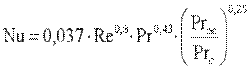(10.10)

В этих формулах в качестве определяющей принята температура жидкости вдали от тела, определяющего размера — длина пластины по направлению потока. Влияние направления теплового потока учитывается множителем 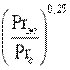. Заметим, что здесь и в дальнейшем индексы «ж» и «с» означают, что физические свойства жидкости выбирают соответственно по средней температуре жидкости и средней температуре стенки.

10.5.2.Теплоотдача при вынужденном движении в трубах

Интенсивность теплообмена в прямых гладких трубах зависит от режима течения потока, определяемого величиной Re. При движении жидкости в трубах развитый турбулентный режим течения устанавливается при значениях Re>10⁴; Re=2·10³÷1·10⁴ соответствует переходному режиму. При ламинарном движении происходит значительное изменение температуры по сечению трубы и соответственно изменение плотности текущей жидкости. Вследствие этого на вынужденное движение теплоносителя накладывается свободное движение. Интенсивность свободного движения характеризуется числом Грасгофа. Средний по длине трубы коэффициент теплоотдачи при вынужденном ламинарном движении жидкости в трубе, учитывающий влияние свободной конвекции, представляется в виде:

.

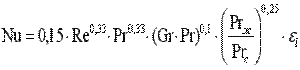(10.11)

Здесь определяющий геометрический размер — диаметр трубы d или эквивалентный диаметр канала любой формы; определяющая температура — средняя температура потока. Коэффициент ε_l, зависит от отношения l/d, где l — длина трубы. При l/d>50 ε_l=1. При l/d=1 ε_l=1,9.

При турбулентном режиме жидкость в потоке весьма интенсивно перемешивается и естественная конвекция практически не оказывает влияния на интенсивность теплообмена. Для определения среднего по длине трубы коэффициента теплоотдачи при развитом турбулентном движении (Re>10⁴) рекомендуется следующее уравнение подобия:

.

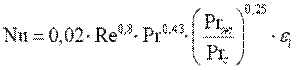(10.12)

Для потока в пределах Re=2·10³÷1·10⁴ лежит область переходного режима. Теплоотдача при этом режиме зависит от очень многих факторов, которые трудно учесть одним уравнением подобия. Приближенно коэффициент теплоотдачи в этой области можно оценить следующим образом. Наибольшее значение коэффициента теплоотдачи определится по формуле (10.12), а наименьшее с помощью уравнения

.

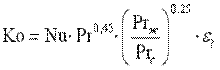(10.13)

Соответствующие значения числа Ко в зависимости от числа Re приведены ниже:

¹Коэффициент кинематической вязкости – это отношение коэффициента динамической вязкости к плотности жидкости. Коэффициент динамической вязкости – это коэффициент пропорциональности между силой трения слоёв жидкости друг о друга и их относительным смещением.

Тема 11. ТЕПЛООБМЕН ИЗЛУЧЕНИЕМ

11.1.Основные понятия и определения

Тепловое излучение представляет собой процесс распространения в пространстве внутренней энергии излучающего тела путем электромагнитных волн. Возбудителями этих волн являются материальные частицы, входящие в состав вещества. Для распространения электромагнитных волн не требуется материальной среды, в вакууме они распространяются со скоростью света и характеризуются длиной волны λ или частотой колебаний ν. При температуре до 1500 ⁰С основная часть энергии соответствует инфракрасному и частично световому излучению (λ=0,7÷50 мкм).

Следует отметить, что энергия излучения испускается не непрерывно, а в виде определенных порций — квантов. Носителями этих порций энергии являются элементарные частицы излучения — фотоны, обладающие энергией, количеством движений и электромагнитной массой. При попадании на другие тела энергия излучения частично поглощается ими, частично отражается и частично проходит сквозь тело. Процесс превращения энергии излучения во внутреннюю энергию поглощающего тела называется поглощением. Большинство твердых и жидких тел излучают энергию всех длин волн в интервале от 0 до ∞, то есть имеют сплошной спектр излучения. Газы испускают энергию только в определенных интервалах длин волн (селективный спектр излучения). Твердые тела излучают и поглощают энергию поверхностью, а газы — объемом.

Излучаемая в единицу времени энергия в узком интервале изменения длин волн (от λ до λ+dλ) называется потоком монохроматического излучения Q_λ. Поток излучения, соответствующий всему спектру в пределах от 0 до ∞, называется интегральным, или полным, лучистым потоком Q(Вт).

Интегральный лучистый поток, излучаемый с единицы поверхности тела по всем направлениям полусферического пространства, называется плотностью интегрального излучения (Вт/м²)

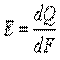
Отсюда

.

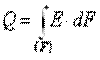Если величина Е одинакова для всех элементов поверхности F, то Q=E·F.

Плотность потока монохроматического излучения носит название спектральной интенсивности излучения J_λ.

Она связана с плотностью интегрального излучения уравнением:

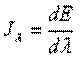
или

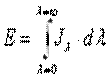
Каждое тело не только излучает, но и поглощает лучистую энергию. Из всего количества падающей на тело лучистой энергии E_пад (Q_пад) часть ее E_пог (Q_пог) поглощается, часть Е_от (Q_от) отражается и часть E_пр (Q_пр) проходит сквозь тело. Следовательно,

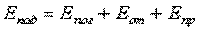
Обозначим

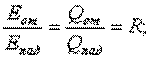
где А — коэффициент поглощения; R — коэффициент отражения, D — коэффициент пропускания. Тогда

А+R+D=1.

Если тело поглощает все падающие на него лучи, то есть A=1, R=О, D=0, оно называется абсолютно черным.

Если вся падающая на тело энергия отражается, то R=1, А=О, D=0. Если при этом отражение подчиняется законам геометрической оптики, тело называется зеркальным; при диффузном отражении, когда отраженная лучистая энергия рассеивается по всем направлениям, — абсолютно белым.

Если D=1, то A=0 и R=0. Такое тело пропускает все падающие на него лучи и называется абсолютно прозрачным.

В природе не существует абсолютно черных, белых и прозрачных тел.

Участвующее в лучистом теплообмене тело, помимо собственного излучения Е, определяемого свойствами излучающего тела и температурой, отражает падающую на него энергию, т. е.

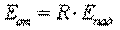
Сумма энергии собственного и отражательного излучения составляет эффективное излучение тела

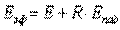
При расчете лучистого теплообмена между телами большое значение имеет результирующее излучение, представляющее собой разность между лучистым потоком, получаемым телом, и лучистым потоком, который оно испускает в окружающее пространство.

Для определения плотности потока результирующего излучения q_р полагая коэффициент пропускания тела равным нулю составим уравнение баланса энергии, проходящей через плоскости а—а и b—b, одна из которых расположена внутри, а другая снаружи тела вблизи его поверхности (рис. 11.1). Для плоскости а—а

Рис. 11.1. К составлению уравнения баланса энергии.

;

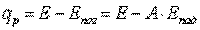(11.7)

для плоскости b—b

.

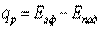(11.8)

Заметим, что величина q_р может быть положительной, отрицательной и равной нулю. Определим зависимость между результирующим и эффективным излучением.

Из (11.8)

,

(11.9)

из (11.7)

.

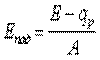(11.10)

Подставив выражение для E_пад в уравнение (11.9), получаем

.

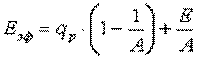(11.11)

Это уравнение широко используется при расчете лучистого теплообмена между телами.

11.2.Законы теплового излучения

Закон Планка устанавливает зависимость спектральной интенсивности излучения абсолютно черного тела J_oλ от длины волны и температуры:

,

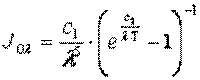(11.12)

где λ — длина волны излучения, м; Т — температура излучающего тела, К; c₁=3,74·10^-16 Вт·м²; c₂=1,44·10^-2 м·К; e – основание натуральных логарифмов.

Анализ выражения (11.12) показывает, что при λ=0 и λ=∞ J_oλ=0, а при некотором промежуточном значении - имеет максимум.

Для всех длин волн интенсивность излучения тем выше, чем выше температура.

Максимумы кривых с повышением температуры смещаются в сторону более коротких волн. (Закон Вина)