Внутренняя энергия. 2 страница
Теплоемкость газовой смеси вычисляется по составу газовой смеси и теплоемкостям отдельных газов, входящих в данную газовую смесь. Газовая смесь может быть задана массовым, объемным и молярным составом. Пусть смесь газов задана массовым составом, тогда масса смеси
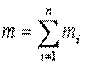 . .
| (2.10) |
где 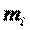 — масса i-го компонента, входящего в смесь.
— масса i-го компонента, входящего в смесь.
Очевидно, для увеличения температуры газовой смеси на 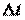 необходимо увеличить температуру на
необходимо увеличить температуру на 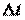 каждого газа этой смеси. При этом на нагревание каждого газа смеси необходимо затратить количество теплоты
каждого газа этой смеси. При этом на нагревание каждого газа смеси необходимо затратить количество теплоты 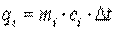 , где
, где 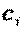 — массовая теплоемкость i-го газа смеси.
— массовая теплоемкость i-го газа смеси.
Теплоемкость газовой смеси определяется из уравнения теплового баланса
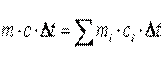 , ,
|
где 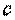 — теплоемкость газовой смеси.
— теплоемкость газовой смеси.
Разделив левую и правую части уравнения на 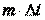 , получим
, получим
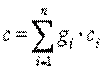 , ,
| (2.11) |
где 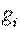 — массовая доля i-го газа, входящего в смесь.
— массовая доля i-го газа, входящего в смесь.
Из выражения (2.11) видно, что теплоемкость смеси газов, заданной массовыми долями (массовая теплоемкость смеси), равна сумме произведений массовых долей на массовую теплоемкость каждого газа.
С помощью аналогичных рассуждений можно найти сходные по структуре с полученным выражением выражения для объёмной и мольной теплоёмкостей газовой смеси.
Тема 3. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
3.1.Сущность первого закона термодинамики
Первый закон термодинамики является математическим выражением количественной стороны закона сохранения и превращения энергии в применении к термодинамическим системам. По этому закону теплота может превращаться в механическую работу или, наоборот, работа в теплоту в строго эквивалентных количествах. Это означает, что из данного количества теплоты в случае её полного превращения в работу получается строго определённое и всегда одно и то же количество работы, точно так же, как из данного количества работы при её полном превращении в тепло получается строго определённое и всегда одно и то же количество теплоты.
3.2. Аналитическое выражение первого закона термодинамики для цикла и разомкнутого процесса
Рассмотрим две системы: А и В (рис. 3.1). Предположим, что система А взаимодействует с системой В только в тепловом отношении. Пусть температура системы А выше температуры системы В (TA>TB), тогда разность температур TA-TB приведет к передаче теплоты от системы А к системе В. Запишем уравнение баланса энергии. Подводимая к системе В теплота 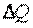 расходуется на изменение внутренней энергии
расходуется на изменение внутренней энергии 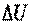 и на совершение всех видов работы
и на совершение всех видов работы 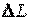 , то есть
, то есть
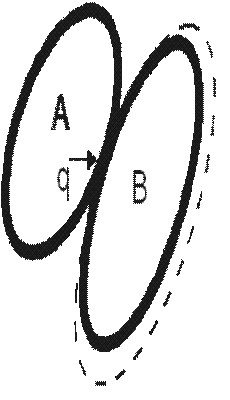
|
| Рис. 3.1. К выводу первого закона термодинамики |
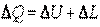 . .
| (3.1) |
Если затрачивается бесконечно малое количество теплоты, при этом совершается бесконечно малая работа и будет бесконечно малым изменение внутренней энергии, то уравнение (3.1) можно записать в виде
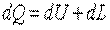 . .
| (3.2) |
Так как нас интересует только механическая работа, совершаемая при изменении объёма рабочего тела, то естественно интересоваться только той частью подводимого к системе В тепла, которое расходуется на изменение внутренней энергии и на совершение механической работы изменения объёма рабочего тела. Поэтому запишем
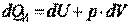 , ,
| (3.3) |
или
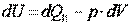 . .
| (3.4) |
Для 1 кг рабочего тела получим
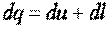 , ,
| (3.5) |
или
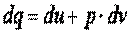 . .
| (3.6) |
Уравнения (3.5) и (3.6) являются математическим выражением первого закона термодинамики.
Для кругового процесса выражение первого закона термодинамики в интегральной форме запишется как
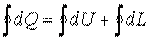 . .
| (3.7) |
Так как изменение внутренней энергии термодинамической системы не зависит от характера процесса и полностью определяется её начальным и конечным состояниями, то 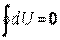 . Следовательно, все количество теплоты, подведенное к термодинамической системе или отведенное от нее в таком процессе, полностью расходуется на совершение системой внешней работы
. Следовательно, все количество теплоты, подведенное к термодинамической системе или отведенное от нее в таком процессе, полностью расходуется на совершение системой внешней работы
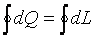 . .
| (3.8) |
То есть в круговом термодинамическом процессе теплота и работа взаимно превращаются в эквивалентных количествах. Если бы оказалось, что 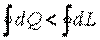 , то можно было бы осуществить вечный двигатель первого рода — двигатель, который совершал бы работу без затраты энергии.
, то можно было бы осуществить вечный двигатель первого рода — двигатель, который совершал бы работу без затраты энергии.
Таким образом, первый закон термодинамики, указывая на эквивалентность между теплотой и работой, свидетельствует о невозможности создания такой машины, которая бы производила работу, не затрачивая никакой энергии.
3.3. Уравнение первого закона термодинамики для потока газа
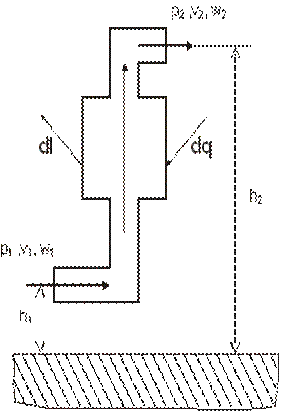
Уравнение первого закона для единицы массы стационарного потока (т. е. потока, параметры которого в любом сечении со временем не изменяются) можно вывести с помощью модели, показанной на рис. 3.2.
|
| Рис. 3.2. К выводу уравнения первого закона термодинамики для потока газа |
Здесь поток газа, получая теплоту dq, совершает техническую работу dl, а также работу за счет изменения его кинетической энергии d(w2/2) и работу против силы тяжести d(g*h) вследствие изменения его высоты над уровнем моря (h=h2-h1). Кроме того, имеет место работа вталкивания газа p1*v1 и выталкивания p2*v2. Их разность lпр=p2*v2-p1*v1 называют работой проталкивания. Учитывая сказанное можно записать закон сохранения энергии для движущегося рабочего тела
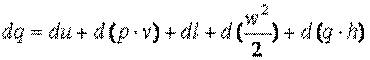
| (3.9) |
Здесь u – внутренняя энергия рабочего тела.
Так как по определению u+p*v=i, полученное выражение можно переписать следующим образом
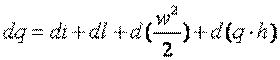
|
После интегрирования получим
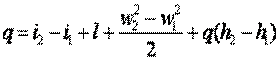
| (3.10) |
Выражение (3.10) и есть уравнение первого закона термодинамики для движущегося рабочего тела.
Тема 4 ТЕРМОДИНАМИЧЕСКИЕ ПРОЦЕССЫ
4.1 Алгоритм исследования термодинамических процессов
При исследовании термодинамических процессов применяют уравнение состояния идеальных газов и математическое выражение первого закона термодинамики.
При изучении термодинамических процессов идеальных газов необходимо:
1) определить уравнение кривой процесса в pv-диаграмме;
2) установить связь между основными термодинамическими параметрами;
3) вычислить изменение внутренней энергии рабочего тела по формуле, справедливой для всех процессов идеального газа,
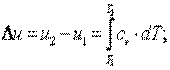
| (4.1) |
4) найти величину внешней (термодинамической) удельной работы по формуле

| (4.2) |
5) рассчитать количество теплоты, участвующей в термодинамическом процессе, по формуле
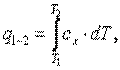
| (4.3) |
где cx – теплоёмкость процесса;
6) определить изменение энтальпии в термодинамическом процессе по формуле
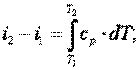
| (4.4) |
7) вычислить изменение энтропии в термодинамическом процессе по формуле, справедливой для всех процессов идеального газа,

| (4.5) |
В общем случае любые два термодинамических параметра из трех могут изменяться произвольно.
Изучение работы тепловых машин показывает, что наибольший интерес для практики представляют следующие основные процессы: при постоянном объеме (V=const); при постоянном давлении (р=const); при постоянной температуре (Т=const); при dq=0 (процесс, протекающий без теплообмена рабочего тела с окружающей средой) и политропный процесс, который при определенных условиях можно рассматривать в качестве обобщающего по отношению ко всем основным процессам.
Чтобы получить обобщенные и простые формулы, уравнения первого закона термодинамики рассматриваются для 1 кг идеального газа.
4.2 Термодинамические процессы
4.2.1 Изохорный процесс (v=const)
Такой процесс может совершаться рабочим телом, находящимся в цилиндре при неподвижном поршне, если к рабочему телу подводится теплота от источника теплоты (см. рис. 4.1) или отводится теплота от рабочего тела к холодильнику. При изохорном процессе выполняется условие dv=0 или v=const. Уравнение изохорного процесса получим из уравнения состояния идеального газа (см. 1.6) при v=const.
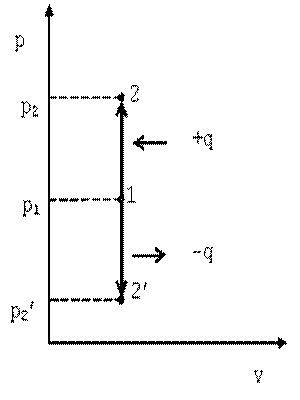
В pv-координатах график процесса представляет собой прямую линию, параллельную оси ординат p. Изохорный процесс может протекать с повышением давления (процесс 1-2) и с понижением (процесс 1-2’).
|
| Рис. 4.1 График изохорного процесса в p-v координатах |
Запишем для точек 1 и 2 уравнения состояния: p1·v=R·T1; p2·v=R·T2. Следовательно, для изохорного процесса
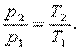
| (4.6) |
Приращение внутренней энергии газа
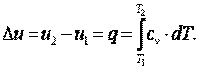
| (4.7) |
Работа газа
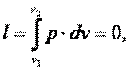
|
так как dv=0.
Энтальпия газа iv=u+p·v, а div=du+d(p·v)=du+p·dv+v·dp=du+v·dp. Поэтому
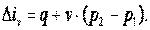
| (4.8) |
Энтропия 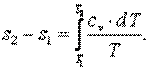
То есть
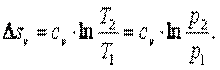
| (4.9) |
4.2.2 Изобарный процесс (p=const)
В p-v координатах график процесса представляет собой прямую линию параллельную оси абсцисс v (рис. 4.2). Изобарный процесс может протекать с увеличением объёма (процесс 1-2) и с его уменьшением (процесс 1-2’). Запишем для точек 1 и 2 уравнения состояния: p·v1=R·T1; p·v2=R·T2.
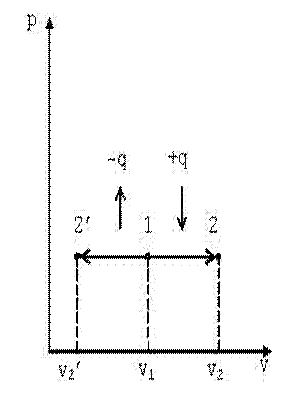
|
| Рис. 4.2. График изобарного процесса в p-v координатах |
Следовательно, для изобарного процесса
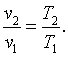
| (4.10) |
Приращение внутренней энергии газа 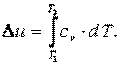 Работа газа
Работа газа 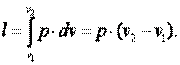
Так как p·v2=R·T2, а p·v1=R·T1, то l=R·(T2-T1). Следовательно, газовая постоянная имеет определённый физический смысл: это работа 1 кг газа в изобарном процессе при изменении температуры на один градус Кельвина.
Из выражения (4.3) следует, что в изобарном процессе q=cp·(T2-T1).
В соответствии с первым законом термодинамики для изобарного процесса можно записать
dq=du+p·dv= du+d(p·v)=di
Поэтому в изобарном процессе
di=q=cp·(T2-T1)
Из соотношений, характеризующих изобарный процесс, вытекает уравнение Майера.
Так как
dq=cp·dT=cv·dT+dl=cv·dT+R·dT,
то R=cp-cv.
Используя выражение (4.5), можно показать, что в изобарном процессе энтропия газа

| (4.11) |
4.2.3 Изотермический процесс (T=const)
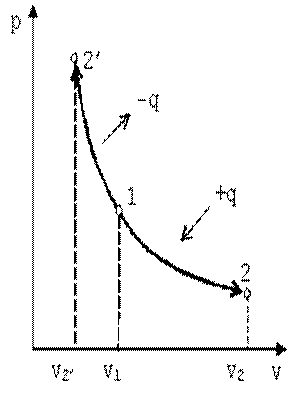
В p-v координатах график процесса изображается равнобокой гиперболой (рис. 4.3). Изотермический процесс может протекать как с увеличением объёма (процесс 1-2), так и с уменьшением объёма (процесс 1-2’).
|
| Рис. 4.3. График изотермического процесса в p-v координатах |
Запишем для точек 1 и 2 уравнения состояния p1·v1=R·T; p2·v2=R·T. Следовательно, для изотермического процесса p1·v1=p2·v2=const.
Приращение внутренней энергии газа
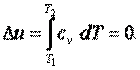
|
Работа газа

| (4.12) |
Теплота, подводимая в процессе
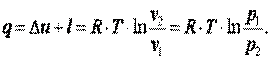
| (4.13) |
Энтальпия газа Δi=Δu+Δ(p·v)=0.
Изменение энтропии газа вычисляется по формуле

| (4.14) |
4.2.4 Адиабатный процесс
Адиабатный процесс – это процесс, при котором рабочее тело не обменивается теплотой с окружающей средой (dq=0). Для получения графика процесса в p-v координатах выполним некоторые преобразования.
В соответствии с первым законом термодинамики
dq=cv·dT+p·dv=c·dT,
где с – теплоёмкость термодинамического процесса.
Тогда можно записать, что
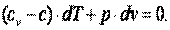
| (4.15) |

| (4.16) |
Продифференцируем уравнение состояния идеального газа и запишем
Так как R=cp-cv, то выражение (4.15) можно переписать с учётом (4.16) следующим образом:
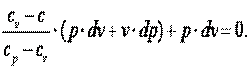
| (4.17) |
Выполним преобразования выражения (4.17).
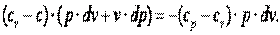
| |
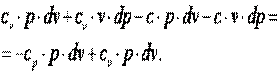
|
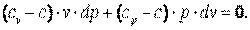
| (4.18) |
Разделим выражение (4.18) на (cv-c)·p·v и получим:

| (4.19) |
Обозначим 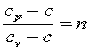 , тогда
, тогда
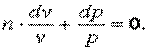
|
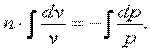
|
потенциируем
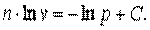
|
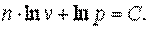
| |

|
Следовательно
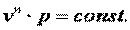
| (4.20) |
В адиабатном процессе dq=0, то есть c·dT=0. Поэтому c=0. Значит в адиабатном процессе 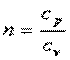 . Эту величину принято обозначать буквой
. Эту величину принято обозначать буквой 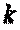 и называть показателем адиабаты.
и называть показателем адиабаты.
Поэтому в p-v координатах адиабатный процесс изображается неравнобокой гиперболой vk·p=const (рис. 4.4). Так как k>1, то адиабата проходит круче гиперболы. Адиабатный процесс может протекать как с увеличением объёма (процесс 1-2), так и с уменьшением объёма (процесс 1-2’).

| |
| Рис. 4.4. График адиабатного процесса в p-v координатах |
Запишем для точек 1 и 2 уравнения состояния p1·v1=R·T1; p2·v2=R·T2. Так как в адиабатном процессе p1·v1k=p2·v2k, то
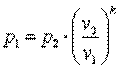 ,
, 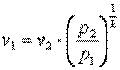 ,
, 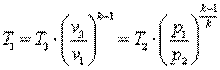 .
.
Приращение внутренней энергии газа  .
.
Так как 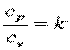 , а
, а 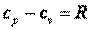 , то
, то 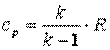 , а
, а  .
.
Поэтому
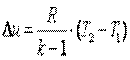
| (4.21) |
Работа газа в адиабатном процессе выполняется за счёт его внутренней энергии. Так как в адиабатном процессе отсутствует обмен теплотой с окружающей средой, то в соответствии с первым законом термодинамики имеем l+Δu=0 или l=-Δu. Поэтому

|
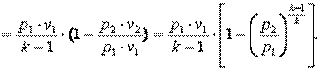
| (4.22) |
Изменение энтальпии газа в адиабатном процессе может быть определено исходя из следующих соображений:
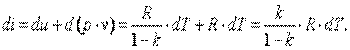
|
Так как  , то в итоге получим
, то в итоге получим
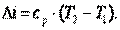
| (4.23) |
Энтропия газа в адиабатном процессе не изменяется, так как dq=0. Поэтому в T-s координатах адиабатный процесс изображается прямой линией, параллельной оси температур.
4.2.5 Политропный процесс
Политропным процессом называется любой произвольный процесс изменения состояния рабочего тела, происходящий при постоянной теплоёмкости сп.
В политропном процессе dq=cп·dT.
Для получения графика политропного процесса в p-v координатах будем придерживаться тех же рассуждений, что и при получении графика адиабатного процесса. Заменим в соотношениях, полученных при изучении адиабатного процесса, обозначение теплоёмкости с на сп и обнаружим, что p·vn=const, а 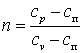 .
.
В дальнейшем всё, что написано об адиабатном процессе, можно распространить на описание политропного процесса, заменяя в выражениях k на n.
Покажем, что адиабатный процесс делит все процессы на две группы: на процессы, в которых теплоёмкость больше нуля, и на процессы, в которых теплоёмкость меньше нуля.
Так как 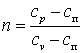 , то можно записать
, то можно записать
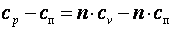 ;
;  ;
; 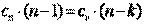 ;
;  .
.
Из последнего выражения видно, что при n>k cп>0, а при k>n>1 cп<0.
В заключение отметим, что все рассмотренные ранее процессы – это частные случаи политропного процесса.
При n=k имеем адиабатный процесс.
При n=0 имеем р1·v10=р2·v20, то есть изобарный процесс (p1=p2).
При n=1 имеем р1·v1= р2·v2, то есть изотермический процесс.
При n=∞ имеем 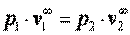 или
или 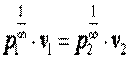 , что равносильно
, что равносильно 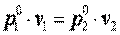 или
или 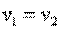 , то есть изохорный процесс.
, то есть изохорный процесс.
Тема 5 ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ
5.1.Сущность и формулировки второго закона термодинамики
Если исходить из первого закона термодинамики, то можно допустить протекание любого процесса, который не противоречит закону сохранения энергии. В частности, при теплообмене можно было бы предположить, что теплота может передаваться как от тела с большей температурой к телу с меньшей температурой, так и наоборот. При этом согласно первому закону термодинамики накладывается только одно условие: чтобы количество теплоты, отданной одним телом, равнялось количеству теплоты, принятой другим телом.
Между тем, из опыта известно, что теплота всегда самопроизвольно передается только от более нагретых тел к менее нагретым. Самопроизвольный или естественный процесс теплообмена обладает свойством направленности в сторону тел с более низкой температурой. Причём он прекращается при достижении равенства температур участвующих в теплообмене тел. Однако, возможен и обратный, не самопроизвольный (или противоестественный) процесс передачи теплоты от менее нагретых тел к более нагретым (например, в холодильных установках), но для осуществления его требуется подвод энергии извне как бы для компенсации протекания процесса.
Констатация этой особенности теплоты, проявляющейся в процессе ее передачи, является одной из сторон сущности второго закона термодинамики, который Р. Клаузиус (1850 г.) сформулировал так: теплота не может сама собой переходить от менее нагретого тела к более нагретому, т. е. некомпенсированный переход теплоты от тела с меньшей температурой невозможен.
Дата добавления: 2016-03-27; просмотров: 1223;
