Условная вероятность. Умножение вероятностей
Пример: На складе – 400 электрических лампочек, изготовленных на двух заводах (75 % – на первом, 25 % – на втором). Пусть на 1 заводе – 83 % соответствует стандарту, на 2 заводе – 63 %. Определим вероятность того, что случайно взятая со склада лампочка соответствует требованиям стандарта.
Решение. Всего на 1–м заводе изготавливают 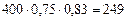 стандартных лампочек. На втором заводе –
стандартных лампочек. На втором заводе –  . Т.е. всего 249+63=312 стандартных лампочек. Так как выбор любой лампочки следует считать равновозможным, то имеем 312 благоприятствующих случаев из 400, и поэтому
. Т.е. всего 249+63=312 стандартных лампочек. Так как выбор любой лампочки следует считать равновозможным, то имеем 312 благоприятствующих случаев из 400, и поэтому
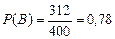 ,
,
где событие В состоит в том, что выбранная на любом из заводов лампочка стандартна.
Но если известно, что выбранная лампочка изготовлена на первом заводе (событие А1), то вероятность того, что она стандартна, будет не 0,78, а 0,83.
Такого рода вероятность, т.е. вероятность события В при условии, что имеет место событие А, называют условной вероятностью события В при условии наступления события А и обозначается РА(В).
Вероятность совмещения событий А и В равна произведению вероятности одного из событий на условную вероятность другого в предположении, что первое имело место
Р(А и В) = Р(А)РА(В).
Это так называемая теорема умножения.
Совмещение событий А и В – это наступление каждого из них, т.е. наступление как события А, так и события В.
Так как события А и В равноправны, то поменяв их местами:
Р(А и В) = Р(А)РВ(А) или
Р(А)РА(В) = Р(В)РВ(А).
Пример. В продукции предприятия признаются годными (событие А) 96 % изделий. К первому сорту (событие В) оказываются принадлежащими 75 изделий из каждой сотни годных. Определить вероятность того, что произвольно взятое изделие будет годным и принадлежит к первому сорту.
Искомая вероятность есть вероятность совмещения событий А и В. По условию: Р(А) = 0,96, РА(В) = 0,75, тогда Р(А и В) = 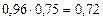 .
.
Два события называются независимыми, если вероятность одного из них не изменяется в результате того, наступило или не наступило другое.
Пример: повторное бросание монеты (Р =  независимо от того, выпал или не выпал герб в первом случае). Условие независимости событий А и В:
независимо от того, выпал или не выпал герб в первом случае). Условие независимости событий А и В:
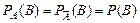 или
или
 .
.
Для независимых событий теорема умножения формулируется следующим образом. Если события А и В независимы, то вероятность их совмещения равна произведению вероятностей этих событий Р(А и В) = Р(А)Р(В).
Полная вероятность
Пусть события Н1, Н2,…, Нn образуют полную группу событий и при наступлении каждого из них (Нi) событие А может наступить с некоторой условной вероятностью 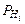 (А). Какова будет при этом вероятность наступления события А?
(А). Какова будет при этом вероятность наступления события А?
В соответствии с теорией умножения найдем, что вероятность наступления А при условии Н1, Н2,…, Нn:
Р(Н1 и А) = Р(Н1) 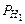 (А)
(А)
…………………………..
Р(Нn и А) = Р(Нn) 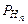 (А).
(А).
По теореме сложения (события Н1, Н2,… несовместны):
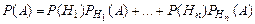 или
или
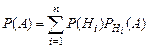 – это так называемая формула полной вероятности.
– это так называемая формула полной вероятности.
Пример. При разрыве снаряда образуются крупные, средние и мелкие осколки, причем число крупных осколков составит 0,1 их общего числа; средних – 0,3; мелких – 0,6.
При попадании в танк крупный осколок прибивает броню с вероятностью 0,9; средний – 0,3; мелкий – 0,1.
Какова вероятность того, что попавший в броню осколок пробьет ее?
| Р(Н1) = 0,1 Р(Н2) = 0,3 Р(Н3) = 0,6 | 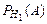 = 0,9 = 0,9
 = 0,3 = 0,3
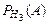 = 0,1 = 0,1
|
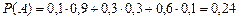 .
.
1.3. Случайные величины
Под случайной величиной понимается величина, принимающая в результате опыта какое–либо числовое значение из множества возможных значений.
Примеры: 1) Число выстрелов, произведенных до первого попадания в цель (любое целое положительное число).
2) Расстояние от центра мишени до точки попадания (любое положительное число или 0).
Случайная величина, принимающая конечное число или последовательность различных значений, называется дискретной случайной величиной (пример 1).
Случайная величина принимающая все значения из некоторого интервала, называется непрерывной случайной величиной (пример 2).
Чтобы охарактеризовать дискретную случайную величину, прежде всего необходимо указать возможные ее значения. Однако этого недостаточно: нужно еще знать, насколько часто принимаются различные значения этой величины, что лучше всего характеризовать вероятностью отдельных ее значений. Иначе говоря, для случайной величины Х следует указывать не только ее значения x1, x2,…, xn, но и вероятности событий X = xi, рi = P(X = xi), (i = 1,2,…,n) состоящих в том, что случайная величина Х приняла значение хi.
Если перечислены все возможные значения X, то события X = xi не только несовместны, но и единственно возможны, так что сумма заданных вероятностей рi должна равняться единице.
Соотношение, устанавливающее связь между значениями случайной величины и вероятностями этих значений, называется законом распределения случайной величины.
Для дискретной случайной величины закон распределения удобно записывать в виде таблицы, причем  .
.
| x1 | x2 | … | хi | … | xn |
| р1 | р2 | … | рi | … | рn |
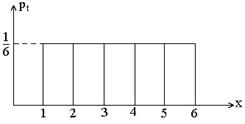
Иногда этот закон задают в виде графика: по оси абсцисс откладывают возможные значения случайной величины Х, а по оси ординат – соответствующие значения вероятностей. Получаемая при этом ломаная линия называется многоугольником распределения.
Пример: Х – число очков, выпадающих на игральной кости. Возможные значения 1,…,6 равновероятны.
Закон распределения:
| хi | ||||||
| рi | 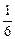
| 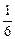
| 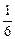
| 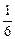
| 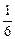
| 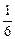
|
Многоугольник распределения:
Дата добавления: 2016-03-27; просмотров: 1472;
