Функции распределения случайной величины

Закон распределения не всегда можно задать таблицей. Например, для непрерывной случайной величины невозможно перечислить все ее значения. Поэтому ее характеризуют не вероятностями отдельных значений, как дискретную, а вероятностями того, что случайная величина принимает значения из определенного интервала, т.е. вероятностями неравенств вида 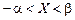. (Можно и для дискретных).

Обычно говорят о вероятности неравенства 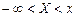, т.е. вероятности того, что случайная величина принимает значение, меньшее х. Эта вероятность Р(X < x) является, очевидно, функцией х. Обозначим ее F(x)

.

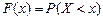Функцию F(x) называют интегральным законом распределения или функцией распределения случайной величины X.

1.3.1.1. Свойства функции распределения

Пусть X – случайная величина, x₁ и x₂ – две произвольные точки, причем x₁<x₂. Сравним значения функции F(х) в этих точках. Так как событие X<x₁ влечет событие X<x₂, то ясно, что

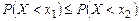, или

по определению функции распределения,

.

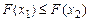Таким образом, функция распределения для любой случайной величины всегда является монотонно неубывающей.

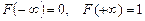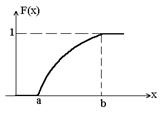
Очевидно , откуда следует, что 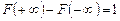. Так как F(х) – монотонна и заключена между 0 и 1, то график функции y = F(x) имеет две горизонтальные асимптоты: у = 0 при х ® 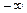и у = 1 при х® .

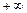Если все значения случайной величины принадлежат интервалу (а, b), то слева от точки «а» имеем F(x) = 0, а справа от «b» – функция F(x) = 1.

1.3.1.2. Функция распределения для дискретной случайной

величины

Функция распределения для дискретной случайной величины

,

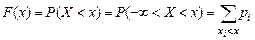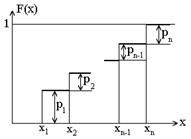
где суммирование распространяется на значения х_i, удовлетворяющие неравенству х_i < x. В промежутке между двумя последовательными значениями Х функция F(x) постоянна. При переходе же аргумента х через возможное значение случайной величины х_i функция F(x) скачком возрастает на величину р_i = P(X = x_i), так что х_i будет точкой разрыва первого рода функции F(x), поэтому функция распределения для дискретной случайной величины будет ступенчатой функцией.

Т.о., для конечно–значной величины функция распределения F(x) равна сумме вероятностей всех допустимых значений, меньших, чем х.

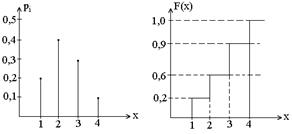
Пример. Смешаны шарики (100) различной крупности, среди которых 20 шариков диаметром 1 см; 40 шариков – 2 см; 30 шариков – 3 см и 10 шариков – 4 см.

Определить вероятности извлечения шарика определенной крупности и построить F(x), если х – крупность шарика.

1.3.1.3. Функция распределения непрерывной случайной

величины

Пусть Х – непрерывная случайная величина с известной функцией распределения F(х).

Найдем вероятность того, что Х заключена в пределах a < X < b. Пользуясь теоремой сложения вероятностей:

Р(Х<b)=P(X<a)+P(a<X<b),

Откуда

P(a<X<b)=Р(Х<b) ).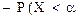

Исходя из определения функции распределения:

.

Определим вероятность Р(Х = a):

.

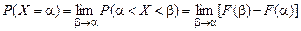Если функция F(х) непрерывна, то последний предел равен нулю: Р(Х = a) = 0.

Т.е., если функция распределения случайной величины непрерывна, то вероятность того, что случайная величина примет заранее заданное значение, равна нулю, но это событие не является невозможным.