Классическое определение вероятности. Имеется система конечного числа событий А1, А2, , Аn.
Имеется система конечного числа событий А1, А2, …, Аn.
1) Эти события попарно несовместны, т.е. для любых двух событий появление одного исключает появление другого.
2) События А1, А2, …, Аn – единственно возможны.
3) События равновозможны, т.е. не существует никаких объективных причин, вследствие которых одно из них могло бы наступать чаще, чем какое–либо другое.
Пусть имеется событие А, которое наступает при появлении некоторых из наших «элементарных» событий А1, А2, …, Аm и не наступает при появлении других. Будем говорить в таком случае, что те из «элементарных» событий Аi, при наступлении которых наступает также событие А, благоприятствуют событию А.
Допустим, что из общего числа n рассматриваемых событий А1, А2, …, Аn событию А благоприятствует m из них. Тогда вероятностью события А называется отношение числа событий, благоприятствующих событию А, к общему числу всех равновозможных событий.
Если Р(А) – вероятность А, то 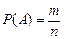 .
.
Пример: бросание игральной кости. (А1 – выпадение единицы, А2 – выпадение двойки и т.д.)
Р(А1) = Р(А2) =…= Р(А6) = 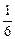 , так как m = 1, n = 6.
, так как m = 1, n = 6.
Если событие А означает появление четного числа очков, то ему благоприятствуют события А2, А4, А6, состоящие в появлении 2–х, 4–х, 6–и очков. Таким образом, для события А: m = 3 и Р(А) = 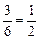 .
.
Дата добавления: 2016-03-27; просмотров: 585;
