Средние значения случайных величин

Предположим, что Х – дискретная случайная величина, которая в результате эксперимента принимала значения x₁, x₂,…, x_n с вероятностями p₁, p₂,…, p_n, 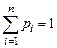. Тогда средним значением или математическим ожиданием величины X называется сумма 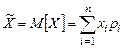, т.е. средневзвешенное значение величины Х, где весами служат вероятности p_i.

Пример. Определить среднее значение ошибки регулирования e, если на основании большого числа опытов установлено, что вероятность ошибки р_i равна:

Решение:

1. M[e] = 0,1×0,2 + 0,15×0,2 + 0,2×0,3 + 0,25×0,15 + 0,3×0,15 =

= 0,19 %.

В том случае, если g(Х) является функцией X (причем вероятность того, что X = x_i равна p_i), то среднее значение функции определяется как

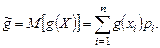
Предположим, что X – случайная величина с непрерывным распределением и характеризуется плотностью вероятности j(x). Тогда вероятность того, что X заключена между x и x + Dх:

.

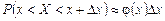Величина X при этом приближенно принимает значение x. В пределе при Dx ® 0, можно предположить, что приращение Dx численно равно дифференциалу dx.

Произведя замену Dx = dх, получаем точную формулу для расчета среднего значения Х :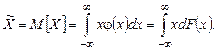

Аналогично для g(Х):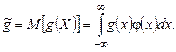

Как правило, недостаточно бывает знать только среднее значение (математическое ожидание) случайной величины. Для оценки меры случайности величины (для оценки разброса конкретных значений X относительно математического ожидания M[X]) вводится понятие дисперсии случайной величины. Дисперсия – среднее значение квадрата отклонения каждого конкретного значения X от математического ожидания. Чем больше дисперсия 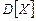, тем больше случайности разброса величины от математического ожидания. Если случайная величина дискретная, то

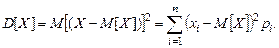
Для непрерывной случайной величины дисперсию можно записать аналогично:

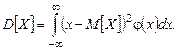
Дисперсия 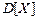хорошо описывает разброс величины, но при этом есть один недостаток: размерность 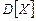не соответствует размерности X. Чтобы избавиться от этого недостатка, часто в конкретных приложениях рассматривают не 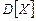, а положительное значение 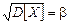, которое называется средним квадратическим отклонением.

1.3.2.1. Свойства математического ожидания

1. Математическое ожидание неслучайной величины равно самой этой величине M[C] = C.

2. Неслучайный множитель С можно выносить за знак математического ожидания M[CX] = CM[X].

3. Математическое ожидание суммы случайных величин равно сумме математических ожиданий этих случайных величин.

.

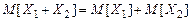4. Математическое ожидание произведения независимых случайных величин равно произведению математических ожиданий этих величин (условие независимости случайных величин).

.

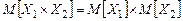1.3.2.2. Свойства дисперсии

1. Дисперсия неслучайной величины С равна нулю: D[C]=0.

2. Дисперсия произведения неслучайного множителя С на случайную величину равна произведению С² на дисперсию случайной величины.

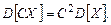
3. Дисперсия суммы независимых случайных величин X₁ и X₂ равна сумме дисперсий слагаемых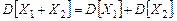

1.3.3. Моменты случайной величины

Пусть Х – непрерывная случайная величина. Если n – целое положительное число, а функция xⁿ интегрируема на интервале (–¥; +¥), то среднее значение

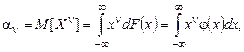n = 0, 1,…, n

называется начальным моментом порядка n случайной величины X.

Очевидно, что момент нулевого порядка

,

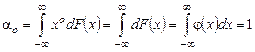а начальный момент первого порядка

,

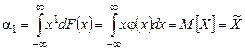есть математическое ожидание самой случайной величины Х.

Момент второго порядка

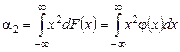
есть математическое ожидание квадрата случайной величины Х.

Аналогично находят a₂, a₃ и т.д.

Если 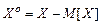– центрированная случайная величина, то представляет интерес рассмотрение центральных моментов порядка n, где n = 0, 1,…, n:

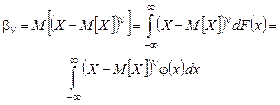
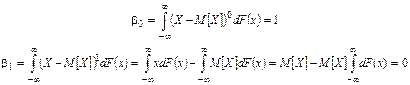
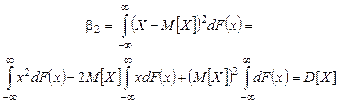
Есть связь между начальными и центральными моментами.

Так b_о = a_о

b₂=a₂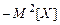

b₃=a₃ 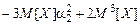и т.п.