Среднее и дисперсия выборки

Пусть М[Х] – математическое ожидание случайной величины Х. Это число нам неизвестно. Мы проводим наблюдения и при большом объеме выборки n можно вместо М[Х] рассматривать математическое ожидание Х_n. Погрешность при этом будет тем меньше, чем больше объем выборки n.

Математическое ожидание выборки есть просто среднее арифметическое элементов выборки:

.

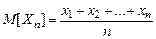Будем называть средним выборки 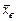. Если сгруппировать итоги наблюдений, то можно записать

,

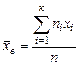где х_i – варианта выборки; n_i – частота варианты х_i; n – объем выборки.

Таким образом, в качестве истинного результата можно брать 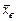. Такой выбор вносит определенные погрешности, которые тем меньше, чем больше n.

Дисперсия D[Х] приближенно равна дисперсии D[X_n].

,

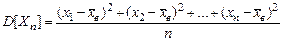т.е. D[Х] » D[X_n]. Это равенство было бы еще более надежным, если бы в формуле для D[X_n] вместо 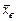стоял непосредственно истинный результат М[Х]. Обычно получаем заниженную оценку рассеяния значения генеральной совокупности. В связи с этим D[X_n] называется смещенной оценкой дисперсии D[X]. Чтобы получить несмещенную оценку дисперсии требуется рассмотреть величину

,

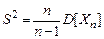которая является несмещенной оценкой дисперсии.

Переход к несмещенной оценке S² важен в основном для малых выборок, ибо разница между S² и D[X_n] при больших n незаметна.

Таким образом, среднее выборки

,

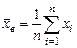а несмещенная оценка дисперсии выборки

.

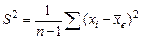В практических вычислениях для дисперсии S² часто удобна формула

.

Величина S (корень квадратный из выборочной дисперсии) называется средним квадратическим отклонением выборки или выборочным стандартом.

Почему в формуле дисперсии n заменили на n – 1? Это связано с тем, что входящая в формулу величина 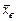сама зависит от элементов выборки. Если бы в формуле еще одна величина была функцией элементов выборки, то пришлось бы взять n – 2 и т.д.

Каждая величина, зависящая от элементов выборки и участвующая в формуле выборочной дисперсии, называется связью. Эта разность показывает, какое количество элементов выборки можно произвольно изменять, не нарушая связей и называется числом степеней свободы. Таким образом, знаменатель выборочной дисперсии всегда равен разности между объемом выборки и числом связей, наложенных на эту выборку.

2.2. Связь между случайными величинами. Корреляция

До сих пор изучали наблюдения над одной случайной величиной. Между тем для выяснения тех или иных причинно–следственных связей в окружающей природе необходимо вести одновременные наблюдения над целым рядом случайных величин, чтобы по полученным данным изучать взаимоотношения этих величин. Ограничимся пока двумя случайными величинами Х и У.

В математическом анализе зависимость между двумя величинами выражается понятием функции у = f(x), где каждому допустимому значению одной переменной соответствует одно и только одно значение другой переменной. Такая зависимость называется функциональной, она обнаруживается с помощью строгих логических доказательств и не нуждается в опытной проверке. Если у = const при изменении х, то говорят, что у не зависит от х.

Гораздо сложнее обстоит дело с понятием зависимости случайных величин: если при изменении х изменилось у, мы не можем сказать, является ли это изменение результатом зависимости у от х или это результат влияния случайных факторов. Здесь имеет место связь особого рода, при которой с изменением одной величины меняется распределение другой – такая связь называется стохастической.

Выявление стохастической связи и оценка ее силы представляют задачу математической статистики.

Рассматривая свойства дисперсии, мы указали, что дисперсия суммы двух независимых величин равна сумме дисперсий этих величин. Поэтому если для двух случайных величин Х и У окажется, что

,

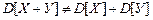то это служит верным признаком наличия зависимости между Х и У, т.е. корреляции.

Из этого неравенства вытекает (доказано), что справедливо следующее неравенство:

,

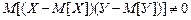где 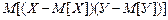называют корреляционным моментом.

Корреляционный момент зависит от единиц измерения величин Х и У. Поэтому на практике чаще используется безразмерная величина, которая называется коэффициентом корреляции.

.

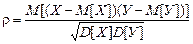2.2.1. Свойства коэффициента корреляции

1. Коэффициент корреляции независимых или некоррелированных величин равен нулю.

2. Коэффициент корреляции не меняется от прибавления к Х или У каких–либо постоянных (неслучайных) слагаемых, от умножения их на положительные числа.

3. Если одну из случайных величин, не меняя другой, умножить на 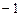, то на 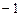умножится и коэффициент корреляции.

4. Численно коэффициент корреляции заключен в пределах 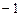£ r £ 1. Если коэффициент корреляции отличен от нуля, то он своей величиной характеризует не только наличие, но и силу стохастической связи между Х и У. Чем больше абсолютная величина r, тем сильней корреляция между Х и У. Максимальная корреляция соответствует |r|=1. Это возможно, когда между случайными величинами существует строгая функциональная связь.

5. Если r > 0, то величины Х и У с точностью до случайных погрешностей одновременно возрастают или убывают, если же r < 0, то с возрастанием одной величины другая убывает.

Но это справедливо только для линейной зависимости У от Х. Т.е. зависимость между Х и У может быть строго функциональной (например, квадратичной) без следа случайности, а коэффициент корреляции все еще будет меньше 1. Таким образом, коэффициент корреляции есть показатель того, насколько связь между случайными величинами близка к строгой линейной зависимости. Он одинаково отмечает и слишком большую долю случайности, и слишком большую криволинейность этой связи.

Если заранее, из общих соображений, можно предсказать линейную зависимость, то r является достаточным показателем тесноты связи между Х и У.

Для случайных величин (большинство именно таких), подчиняющихся нормальному закону, равенство r = 0 означает одновременно и отсутствие всякой зависимости.