Доверительных областей для параметров
3.1. Доверительные интервалы и доверительные вероятности
Выборочные параметры могут служить приближенными оценками соответствующих генеральных параметров. Погрешность такой оценки, как об этом говорилось ранее, тем меньше, чем больше объем выборки. Как можно оценить эту погрешность более строго?
Все выборочные параметры ( 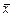 , S2) являются случайными величинами и их отклонения от генеральных параметров (погрешности) также будут случайными. Поэтому вопрос об оценке этих отклонений носит вероятностный характер и можно лишь указать вероятность той или иной погрешности, т.е. найти вероятность того, что некоторая случайная величина Dn (отклонение выборочного параметра n от исследуемого генерального) не превосходит по абсолютной величине некоторого заданного числа e. Задача легко решается, если известны функции распределения F(x) или j(х) величины Dn.
, S2) являются случайными величинами и их отклонения от генеральных параметров (погрешности) также будут случайными. Поэтому вопрос об оценке этих отклонений носит вероятностный характер и можно лишь указать вероятность той или иной погрешности, т.е. найти вероятность того, что некоторая случайная величина Dn (отклонение выборочного параметра n от исследуемого генерального) не превосходит по абсолютной величине некоторого заданного числа e. Задача легко решается, если известны функции распределения F(x) или j(х) величины Dn.
Известно:
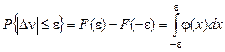 .
.
Но, к сожалению, обычно и F(x), и j(х) неизвестны.
Задачу решают по другому. Находят с заданной вероятностью границы возможных значений изучаемого параметра. Эту заданную вероятность называют доверительной вероятностью. В зависимости от конкретных обстоятельств в качестве доверительной вероятности берут р = 0,95; 0,98; 0,99; реже р = 0,90 или р = 0,999.
Иногда вместо доверительной вероятности рассматривают связанную с ней величину – так называемый уровень значимости a=1 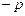 .
.
Соответствующие доверительной вероятности границы значений параметра называют доверительными границами, а образуемый ими интервал – доверительным интервалом.
Представляет интерес оценка генерального среднего и генеральной дисперсии с точки зрения определения их доверительных границ.
3.2. Оценка генерального среднего
Предполагается, что наблюдаемая случайная величина имеет нормальное распределение. Для оценки генерального среднего желательно знать генеральную дисперсию s2. Но ее нельзя найти из наблюдений и вместо нее обычно берут выборочную дисперсию S2.
Вводят величину
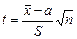 ,
,
где 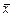 – выборочное среднее; S2 – выборочная дисперсия; а – генеральное среднее; n – объем выборки.
– выборочное среднее; S2 – выборочная дисперсия; а – генеральное среднее; n – объем выборки.
Таким образом, величина t – это не что иное, как нормированное отклонение 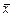 от а.
от а.
Функция распределения величины t называется t –распределением, или распределением Стьюдента. Она зависит только от числа f степеней свободы, по которым подсчитана дисперсия S2. Если дисперсия S2 и среднее 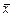 подсчитывались по одним и тем же наблюдениям, то f = n - 1. Плотность j(t) распределения Стьюдента имеет вид:
подсчитывались по одним и тем же наблюдениям, то f = n - 1. Плотность j(t) распределения Стьюдента имеет вид:
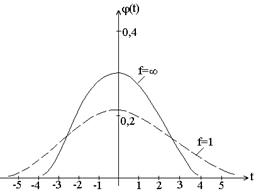
По форме графики напоминают плотность нормального распределения, но при t ® ±¥ они значительно медленнее сближаются с осью абсцисс.
Представляет интерес рассмотрение одной из числовых характеристик случайной величины, которую называют квантиль.
Квантилем хр случайной величины Х с функцией распределения F(x) называют решение уравнения
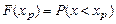 ,
,
где вероятность Р – заданная величина (см. кривую распределения).
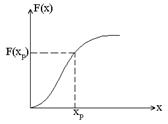
Величины квантилей представлены в специальных таблицах для соответствующих значений вероятности Р.
Возвращаясь к распределению Стьюдента, обозначим tp – квантиль t–распределения.
Если 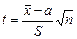 , то известно, что доверительные границы генерального среднего могут быть определены из двусторонних неравенств
, то известно, что доверительные границы генерального среднего могут быть определены из двусторонних неравенств
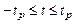 или
или 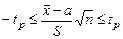 .
.
Преобразуем поэтапно двустороннее неравенство. Для этого:
1) Берем левую границу:
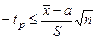 ;
; 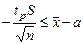 ;
;
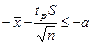 ; откуда
; откуда 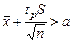 .
.
2) Рассматриваем правую границу:
 ;
;  ;
;
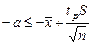 ; или, в итоге
; или, в итоге 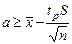 .
.
Окончательно получаем:
 ,
,
что можно представить в виде:
 .
.
Таким образом, с вероятностью р – генеральное значение математического ожидания заключается в границах между 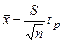 и
и 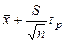 , где величина tр определяется по таблицам распределения Стьюдента для заданной доверительной вероятности р и определяемого числа степеней свободы f = n
, где величина tр определяется по таблицам распределения Стьюдента для заданной доверительной вероятности р и определяемого числа степеней свободы f = n 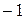 .
.
Распределение Стьюдента позволяет оценивать генеральное среднее (математическое ожидание), когда генеральная дисперсия неизвестна. При этом число наблюдений может быть очень малым, даже равным двум. Конечно, скудость информации сказывается на результатах – доверительные границы получаются довольно широкими. Поэтому везде, где это только возможно, нужно стараться увеличивать число степеней свободы у выборочной дисперсии.
Пример. Выборочное среднее 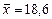 найдено по трем наблюдениям, а выборочная дисперсия определена как S2 = 0,25, при этом f = 3 - 1 = 2. В качестве доверительной вероятности возьмем р = 0,95, Величину tp найдем из таблицы Стьюдента, где для f = 2 и р = 0,95 находим tp = 4,30.
найдено по трем наблюдениям, а выборочная дисперсия определена как S2 = 0,25, при этом f = 3 - 1 = 2. В качестве доверительной вероятности возьмем р = 0,95, Величину tp найдем из таблицы Стьюдента, где для f = 2 и р = 0,95 находим tp = 4,30.
Тогда учитывая, что 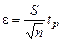 , доверительная оценка определится как:
, доверительная оценка определится как:
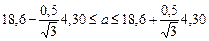 .
.
После вычислений получаем окончательные значения доверительной оценки генерального среднего
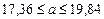 .
.
В некоторых задачах требуется найти одностороннюю доверительную оценку генерального среднего, т.е. оценку только сверху или только снизу. При этом задача решается аналогично.
3.3. Оценка генеральной дисперсии
Для оценки генеральной дисперсии s2 используется выборочная дисперсия S2. Эта дисперсия в силу случайности выборки сама является случайной величиной. Но математическим ожиданием для S2 служит генеральная дисперсия s2. Отсюда следует, что s2 можно оценить по S2, если известно распределение величины S2.
Распределение величины S2 можно получить с помощью так называемого распределения Пирсона (или c2 – распределения). Для выборки с элементами х1, х2,…,хn через c2 обозначается сумма
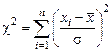 .
.
В этой сумме есть связь 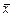 , поэтому число степеней свободы f = n -1. Плотность c2 – распределения зависит только от f, соответствующие графики приведены на рисунке.
, поэтому число степеней свободы f = n -1. Плотность c2 – распределения зависит только от f, соответствующие графики приведены на рисунке.
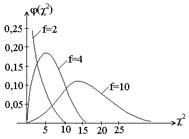
Нетрудно установить связь между величинами c2 и S2:

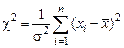 или
или 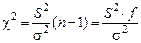 .
.
Теоретически доказано и подтверждено практикой, что для уровня значимости a = 1 - р доверительная оценка величины c2 имеет вид
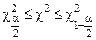 ,
,
где 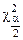 и
и 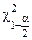 – соответствующие квантили распределения Пирсона.
– соответствующие квантили распределения Пирсона.
Отсюда
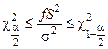
или после преобразований
 .
.
Таким образом получили двустороннюю доверительную оценку для генеральной дисперсии s2.
3.4. Проверка статистических гипотез применяется для того, чтобы использовать полученную по выборке информацию для суждения о законе распределения генеральной совокупности. При этом имеется определенное представление о неизвестном вероятностном законе F(x) и его параметрах, которое формулируется в виде статистической гипотезы, обозначаемой символом Но (нулевая, или основная гипотеза).
Запись 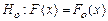 означает допущение («гипотезу») о том, что Fo(x) есть функция распределения генеральной совокупности.
означает допущение («гипотезу») о том, что Fo(x) есть функция распределения генеральной совокупности.
С помощью статистических методов или критериев для проверки гипотезы устанавливается, соответствуют ли взятые из выборки данные выдвинутой гипотезе или нет, т.е. нужно ли принять или отвергнуть гипотезу.
Если вид функции распределения F(x) задан отдельными параметрами и если гипотеза строится именно по этим неизвестным параметрам, то говорят о параметрических гипотезах.
Для проверки гипотезы вводят критерий – правило, позволяющее принять или отвергнуть гипотезу в соответствии с данными эксперимента.
Особое положение занимает проверка адекватности модели регрессии.
Адекватная модель регрессии, как правило, неизвестна. Подбирая, например, параболическую модель мы не знаем заранее, какого она должна быть порядка, на какой степени следует остановиться. Не знаем мы также, сколько факторов надо учитывать. Поэтому обычно начинают с моделей первого порядка – линейных моделей и затем повышают порядок модели (степень многочлена) до тех пор, пока при сравнительно небольшом числе параметров модель не станет адекватной, т.е. гипотеза об ее истинности не будет противоречить данным эксперимента (если это вообще возможно, если существует такая параболическая модель). Для проверки адекватности модели обычно используют критерий Фишера.
3.4.1. Гипотеза о равенстве дисперсий. Критерий Фишера
Сравнение двух или нескольких выборочных дисперсий является одной из важнейших задач статистической обработки наблюдений. Основной выясняемый вопрос при этом – можно ли считать сравниваемые выборочные дисперсии оценками одной и той же генеральной дисперсии.
Начнем со сравнения двух выборочных дисперсий 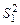 и
и 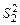 , имеющих соответственно f1 и f2 степеней свободы. Будем считать, что первая выборка сделана из генеральной совокупности с дисперсией
, имеющих соответственно f1 и f2 степеней свободы. Будем считать, что первая выборка сделана из генеральной совокупности с дисперсией 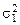 , вторая – из генеральной совокупности с дисперсией
, вторая – из генеральной совокупности с дисперсией 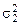 . Выдвигается нулевая гипотеза – гипотеза о равенстве генеральных дисперсий
. Выдвигается нулевая гипотеза – гипотеза о равенстве генеральных дисперсий 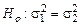 . Для того, чтобы отвергнуть эту гипотезу, нужно доказать значимость расхождения между
. Для того, чтобы отвергнуть эту гипотезу, нужно доказать значимость расхождения между 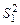 и
и 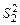 при выбранном уровне значимости a =
при выбранном уровне значимости a = 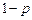 . В качестве критерия значимости обычно используется так называемое распределение Фишера.
. В качестве критерия значимости обычно используется так называемое распределение Фишера.
Распределением Фишера (или F–распределением) называется распределение случайной величины:
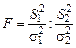 .
.
Это распределение зависит только от f1 и f2 при этом
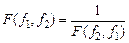 .
.
|
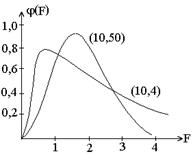
На рисунке приведены графики плотности F–распределения при сочетаниях (f1, f2) = (10,4) и (10,50).
Как и в случае c2–распределения, плотность рассматривается лишь на положительной полуоси, т.е. при 0 £ F £ ¥. В литературе даются квантили F1–р для некоторых наиболее употребительных уровней значимости a = 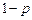 и различных комбинаций f1 и f2. При нахождении квантилей Fр для значений р, не вошедших в таблицу, используется очевидное соотношение
и различных комбинаций f1 и f2. При нахождении квантилей Fр для значений р, не вошедших в таблицу, используется очевидное соотношение
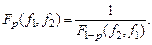
Например: F0,95(4,3) = 9,1; F0,05(3,4) = 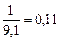 .
.
Вернемся к рассмотрению нулевой гипотезы, согласно которой 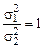 . В этом случае
. В этом случае 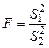 и, следовательно, F–распределение может быть использовано непосредственно для оценки отношения
и, следовательно, F–распределение может быть использовано непосредственно для оценки отношения 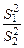 . При этом должно выполняться двустороннее неравенство
. При этом должно выполняться двустороннее неравенство
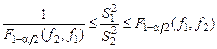 . (*)
. (*)
При этом будем обозначать через 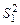 , большую из сравниваемых дисперсий. Если большей выборочной дисперсии заведомо не может соответствовать меньшая генеральная, т.е. если неравенство
, большую из сравниваемых дисперсий. Если большей выборочной дисперсии заведомо не может соответствовать меньшая генеральная, т.е. если неравенство 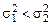 заведомо невозможно, то нужно применять односторонний критерий, сравнивая отношение
заведомо невозможно, то нужно применять односторонний критерий, сравнивая отношение 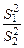 с односторонними доверительными оценками:
с односторонними доверительными оценками:
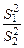 £ F1–a(f1, f2).
£ F1–a(f1, f2).
Нулевая гипотеза отвергается, если 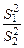 ³ F1–a(f1, f2), где значение F берется из таблицы для квантилей распределения Фишера.
³ F1–a(f1, f2), где значение F берется из таблицы для квантилей распределения Фишера.
Пример. При изучении стабильности температуры в термостате получены данные 21,2; 21,8; 21,3; 21,0; 21,4; 21,3. К стабилизатору температуры применено некоторое усовершенствование, после чего (на другом режиме) получены данные: 37,7; 37,6; 37,6; 37,4. Можно ли при уровне значимости a = 0,05 считать усовершенствование эффективным?
Эффективность стабилизаторов температуры, очевидно, зависит от даваемой ими дисперсии температур. Таким образом, задача состоит в том, чтобы сравнить генеральные дисперсии данных выборок температур. Вычисляем выборочные дисперсии, уменьшив для удобства вычислений все данные на 21 в первом случае и на 37,5 – во втором:
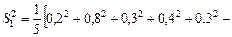
 ,
,
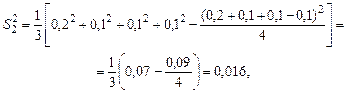
Отсюда  .
.
Числа степеней свободы f1 = 5, f2 = 3.
Усовершенствование может лишь уменьшить дисперсию, поэтому применяем односторонний критерий значимости. По таблице квантилей распределения Фишера находим F0,95(5,3) = 9,0. Мы видим, что 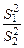 = 4,4 < 9,0. Следовательно, данные наблюдений не позволяют отвергнуть нулевую гипотезу и считать усовершенствование эффективным. Таким образом, различие дисперсий незначимо.
= 4,4 < 9,0. Следовательно, данные наблюдений не позволяют отвергнуть нулевую гипотезу и считать усовершенствование эффективным. Таким образом, различие дисперсий незначимо.
3.5. Проверка адекватности уравнения регрессии
(математической модели)
После завершения вычислений, связанных с получением оценок коэффициентов регрессии, проверяется адекватность полученного уравнения.
Для проверки значимости (адекватности) уравнения регрессии в целом с использованием F–критерия Фишера общую дисперсию 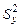 сравнивают с остаточной дисперсией
сравнивают с остаточной дисперсией  .
.
Общая дисперсия У:
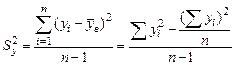 ,
,
где n – объем выборки; уi (i = 1, 2,…, n) – выборочные значения у.
Остаточная дисперсия (дисперсия неадекватности)
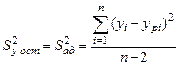 ,
,
т.е. показатель ошибки предсказания уравнением регрессии результатов опытов, где урi – расчетное значение величины у, вычисленное по полученному уравнению регрессии (двойка в знаменателе) – количество переменных в уравнении регрессии.
Качество предсказания определяют, сравнивая  с
с 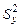 . Находят
. Находят 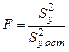 (делят всегда большую величину на меньшую).
(делят всегда большую величину на меньшую).
Для заданной величины уровня значимости 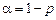 по таблице критерия Фишера (и для соответствующих значений степеней свободы f1 и f2) определяют табличное значение критерия Fтаб.
по таблице критерия Фишера (и для соответствующих значений степеней свободы f1 и f2) определяют табличное значение критерия Fтаб.
Для того, чтобы уравнение регрессии адекватно описывало результаты экспериментов с определенной доверительной вероятностью «р» требуется выполнение следующего условия: F < Fтаб.
Пример. Данные эксперимента
| № п/п | х | у |
| 1,5 | 5,0 | |
| 4,0 | 4,5 | |
| 5,0 | 7,0 | |
| 7,0 | 6,5 | |
| 8,5 | 9,5 | |
| 10,0 | 9,0 | |
| 11,0 | 11,0 | |
| 12,5 | 9,0 | |
| å | 59,5 | 61,5 |
Расчеты по известной методике позволяют получить для уравнения регрессии a = 3,73; b = 0,53, т.е. линейное уравнение регрессии имеет вид:
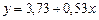 .
.
Оценим значимость этого уравнения с использованием критерия Фишера. Для этого определяем общую дисперсию у:
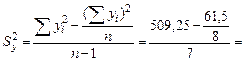
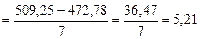
(при этом 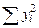 и
и 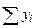 взяты из таблицы, по которой определяют коэффициенты регрессии).
взяты из таблицы, по которой определяют коэффициенты регрессии).
Остаточная дисперсия  и находится с помощью таблицы
и находится с помощью таблицы
| № п/п | yi | xi | ypi = 3,73 + 0,53xi | yi – ypi | (yi – ypi)2 |
| 5,0 | 1,5 | 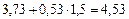
| +0,47 | 0,2209 | |
| 4,5 | 4,0 | 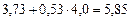
| –1,35 | 1,82225 | |
| 7,0 | 5,0 | 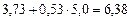
| +0,62 | 0,3844 | |
| 6,5 | 7,0 | 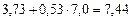
| –0,94 | 0,8836 | |
| 9,5 | 8,5 | 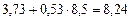
| +1,26 | 1,5876 | |
| 9,0 | 10,0 | 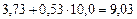
| –0,03 | 0,0009 | |
| 11,0 | 11,0 | 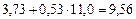
| +1,44 | 2,0736 | |
| 9,0 | 12,5 | 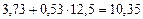
| –1,35 | 1,8225 | |
| å | 61,5 | 59,5 | 0,12 | 8,8 |
Откуда
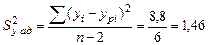 .
.
Определяем
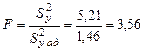 .
.
Для 5 % уровня значимости (a = 0,05) и для f1 = 7, a f2 = 6, Fтаб = 4,21
F < Fтаб, т.е. уравнение регрессии адекватно.
Дата добавления: 2016-03-27; просмотров: 1103;
