В системах управления

4.1. Случайные процессы

Функция, значение которой при каждом данном значении независимой переменной является случайной величиной, называется случайной функцией. То есть, это бесконечная совокупность случайных величин, зависящая от непрерывно изменяющейся независимой переменной. Случайная функция, зарегистрированная по результатам опыта, называется реализацией случайной функции. Случайная функция, для которой независимой переменной является время t называется случайным (стохастическим) процессом.

Для характеристики случайной функции служат моменты случайной функции. Для их определения необходимо знать многомерные функции распределения случайной величины.

Предположим, что мы располагаем большим числом однотипных систем, работающих одновременно при одинаковых условиях. Будем наблюдать изменения величин на выходе этих устройств. Они будут характеризоваться некоторыми случайными функциями 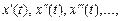причем все эти функции будут отличаться друг от друга.

Рассмотрим какой–либо момент времени t и найдем, какая доля из общего числа функций x(t) имеет в этот момент времени значение, заключенное между х и x + dx.

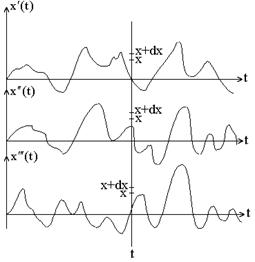
Эта доля зависит от момента времени t и пропорциональна dx при малых dx. Обозначим ее через w₁(х, t)dx – (при количестве реализаций, стремящихся к бесконечности, эта величина соответствует вероятности того, что в момент времени t величина х будет заключена в пределах х и х + dх) и назовем w₁(х, t) – первой или одномерной функцией распределения вероятности.

Рассмотрим теперь все возможные пары значений х, наблюденные в два различных момента времени t₁ и t₂. Долю пар значений х, для которой величина х заключена между (х₁, х₁+ dх₁) при t = t₁ и между (х₂, х₂ + dх₂) при t = t₂, отнесенную к общему числу наблюденных пар значений, обозначим через w₂(х₁, t₁, х₂, t₂)dx₁dx₂ и назовем второй или двумерной функцией распределения вероятности.

Этот процесс можно продолжить и определить третью, четвертую и все последующие функции распределения вероятности.

Итак, случайный процесс можно характеризовать некоторыми функциями распределения вероятности, полностью определяющими его в статистическом смысле.

Действительно, зная w₁(х, t) можно определить математическое ожидание m_ox(t) случайной величины х(t):

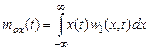
и его дисперсию b_2х(t):

.

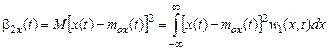Зная вторую функцию распределения w₂(х₁,t₁, х₂,t₂), можно определить как m_ox(t), b_2х(t), так и центральный момент 2–го порядка:

,

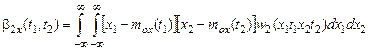характеризующий связь между значениями случайной функции в различные моменты времени. Функция b_2х(t₁,t₂) называется корреляционной функцией.

Зная n–мерную функцию распределения вероятности, можно определить все последующие моменты случайной функции, включая момент n–го порядка.

Если приходится иметь дело не с одной, а с несколькими взаимосвязанными функциями, то кроме их собственных моментов, приходится вводить еще и их взаимные моменты.

Так, например, если имеются две случайные функции х(t) и y(t), то простейшим взаимным моментом является момент 2–го порядка:

=

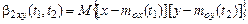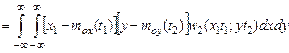
называемый взаимной корреляционной функцией случайных процессов х(t) и y(t).

4.2. Стационарные случайные процессы

Общая теория случайных функций, требующая задания многомерных функций распределения вероятности, обычно оказывается очень сложной и громоздкой для практических применений.

Но, если случайные функции имеют нормальное распределение, то задание их первых двух моментов достаточно для определения всех последующих моментов, вследствие чего корреляционная теория (2–ой центральный момент – корреляционный момент) может рассматриваться как общая теория случайных функций с нормальным распределением.

Но и корреляционная теория достаточно сложна, поэтому обычно рассматривают те или иные виды случайных процессов, удовлетворяющих определенным допущениям.

Особое место занимают стационарные случайные процессы. Для них вид функции распределения вероятности не зависит от смещения начала отсчета вдоль оси времени. В случае стационарных случайных процессов определение функции распределения упрощается в том отношении, что она может быть определена в течение достаточно долгого промежутка времени из результатов наблюдения над одной единственной системой, а не над многими. Действительно, так как в этом случае функция распределения не зависит от начала отсчета времени, то можно предположить, что экспериментальную запись кривой х(t), полученную из наблюдения над одной системой в течение достаточно долгого промежутка времени, можно разбить на ряд отрезков длиной Т (где Т велико по сравнению со всеми «периодами», которые имеются в исследуемом процессе) и считать, что функциями, входящими в совокупность, являются функции х(t), представляющие собой части всей кривой х(t) на протяжении каждого из отрезков Т.

В основе этого предположения лежит так называемая эргодическая гипотеза, согласно которой большое число наблюдений над одной – единственной системой, движение которой представляет собой стационарный случайный процесс, в моменты времени, выбранные произвольным образом, имеет те же статистические свойства, то же число наблюдений над произвольно выбранными подобными ей системами в один и тот же момент времени.

Различают «среднее значение по совокупности (множеству)», т.е. средние значения, определенные на основании наблюдения над многими подобными системами в один и тот же момент времени, и «среднее по времени», т.е. среднее значение, определенное на основании наблюдения над одной из этих систем для достаточно большого числа последующих моментов времени.

Для стационарных процессов это одно и то же. Так, например, для функции х(t) «среднее по совокупности» :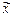

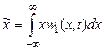– зависит от момента времени t, а среднее по времени 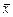для интервала времени 2Т:

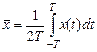– не зависит от t и для стационарного процесса = .

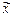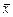Аналогичное равенство имеет место и для моментов более высокого порядка.

4.3. Корреляционная функция

Важной вероятностной характеристикой случайного процесса является корреляционная функция, которая для стационарного случайного процесса х(t) определится как:

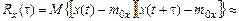
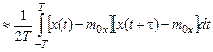
где 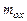= 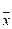– математическое ожидание («среднее по времени» на интервале Т).

Для «центрированного» случайного процесса 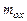= 0 и

.

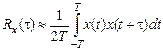Корреляционную функцию случайного процесса х(t) называют еще автокорреляционной функциейR_x(t), так как если приходится иметь дело с двумя стационарными случайными процессами х(t) и у(t), то кроме их математических ожиданий 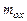, 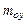и автокорреляционных функций R_x(t) и R_y(t), обычно вводится в рассмотрение корреляционная функция связи, или взаимная корреляционная функция, которая для стационарного случайного процесса –

.

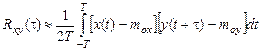Если 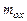= =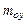0, то

.

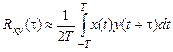Она имеет непосредственную связь с понятием коэффициента корреляции. Так, если коэффициент корреляции характеризует меру зависимости между двумя системами чисел х_i и y_i (случайные величины), то взаимная корреляционная функция характеризует зависимость значений одной и той же или различных случайных функций в различные моменты времени.

4.3.1. Свойства корреляционной функции

Для простоты предположим, что m_ох = 0.

1. Начальное значение корреляционной функции R(t) равно среднему значению квадрата случайной функции и поэтому существенно положительно, т.е.

.

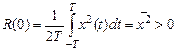2. Корреляционная функция есть четная функция t, т.е.

.

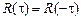Действительно,

.

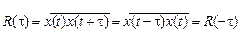3. Значение R(t) при любом t не может превышать ее начального значения R(0), т.е.

.

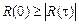4. Корреляционная функция R(t) для достаточно больших t стремится к нулю, т.е.

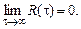
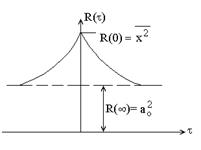
5. Если х(t) представляет собой, например, стационарный случайный процесс с наложенной на него постоянной составляющей а_о, то R(t) будет иметь вид, изображенный на рисунке:

При этом ее начальная ордината R(0) равна среднему значению квадрата сигнала х(t), а ее конечная ордината R(¥) – значению квадрата постоянной составляющей сигнала х(t), т.е. величине .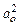

6. Если х(t) представляет собой стационарный случайный процесс с наложенной на него периодической составляющей, то R(t) также будет содержать периодическую составляющую с тем же периодом и, следовательно, будет иметь вид:

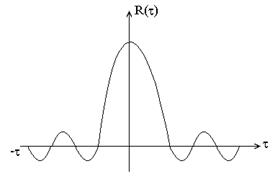
7. «Белый шум». Случайный процесс х(t), который характеризуется тем, что в нем отсутствует какая–либо взаимная связь между предыдущим и последующим значениями х(t), называется абсолютно случайным процессом или «белым шумом». Очевидно, что в этом случае корреляционная функция равна нулю при всех значениях t, кроме t = 0, и ее можно представить в виде d–функции или практически в виде импульса достаточно большой амплитуды, но малой ширины, площадь которого равна единице.

Взаимная корреляционная функция R_xy(t) не является четной, в отличие от R_х(t), но для нее справедливо равенство: R_xy(t)=R_yх( 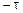). Кроме того: .

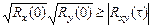4.4. Спектральная плотность

Спектральная плотность случайного процесса х(t) определяется как преобразование Фурье от корреляционной функции R_x(t):

.

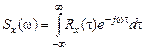Это так называемая автоспектральная плотность. В свою очередь в соответствии с формулой обратного преобразования Фурье:

.

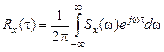S_x(w) играет большую роль при исследовании преобразования случайных сигналов линейными системами.

Автоспектральная плотность S_x(w) – действительная и четная функция.

Так, используя формулу Эйлера, можно записать:

.

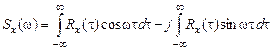Но R_x(t) – четная функция, т.е. R_x(t) = R_x( 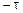), а 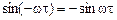, поэтому во втором слагаемом подынтегральное выражение представляет собой нечетную функцию переменного t.

Поэтому .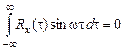

И тогда 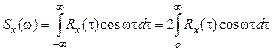, и следовательно

.

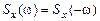Аналогично

.

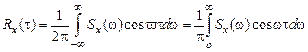Эти соотношения позволяют определить S_x(w) по заданной аналитически или в виде графика R_x(t), или наоборот. В любом случае для определения функции S(w) по R(t) и наоборот можно использовать таблицы преобразования Фурье.

4.4.1. Свойства спектральной плотности

1. Если R(t) – монотонно убывающая функция t, то S(w) – также монотонно убывающая функция w.

2. Чем уже функция R(t), тем более пологой и широкой является функция S(w).

3. Если R(t) стремится к нулю в течение очень короткого времени D, то S(w) сохраняет постоянное значение до частоты порядка .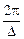

4. Спектральная плотность "белого шума" равна интегралу от d–функции, т.е. равна единице. Таким образом, энергия "белого шума" распределена по спектру равномерно и его суммарная энергия равна бесконечности, что физически нереализуемо.

5. Если случайная функция содержит постоянную составляющую, то в кривой спектральной плотности в точке w = 0 имеется d–функция (практически – острый импульс).

6. Если случайная функция имеет периодическую составляющую частоты w_о, то в составе кривой S(w) имеется две d–функции в точках ±w_о.