Примеры законов распределения случайной величины

Рассмотрим примеры распределения случайной величины.

1.4.1. Равномерное распределение дискретной случайной

величины

При бросании игральной кости может выпасть 1,2,3,… или 6. Здесь величина Х принимает значения х_i = i с вероятностями соответственно 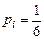(i = 1, 2, 3…, 6). Ввиду равенства всех вероятностей можно говорить о равномерном распределении случайной величины Х.

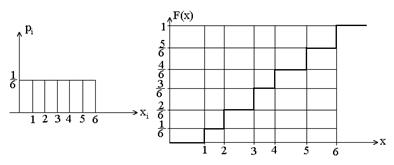
Рассчитаем для этой случайной величины математическое ожидание М[X] и дисперсию D[X]:

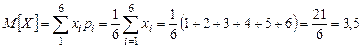
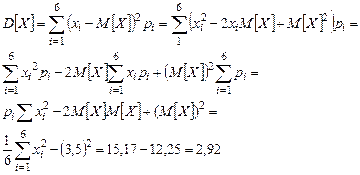
При этом .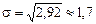

1.4.2. Равномерное распределение непрерывной случайной

величины

Предположим, что случайная величина имеет равномерное и непрерывное распределение. Причем ее плотность вероятности 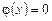для всех значений, кроме интервала (a, b), на котором она постоянна. Постоянное значение обозначим через A. Тогда можно записать

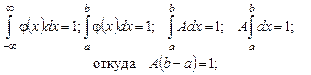
или 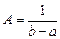. Поэтому плотность равномерного распределения задается формулой

.

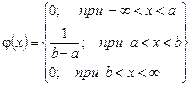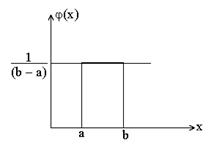
Случайная величина называется непрерывной, если ее функция распределения F(x) непрерывна на всей числовой оси, а плотность вероятности j(x) существует и непрерывна всюду, кроме дискретного множества точек. Для нахождения функции распределения F(x) воспользуемся формулой

.

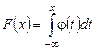При x £ a 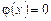. Тогда F(x) = 0.

Для а < x < b получим

.

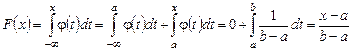Наконец при х ³ b получим:

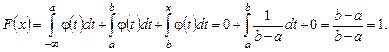
Таким образом интегральный закон равномерного распределения случайной величины задается формулой

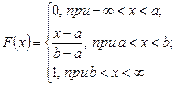
и соответственно в виде графика:

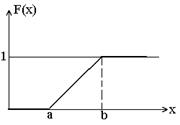
Числовые характеристики непрерывной случайной величины

.

;

;

; .

.

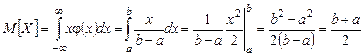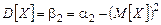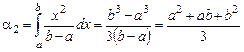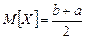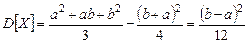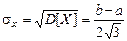1.4.3. Нормальный закон распределения (закон Гаусса)

Среди законов распределения, которым подчиняются встречающиеся на практике случайные величины, чаще всего приходиться иметь дело с нормальным законом распределения. Это предельный закон, к которому приближаются многие другие законы распределения при определенных условиях. Если случайную величину можно рассматривать как результат суммарного воздействия многих независимых факторов, то закон распределения такой случайной величины будет близок к нормальному.

Для этого закона плотность вероятности задается формулой:

.

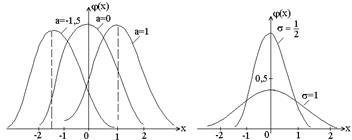
Выясним геометрический смысл параметров «а» и «s» (а – математическое ожидание; s² – дисперсия, s – среднеквадратическое отклонение).

Из формулы видно, что кривая у = j(х) достигает максимума при х = а, причем максимальное значение 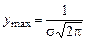. С ростом s величина максимального значения уменьшается, а так как площадь, ограниченная всей кривой и осью абсцисс, равна единице, то с ростом s кривая как бы растягивается вдоль оси ох и наоборот. Приведены графики у = j(х) при различных «а», но при одном и том же s. На другом – при а = 0, но различных s.

При 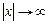имеет место предел, когда j = 0 ( по формуле). Разность (х 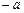) содержится в формуле в квадрате, т.е. график функции симметричен относительно прямой х = а.