Определение коэффициента корреляции по данным
Наблюдений
Допустим, что проведено n испытаний и при каждом отмечались значения двух случайных величин. В результате получается n пар выборочных значений (х1, у1), (х2, у2),…, (хn, уn). Для наглядности эти пары значений можно рассматривать как координаты точек на плоскости. Образовавшаяся совокупность точек сразу же дает представление о силе корреляции, где
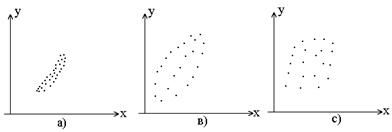
а - сильная корреляция; в - слабая корреляция; с - отсутствие корреляции
Выборочный коэффициент корреляции r вычисляется по той же формуле, что и генеральный коэффициент r, только здесь берутся выборочные математические ожидания (средние) и дисперсии. Если через 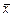 и
и 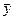 обозначить средние значения для хi и yi:
обозначить средние значения для хi и yi:
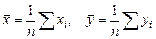 ,
,
то выборочный корреляционный момент равен
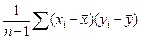 ,
,
откуда
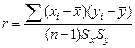 ,
,
где через 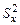 и
и 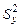 обозначены выборочные дисперсии
обозначены выборочные дисперсии
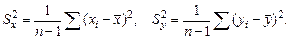
Удобнее при вычислениях пользоваться следующими выражениями:
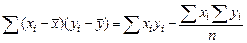 ,
,

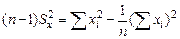 ,
,

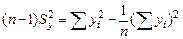 .
.
 При достаточно большом объеме выборки n выборочный коэффициент корреляции r приближенно равен генеральному коэффициенту r. Однако оценить возникающую при этом погрешность очень трудно. Это и не обязательно, так как точное значение r в расчетах почти не используется и нужно нам лишь как показатель силы связи.
При достаточно большом объеме выборки n выборочный коэффициент корреляции r приближенно равен генеральному коэффициенту r. Однако оценить возникающую при этом погрешность очень трудно. Это и не обязательно, так как точное значение r в расчетах почти не используется и нужно нам лишь как показатель силы связи.
В связи со случайностью выборки выборочный коэффициент корреляции r может быть отличен от нуля, даже если между наблюдаемыми величинами нет корреляции. Следовательно, для проверки гипотезы об отсутствии корреляции необходимо проверять, значительно ли r отличается от нуля.
2.2.3. Частная линейная корреляция
Одним из методов исследования линейной связи между тремя ( или несколькими) признаками, измеряемыми единовременно у некоторых элементов, является линейная корреляция, применяемая в случае равнозначности признаков, когда неудобно делить их на независимые и зависимые случайные переменные (как это было сказано раньше). При этом различают частную линейную и множественную линейную корреляции.
Обозначим эти признаки Х, У, Z.
Например: исследуют свойства некоторого сорта стали: Х – предел текучести, У – предел прочности, Z – предел упругости.
Рассматривая каждый раз только по два из трех признаков, можно в качестве меры линейной зависимости вычислить эмпирические простые коэффициенты корреляции rху, rxz, rуz (аналогично расчетам, соответствующим парной корреляции). При рассмотрении более двух признаков, однако, для получения безупречного статистического решения простых коэффициентов корреляции оказывается уже недостаточно. Так, rxz выражает зависимость между Х и Z. Но она может возникнуть и по той причине, что оба признака в большей или меньшей мере подвержены воздействию третьего признака – У.
Чтобы исключить влияние третьей случайной величины на две другие, вводят эмпирические частные коэффициенты корреляции, обозначенные через 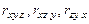 .
.
Буквы перед точкой указывают, между какими признаками изучается зависимость, а буква после точки – влияние какого признака исключается. Разумеется 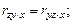
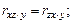
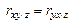 .
.
Принятые обозначения легко распространить на частные коэффициенты корреляции для числа признаков больше трех и выражать линейную связь только между двумя признаками, исключая каждый раз воздействие остальных.
Частные коэффициенты корреляции рассчитываются по простым коэффициентам корреляции согласно формулам
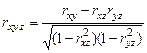 ,
,
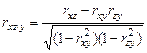 ,
,
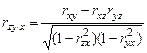 .
.
Второе и третье уравнения выводятся из первого путем циклической перестановки букв х, у, z. Подобно простым коэффициентам корреляции частные коэффициенты могут принимать значения, заключенные между –1 и +1.
Частные коэффициенты корреляции в большей или меньшей степени отклоняются от простых коэффициентов корреляции в зависимости от того, какое воздействие третий, исключаемый, признак оказывает на два оставшихся.
2.2.4. Множественная линейная корреляция
Для ответа на вопрос, зависит ли один из признаков одновременно от двух других (или у от х1 и х2 при взаимном влиянии х1 и х2), вводятся эмпирические множественные коэффициенты корреляции 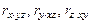 . Они являются мерой линейной связи между одним из признаков (буква индекса перед точкой) и совокупностью других признаков. Эти коэффициенты заключены в переделах –1 и +1.
. Они являются мерой линейной связи между одним из признаков (буква индекса перед точкой) и совокупностью других признаков. Эти коэффициенты заключены в переделах –1 и +1.
Для практических расчетов обычно применяют следующую формулу:
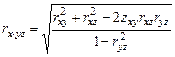 .
.
Аналогично для других зависимостей.
2.3. Регрессия
Корреляционный анализ служит установлению значимости (неслучайности) изменения наблюдаемой случайной величины в процессе испытаний. Следующей, еще более высокой ступенью должно явиться выяснение точных количественных характеристик изменения случайной величины. Подобно тому, как совокупность значений случайной величины описывалась набором неслучайных параметров, так и стохастическую, т.е. содержащую элемент случайности, связь нужно научиться выражать через строгие функциональные (неслучайные) соотношения.
Т.е. требуется установить зависимость некоторой случайной величины У от параметра Х, т.е. у от х, которая называется регрессией. Имеется выборка (х1, у1), (х2, у2),…, (хn, yn) и нужно найти уравнение приближенной регрессии, которое запишем как у = f(x).
В качестве принципа приближенности обычно используют принцип наименьших квадратов, который формулируется так:
Пусть задан некоторый класс функций f(x), накладывающих на выборку одинаковое число связей. Тогда наилучшее уравнение приближенной регрессии дает та функция из рассматриваемого класса, для которой сумма квадратов
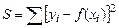
имеет наименьшее значение.
Принцип наименьших квадратов позволяет полностью вычислить уравнение приближенной регрессии заданного типа (с неопределенными коэффициентами). Например уравнение регрессии имеет вид:
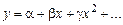
Составляется сумма 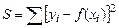 , где функция f(x) записана со всеми неопределенными коэффициентами a, b, g… Величину S можно теперь рассматривать как функцию от этих коэффициентов. Задача состоит в том, чтобы найти набор коэффициентов a, b, g…, минимизирующий величину S. Известно, что необходимым условием минимума функции многих переменных S(a, b, g…) является выполнение равенств вида:
, где функция f(x) записана со всеми неопределенными коэффициентами a, b, g… Величину S можно теперь рассматривать как функцию от этих коэффициентов. Задача состоит в том, чтобы найти набор коэффициентов a, b, g…, минимизирующий величину S. Известно, что необходимым условием минимума функции многих переменных S(a, b, g…) является выполнение равенств вида:
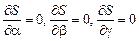 , …
, …
Эти равенства можно рассматривать как уравнения относительно a, b, g…; которые в математической статистике называются нормальными уравнениями.
Доказано, что так как величина S ³ 0 при любых a, b, g…, то у нее обязательно должен существовать хотя бы один минимум и, если система нормальных уравнений имеет единственное решение, то оно и является минимальным для величин S, и никаких дополнительных исследований проводить не нужно.
Используя правила дифференцирования, нормальным уравнениям можно придать следующий вид:
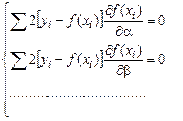
или, после небольших изменений
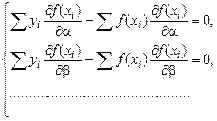
Пример: 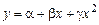 .
.
Тогда 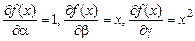 . Поэтому нормальные уравнения имеют вид
. Поэтому нормальные уравнения имеют вид
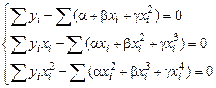 .
.
Относительно неизвестных коэффициентов a, b и g получилась линейная система уравнений третьего порядка; ее нетрудно решить, например, с помощью определителей.
После того, как уравнение найдено, его надо подвергнуть статистическому анализу:
1. Оценить ошибку от замены истинной регрессии приближенной. Проверить значимость всех слагаемых уравнения в сравнении со случайной ошибкой наблюдений.
2. Оценить силу связи (провести корреляционный анализ).
2.3.1. Линейная регрессия
Важный случай регрессии первого порядка 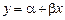 называется парной линейной регрессией. Этот вид зависимости часто встречается в практических расчетах.
называется парной линейной регрессией. Этот вид зависимости часто встречается в практических расчетах.
Так, если об изучаемом явлении нет никаких косвенных сведений, кроме наблюдений, проводимых в настоящий момент, то предварительный характер зависимости можно выяснить, нанося данные в виде точек на координатной плоскости, причем удобнее всего это сделать, предполагая зависимость линейной.
Наконец, во всех сложных случаях, когда регрессия заведомо будет нелинейной, изучение линейной регрессии можно использовать как первый этап исследования, с тем, чтобы в дальнейшем внести в нее необходимые поправки.
Пользуясь принципом наименьших квадратов, легко составить нормальные уравнения линейной регрессии:
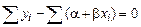
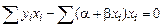 .
.
После простых преобразований приводим систему к виду (m – объем выборки)
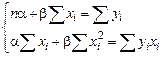 .
.
Число b называется коэффициентом регрессии; его легко найти с помощью определителей:
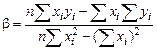 .
.
Число a называется свободным членом регрессии. Его тоже нетрудно найти с помощью определителей, но проще выразить его из первого уравнения через найденное уже b
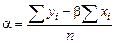 .
.
Полученные формулы полностью определяют линейную регрессию по заданной выборке. Это равенство можно переписать в виде:
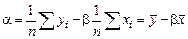 ,
,
откуда
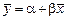 .
.
Таким образом, средняя точка 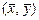 совместного распределения изучаемых величин всегда лежит на линии регрессии. Отсюда вытекает, что для определения линии регрессии достаточно знать лишь ее угловой коэффициент b.
совместного распределения изучаемых величин всегда лежит на линии регрессии. Отсюда вытекает, что для определения линии регрессии достаточно знать лишь ее угловой коэффициент b.
Перейдем к оценке силы найденной связи. Тот факт, что исследуемая зависимость предполагается линейной, позволяет использовать для оценки силы связи выборочный коэффициент корреляции r. Можно показать, что r и b связаны между собой
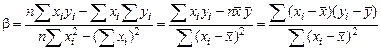
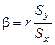 , откуда
, откуда 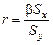
или в развернутом виде
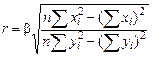 .
.
Если коэффициент корреляции был вычислен ранее, то можно использовать обратную замену b на r.
Мы получим уравнение регрессии в виде
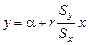
или, заменяя a на 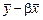 , в виде
, в виде
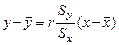 .
.
2.3.2. Нелинейная парная регрессия
Основным способом отыскания уравнения нелинейной регрессии (как и линейной) служит принцип наименьших квадратов. Это значит, что уравнение ищется в заданном классе функций и выборочные числовые данные используются лишь для определения неизвестных коэффициентов из системы нормальных уравнений. При этом различаются 2 случая: тип уравнения фиксируется сразу, так что принцип наименьших квадратов используется лишь один раз, или же уравнение регрессии в дальнейшем подвергается уточнениям, для чего принцип наименьших квадратов последовательно используется несколько раз.
Уравнение регрессии может быть известно заранее из соображений аналогии, из теоретических рассуждений или из сравнения эмпирических данных с известными формулами. Разумеется, никакая уверенность в типе регрессии не освобождает от регрессионного и корреляционного анализа найденного уравнения.
Известно, что любая непрерывная функция может быть со сколь угодно высокой точностью заменена многочленом, при этом повышение точности достигается за счет повышения степени многочлена. Поэтому на практике любую регрессию можно считать в виде многочлена, находя его степень путем последовательных подсчетов.
Но степень может оказаться очень высокой и в уравнении будет много неопределенных коэффициентов. А каждый коэффициент накладывает лишнюю связь на выборку и это увеличивает дисперсию.
Иногда используют регрессию показательного, логарифмического, дробно–степенного, тригонометрического и т.д. типов. Количество коэффициентов при этом сокращается, но подбор вида уравнения гораздо сложнее (нет соответствующего алгоритма).
При подборе формул можно руководствоваться следующими соображениями:
1) В тех случаях, когда с возрастанием одной величины замечается пропорциональное возрастание или убывание другой величины, прежде всего берется уравнение прямой
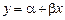 .
.
2) Если с возрастанием одной величины наблюдается резкое возрастание другой, то может быть применимо уравнение показательной кривой
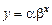 .
.
3) Если, наоборот, с возрастанием одной величины имеется замедленное возрастание другой, то может быть пригодна логарифмическая кривая
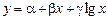 .
.
4) В случае периодического изменения одной величины с возрастанием другой могут быть применимы различные тригонометрические функции.
5) Для дугообразных кривых, имеющих один изгиб и схематически изображенных на рисунке, сравнительно хорошее совпадение может дать парабола 2–го порядка:
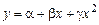 .
.

6) Для кривых S–образной формы, имеющих двойной изгиб, может подойти уравнение параболы 3–го порядка
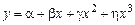 .
.

Вычисление трансцендентной регрессии упрощается, если провести замену переменных, превращающую регрессию в линейную. Например, зависимость показательного типа
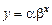
превращается в линейную путем логарифмирования
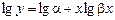 .
.
При использовании кривых, подобранных механически, нужно быть осторожным, во всяком случае нельзя их применять за пределами крайних значений данных, на основе которых вычислены эти уравнения.
2.3.3. Множественная линейная регрессия
Обозначим через Х1 и Х2 независимые переменные, а через У – зависимую случайную величину. Их реализации будут соответственно: х1i, x2i, yi (i = 1, 2, …, m), если m – объем выборки. Предположим, что случайная величина У для любой фиксированной пары значений (х1; х2) распределена по нормальному закону.
Уравнение регрессии ищем в виде
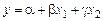 .
.
Оценки для коэффициентов a, b и g получаем, используя метод наименьших квадратов, т.е. обеспечивается выполнение условий:
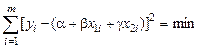 .
.
Приравняв нулю частные производные по a, b и g, получим систему линейных уравнений для определения a, b и g:
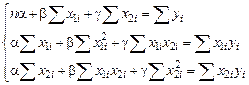 .
.
Преобразование этой системы с учетом обозначений
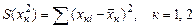
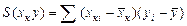
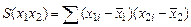
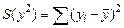
дает оценки коэффициентов a, b, g:
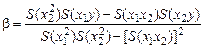 ,
,
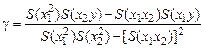 ,
,
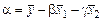 .
.
Коэффициенты b и g являются коэффициентами регрессии(множественные коэффициенты регрессии).
Величина b показывает зависимость значений у от значений х1 при постоянном х2. Поэтому иногда используют обозначение b = 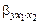 . Соответственно (g =
. Соответственно (g = 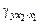 ) выражает зависимость значений у от значений х2 при постоянном х1.
) выражает зависимость значений у от значений х2 при постоянном х1.
Уравнение плоскости регрессии получают в виде 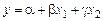 . Оно имеет смысл лишь в определенной области изменения значений х1 и х2.
. Оно имеет смысл лишь в определенной области изменения значений х1 и х2.
Аналогично – при большем количестве х.
2.3.4. Определение параметров уравнения множественной
регрессии методом активного эксперимента
Основа метода – активный спланированный эксперимент – однофакторный и многофакторный (фактор – независимая переменная).
Однофакторный эксперимент состоит в том, что по определенному плану изменяется значение только одного фактора х1 и ведут наблюдение за зависящей от него переменной (функцией отклика у = f(x1, х2…)). Остальные факторы х2, х3,… поддерживаются без изменений на одном базовом уровне. Затем та же схема повторяется со вторым фактором х2 и т.д. После каждой серии опытов рассчитывают «свой» коэффициент регрессии, а затем окончательно находят общее выражение для функции 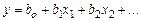 Недостатком такого подхода является то, что требуется проведение большого количества опытов, кроме того метод не позволяет учитывать эффекты взаимного влияния факторов.
Недостатком такого подхода является то, что требуется проведение большого количества опытов, кроме того метод не позволяет учитывать эффекты взаимного влияния факторов.
Чаще применяют многофакторный активный эксперимент, при проведении которого в каждом опыте изменяют значения всех факторов. При этом сокращается число опытов, и задача решается при минимальных затратах времени и средств.
Суть метода
Ищется уравнение регрессии линейного вида
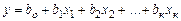 , (*)
, (*)
где х1, х2,…, хк – варьируемые факторы, они поддерживаются на двух заранее выбранных фиксированных уровнях.
Верхний уровень хi,max кодируется через +1, нижний – хi,,min – через -1. Соотношение между натуральными и кодированными переменными имеет вид
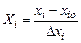 ,
,
где хi – натуральная переменная (хi = хi,max или хi = хi,min);
Хi – кодированная переменная (+1 или -1);
хiо – средний (нулевой) уровень, около которого осуществляется варьирование;
Dхi – интервал (шаг) варьирования по отношению к хiо;
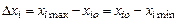 >0.
>0.
Число опытов определяется из соотношения N = 2к, где к – число варьируемых факторов.
Следовательно, при двух факторах минимальное число опытов (без повторения) равно 4, при трех факторах - 8 и т.д.
Матрицы планирования для этих случаев приведены соответственно в табл. 1 и 2.
Таблица 1
Два фактора
| Номер опыта | Х1 | Х2 | у | Номер опыта | Х1 | Х2 | у | |
| -1 | -1 | у1 | -1 | +1 | у3 | |||
| +1 | -1 | у2 | +1 | +1 | у4 |
Таблица 2
Три фактора
| Номер опыта | Х1 | Х2 | Х3 | у | Номер опыта | Х1 | Х2 | Х3 | у | |
| -1 | -1 | -1 | у1 | -1 | -1 | +1 | у5 | |||
| +1 | -1 | -1 | у2 | +1 | -1 | +1 | у6 | |||
| -1 | +1 | -1 | у3 | -1 | +1 | +1 | у7 | |||
| +1 | +1 | 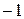
| у4 | +1 | +1 | +1 | у8 |
Как можно заметить, матрица так называемого полного факторного эксперимента (ПФЭ) строится по принципу – ни одной повторяющейся комбинации уровней факторов. Удобно использовать правило: матрица эксперимента 23 получается путем повторения матрицы эксперимента 22 при нижнем (-1) , а затем при верхнем (+1) значении нового фактора Х3.
При возрастании числа факторов число опытов может стать довольно большим. Так, для шести факторов число необходимых опытов равно 64.
Следует отметить, что при полном факторном эксперименте имеется возможность определить коэффициенты не только для уравнения регрессии линейного вида
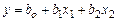 ,
,
но и для уравнения, отражающего взаимодействия факторов, например
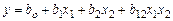 .
.
Для сокращения числа опытов часто используют дробный факторный эксперимент (ДФЭ). Идея состоит в том, что, если из каких–либо соображений можно пренебречь необходимостью определения коэффициентов при некоторых факторах или их взаимодействиях, то реализуется не вся матрица ПФЭ, а например половинная, четвертная, восьмая и т.д. часть полной матрицы.
Рассмотрим методику организации ПФЭ.
Прежде чем приступить к реализации матрицы планирования необходимо выбрать для каждого фактора опорный (нулевой) уровень хiо и интервал варьирования Dхi, что позволит определить нижнее и верхнее значения уровня каждой их всех варьируемых переменных.
После того как составлена матрица планирования и выбраны уровни варьирования факторов можно перейти к постановке опытов, в каждом из которых должна быть реализована одна из строк матрицы. При этом кодированному значению переменной (-1) соответствует нижний уровень варьируемого фактора, а значению (+1) – верхний уровень.
Для устранения предвзятости или субъективизма исследователя, а также систематических ошибок, связанных, например, с разогревом или охлаждением агрегатов и приборов во время эксперимента, старением катализатора, опыты проводятся не в очередности, соответствующей их порядковому номеру в матрице планирования, а в случайном порядке, называемом порядком рандомизации. Порядок рандомизации может быть, например, разыгран путем вытаскивания номеров опытов из урны.
В результате реализации на объекте каждого из опытов заполняется последний столбец матрицы, т.е. записываются значения выходной величины у, полученные при проведении соответствующих вариантных опытов (строк матрицы).
Важным условием получения достоверных результатов является воспроизводимость опытов. Поэтому на каждом уровне могут проводить несколько опытов. Эта процедура называется проверкой воспроизводимости и осуществляется с использованием специального критерия. Необходимо подчеркнуть, что проверка воспроизводимости является важнейшей предпосылкой, лишь при выполнении которой результатам опытов и полученным на их основе закономерностям можно доверять.
При реализации опытов в соответствии с матрицей планирования и поверки воспроизводимости можно приступить к расчету коэффициентов уравнения регрессии. Благодаря переходу к кодированным переменным, которые принимают лишь два значения (-1) (+1), и специальному планированию экспериментов коэффициенты уравнения регрессии определяются раздельно, независимо друг от друга и по очень простой формуле.
Например, коэффициент bi при i–ом факторе хi:
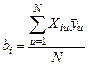 ,
,
где N – число вариантов опытов в матрице планирования;
Хiu – значение кодированной переменной в u–той строке, i–того столбца, равное либо (-1), либо (+1);
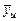 – среднее значение выхода для u–того варианта опыта (строки).
– среднее значение выхода для u–того варианта опыта (строки).
Отсюда видно, что расчет коэффициентов сводится к простому алгебраическому суммированию построчных значений выходов со знаками столбца, соответствующего данному фактору, и делению на число вариантов опытов. Например, коэффициент при переменной Х1 для уравнения (*) с использованием табл. 1 определяется следующим образом:
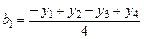 .
.
Коэффициент bо по физическому смыслу соответствует опыту с поддержанием всех варьируемых факторов на средних (опорных) уровнях
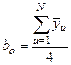 , т.е.
, т.е. 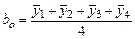 .
.
Недостатком активного метода является условие управляемости процессом по каждому из варьируемых факторов, т.е. возможность независимого изменения каждого из этих факторов и поддержания его на заданном уровне в период проведения опыта.
Дата добавления: 2016-03-27; просмотров: 2064;
