Вторая дисперсия может также быть найдена усреднением в виде

1 _k

s_W² = S (N_i - 1) s_i² . (2.10)

N - k ^{i = 1}

- 23 -

В ситуации, когда s_B² неслучайно превышает s_W² , можно констатировать существование достоверной межвыборочной изменчивости средних значений признака в k генеральных совокупностях, из которых взяты k выборок. Сравнение двух дисперсий производится с применением обычного F-критерия Фишера.

2.6 В многомерном случае для проверки существования неслучайной межвыборочной вариации средних уровней набора признаков X₁, X₂, X₃, ..., X_m используется сходный способ рассмотрения данных, называемый многомерным дисперсионным анализом. Пусть мы рассматриваем k выборок с числами наблюдений в них N₁, N₂, N₃, ..., N_k . Для каждой из этих выборок по набору m признаков были найдены векторы средних M₁, M₂, M₃,..., M_k и ковариационные матрицы S₁, S₂, S₃,..., S_k . По всем N = N₁ + N₂ + N₃ + ... + N_k наблюдениям, можно найти общий вектор средних

1 _k

M_o = S N_iM_i . (2.11)

N ⁱ⁼¹

Точно также как в одномерном случае, когда общая вариация по отдельному признаку описывалась суммой Q_o, находимой по формуле (2.7), многомерная изменчивость, проявляющаяся во всем материале, может быть измерена аналогичной матрицей

S (X_1ij - M_1o)² ... S (X_1ij - M_1o) (X_mij - M_mo)

^{i, j i, j}

T= ... ... ... . (2.12)

S (X_1ij - M_1o) (X_mij - M_mo) ... S (X_mij - M_mo)²

^{i, j i, j}

Здесь диагональные элементы описывают общую изменчивость по каждому из m признаков, внедиагональные элементы – измеряют общую соотносительную вариацию по всем парам признаков. Первый подписной индекс соответствует номеру признака (1, 2, ..., m), второй (i) - номеру выборки (1, 2, ..., k), третий (j) - номеру наблюдения (1, 2, ..., N). Суммирование ведется по всем N наблюдениям, имеющимся в k выборках. Нетрудно видеть, что каждый диагональный элемент матрицы T точно соответствует сумме (2.7).

Межгрупповая изменчивость набора признаков X₁, X₂, X₃, ..., X_m может быть измерена многомерным аналогом суммы Q_B - матрицей

S N_i (M_1i - M_1o)² ... S N_i (M_1i - M_1o)(M_mi - M_mo)

^{i i}

B = ... ... ... . (2.13)

S N_i (M_1i - M_1o)(M_mi - M_mo) ... S N_i (M_mi - M_mo)²

^{i i} Здесь каждый диагональный элемент описывает многомерную межгрупповую вариацию по отдельному признаку и точно соответствует одномерной сумме Q_B

- 24 -

для него. Внедиагональные элементы матрицы B описывают соотносительную вариацию средних величин по всем парам признаков. Суммирование ведется по всем k выборкам.

Внутригрупповая вариация набора признаков X₁, X₂, X₃, ..., X_m может быть описана многомерным аналогом суммы Q_W - матрицей

S (X_1ij - M_1i)² ... S (X_1ij - M_1i)(X_mij - M_mi)

^{i, j i, j}

W = ... ... ... . (2.14)

S (X_1ij - M_1i)(X_mij - M_mi) ... S (X_mij - M_mi)²

^{i, j i, j}

Каждый диагональный элемент матрицы W точно соответствует одномерной сумме Q_W и измеряет суммарную внутривыборочную вариацию для отдельного признака. Внедиагональные элементы этой матрицы описывают соотносительную внутривыборочную изменчивость для всех попарных сочетаний признаков. Суммирование везде проводится для всех наблюдений и по всем выборкам.

Для трех матриц T, B и W выполняется равенство

T = B + W . (2.15)

На основе каждой из них может быть найдена соответствующая ковариационная матрица. В частности, межгрупповая ковариационная матрица

s _B11 s _B12 s _B13 ... _.s_B1m

Bs_B12 s_B22 s_B23 ... s_B2m

S_B = = s_B13 s_B23 s_B33 ... s_B3m (2.16)

k - 1 ... ... ... ... ...

s _B1m s_B2m s_B3m ... s_Bmm

на главной диагонали включает межгрупповые дисперсии отдельных признаков (f = 1, 2, 3, ..., m), находимые по обычной формуле одномерного дисперсионного анализа

1 _k

s_Bff = S N_i (M_if - M_of)² , (2.17)

k - 1 ^{i = 1}

а внедиагональными элементами являются межгрупповые ковариации для всех попарных сочетаний признаков (f ¹ h)

1 _k

s_Bfh = S N_i (M_if - M_of) (M_ih - M_oh) (2.18)

k - 1 ^{i = 1}

Аналогичным образом, внутригрупповая ковариационная матрица

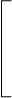s_W11 s_W12 s_W13 ... s_W1m

Ws_W12 s_W22 s_W23 ... s_W2m

S_W = = s_W13 s_W23 s_W33 ... s_W3m (2.19)

N - k ... ... ... ... ...

s_W1m s_W2m s_W3m ... _. s_Wmm

- 25 -

является простой ковариационной матрицей, но опирающейся на данные всех выборок. Ее можно также получить взвешенным усреднением всех ковариационных матриц S₁, S₂, S₃, ..., S_k по всем k выборкам

1 _k

S_W = S (N_i - 1) S_i . (2.20)

N - k ^{i = 1}

Такое усреднение, как и вообще получение единой внутригрупповой ковариационной матрицы, возможно только, если для всех выборок наблюдается однородность внутригрупповой изменчивости, т. е. соблюдается так называемая гомоскедастичность. Ковариационные матрицы S_B и S_W являются многомерными аналогами межгрупповой и внутригрупповой дисперсий одномерного дисперсионного анализа.

Разумеется, формулы (2.17) и (2.18) не слишком удобны для нахождения элементов межгрупповой ковариационной матрицы S_B или матрицы сумм B. Для любого диагонального элемента последней - можно использовать формулу

_k 1 _k 2

b_ff = S N_iM_fi² - S N_iM_fi .

^{i = 1} N ^{i = 1}