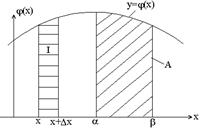
Геометрическое истолкование этой формулы

Из (*) вытекает, что с точностью до бесконечно малых величин высшего порядка по сравнению с Dх справедливо равенство:

.

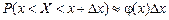Это произведение геометрически изображается площадью прямоугольника I.

Вероятность того, что случайная величина примет значения внутри участка (a, b), выражается площадью криволинейной трапеции А – в этом состоит геометрический смысл выражения (**).

Известно, что j(х) ³ 0, так как F(x) – монотонно неубывающая функция, а из формулы следует (**) .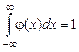

Легко установить выражение функции распределения через плотность вероятности. F(x) - есть первообразная от j(х), причем такая, которая обращается в нуль при 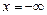. Поэтому

.

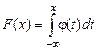Физическая интерпретация:

F(x) – Представим единицу массы, распределенную вдоль прямой так, чтобы количество массы, сосредоточенное во всех точках прямой, для которых Х £ х, т.е. находится слева от точки х, равнялось F(x).

Тогда j(х) будет представлять собой плотность единичной массы в рассматриваемой точке.

Числовые характеристики случайных величин - это такие характеристики, которые одновременно связаны с функциями распределения, но которые могут быть найдены даже тогда, когда F(x) или j(x) неизвестны, и которыми удобно пользоваться при решении прикладных задач. К числу таких характеристик относятся средние значения и моменты случайных величин.