Числовые характеристики

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

СЕВЕРО–КАВКАЗСКИЙ ГОРНО–МЕТАЛЛУРГИЧЕСКИЙ ИНСТИТУТ

(ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ)

Кафедра теории и автоматизации металлургических

Процессов и печей

МАТЕМАТИЧЕСКИЕ ОСНОВЫ АВТОМАТИКИ

Допущено редакционно–издательским советом Северо–Кавказского горно–металлургического института (государственного технологического университета) в качестве конспекта лекций для студентов

специальности 22301.65

«Автоматизация технологических процессов и производств»

(по отраслям)

Владикавказ 2008

УДК 519.71:681.5

Рецензент: Рутковский А. Л.

Текиев В. М.

Математические основы автоматики: Конспект лекций. –Вла­дикавказ: Издательство СКГМИ (ГТУ) "Терек", 2008. с.

Редактор Иванченко Н. К.

Компьютерная верстка Цишук Т. С.

УДК 519.71; 681.5

Ó Издательство СКГМИ (ГТУ) "Терек", 2008

Сдано и подписано в печать 28.10.08. Формат 60x84 1/₁₆. Объем 5,39 усл. п.л.

Тираж 75 экз. Заказ №

Отдел оперативной полиграфии СКГМИ (ГТУ).

362021. Владикавказ, ул. Николаева, 44.

Тема 1. Случайные события и случайные величины, их

числовые характеристики

1.1. Математические модели эксперимента, учитывающие случайный разброс его результатов

Все процессы, происходящие в природе, являются результатом взаимодействия многих факторов. Для того чтобы изучить эти процессы и в дальнейшем ими управлять, необходимо выяснить, какую роль в рассматриваемом процессе играет каждый фактор в отдельности. Все эти факторы необходимо выразить в каких–либо количественных оценках. Для этого используют математические методы и чтобы получить необходимые числовые данные, нужно произвести серию наблюдений.

Однако даже самый тщательно подготовленный эксперимент не позволяет выделить интересующий нас фактор в чистом виде. Мы не в силах изолировать многие посторонние факторы: изучая химические реакции, мы никогда не имеем дела с чистыми веществами; изучая электронные процессы, не можем вести их в абсолютном вакууме и т.д. Наконец, нужно вспомнить о различных помехах, связанных с окружающей обстановкой – ведь даже шум идущего по улице автомобиля сказывается на проводимом в лаборатории эксперименте.

Следовательно, каждое наблюдение дает нам лишь результат взаимодействия основного изучаемого фактора с многочисленными посторонними. Некоторые их этих факторов можно учесть, так как они сами по себе достаточно изучены. Учет других факторов (например, наличие примесей в веществах) может быть очень громоздким. Он сильно затягивает эксперимент, делает его неоправданно дорогим. Наконец, многие факторы (помехи) бывают настолько неожиданными, что их вообще нельзя учесть. Сюда следует отнести и те факторы, о которых на данном этапе развития науки вообще ничего не известно.

Вывод: полное и точное описание какого–либо процесса возможно лишь в том случае, если известны все факторы, влияющие на этот процесс. Иными словами, такое описание вообще невозможно.

К счастью, оно и не нужно!

Так все применяемые в эксперименте измерительные приборы обладают некоторым пределом точности – минимальной разницей в значениях двух величин, которую они в состоянии обнаружить. Этот предел обычно указывается на приборах, изготовленных в заводских условиях. Например, аналитические весы, взвешивающие с точностью до 0,1 мг, не смогут различить такие веса, как 12,52 и 12,54 мг, и в обоих случаях покажут 12,5 мг. В результате все дальнейшие вычисления, связанные с этими данными, также будут содержать некоторую неточность, даже если пользоваться абсолютно точными и полными формулами, описывающими исследуемый процесс.

Таким образом, в наших наблюдениях всегда допускается некоторая «законная» неточность, величину которой можно рассчитать заранее. Благодаря этому мы можем не учитывать те посторонние факторы, действие которых намного меньше этой неточности. По этой же причине удается избежать детального исследования многочисленных непредвиденных (случайных) помех. Хотя действие каждой из них может оказаться вполне заметным, в общей массе они как правило, уравновешивают друг друга, лишь изредка давая заметный суммарный эффект.

Установлено, что случайные, непредвиденные события в массе своей подчиняются некоторым общим неслучайным закономерностям. Наука, изучающая закономерности массовых случайных явлений, называется теорией вероятностей. Применение теории вероятностей к обработке больших совокупностей чисел называется математической статистикой.

Использование методов математической статистики в обработке наблюдений оказывается весьма плодотворным. Никакие теории при наличии непредвиденных и случайных факторов не могут давать точные и однозначные ответы. Основная задача математической статистики при обработке наблюдений – оценить риск той или иной ошибки в полученном результате. Принять или не принять риск – дело исследователя. В том случае, если этот риск его не устраивает, он должен найти пути его уменьшения: применить более точную методику наблюдений, устранить наиболее заметные помехи и т.д.

Теория вероятностей отвлекается от всех физических особенностей изучаемого явления, кроме его случайности. Поэтому применение теории вероятностей к обработке наблюдений приводит нередко к очень грубым оценкам и ее выводы следует использовать очень осторожно, в то же время применение этих методов почти всегда связано с большим объемом вычислений.

К категории случайных явлений можно отнести все те явления, точное предсказание протекания которых в каждом отдельном случае оказывается невозможным. Однако, если вместо того, чтобы рассматривать каждое из случайных явлений в отдельности, мы обратимся к совокупности большого их числа, то окажется, что средние результаты обнаруживают своего рода устойчивость.

В теории вероятностей рассматриваются три класса случайных явлений: случайные события; случайные величины; случайные функции.

Случайные события

Событие, которое при заданном комплексе факторов может либо произойти, либо не произойти, называется случайным событием.

Примеры: 1. Выпадение герба при бросании монеты.

2. Попадание в цель при выстреле.

Различные события мы будем обозначать буквами А, В, …

Событие называют достоверным, если оно непременно должно произойти. Например – появление электрического тока в замкнутой цепи с хорошим источником ЭДС.

Событие называют невозможным, если оно заведомо не наступит. Пример: ток в разомкнутой цепи.

Пусть А – некоторое событие. Под событием, противоположным ему будем понимать событие, состоящее в том, что А не наступило, обозначим его 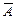. События А и В называют несовместными, если наступление одного из них исключает возможность наступления другого. Например: появление четного и нечетного чисел одновременно при бросании кости невозможно.

Событие называют единственно возможным, если в результате каждого испытания хотя бы одно из них наверное наступит. Эти события образуют полную группу событий.