Безусловная оптимизация управления
Одним из наиболее простых методов решения задачи безусловной оптимизации является метод Ньютона. Для этого целевую функцию дифференцируют в частных производных и приравнивают эти производные к нулю.
Пусть имеется зависимость
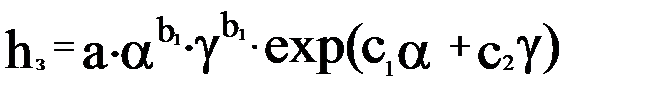 .
.
Найти такие значения a и g , при которых hз = min. Дифференцируя в частных производных, получим
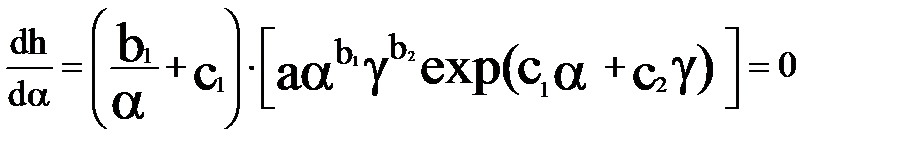 ;
;
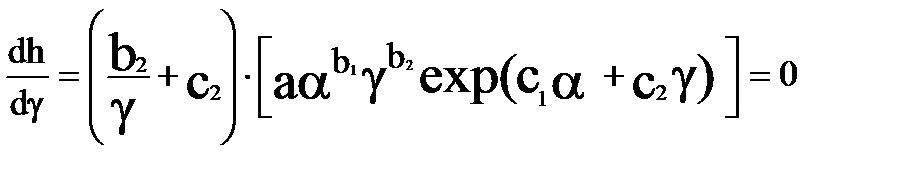 .
.
Так как 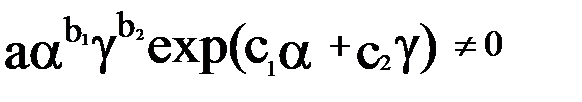 , то
, то 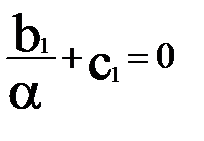 ;
; 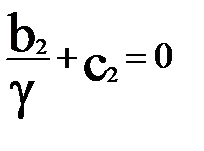 .
.
Отсюда 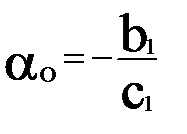 ;
; 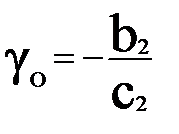 .
.
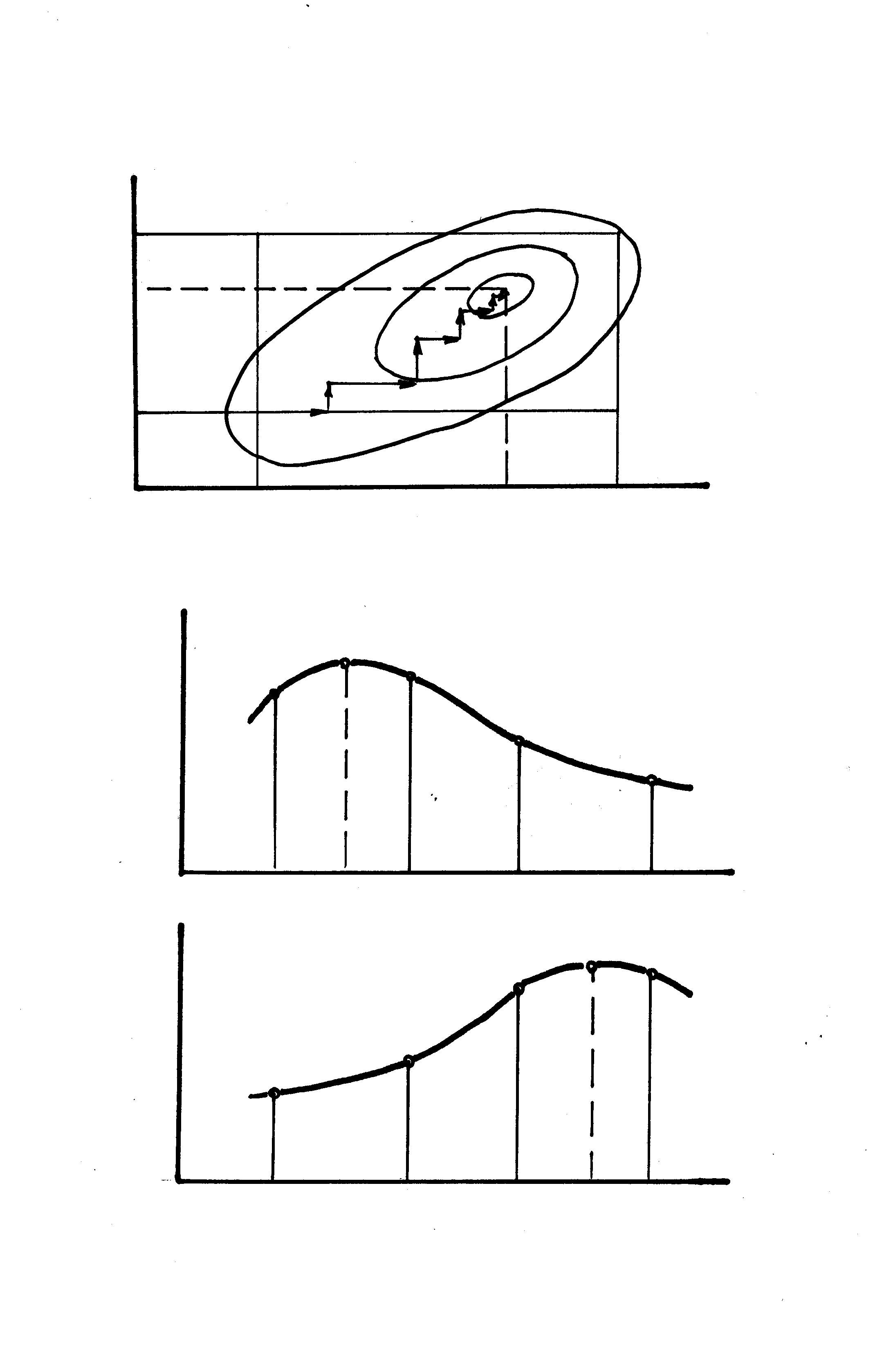
Другим методом решения задачи безусловной оптимизации является покоординатный метод.
Покоординатный метод определения максимума функции нескольких переменных в области [z 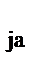 , z
, z 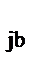 ] включает в себя многократное решение (поочередно для каждой переменной) задачи определения максимума функции одной переменной.
] включает в себя многократное решение (поочередно для каждой переменной) задачи определения максимума функции одной переменной.
Максимум функции одной переменной определяется методом золотого сечения. Для этого в области [z 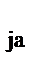 , z
, z 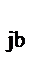 ], на которой решается задача оптимизации, задается начальная точка z
], на которой решается задача оптимизации, задается начальная точка z 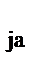 , а целевая функция рассматривается при фиксированных значениях всех факторов кроме одного, изменяющегося в пределах
, а целевая функция рассматривается при фиксированных значениях всех факторов кроме одного, изменяющегося в пределах
z 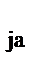
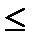 z
z 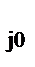
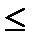 z
z 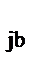 .
.
Устанавливают два значения этого фактора, равные
z 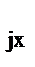 = 0,618 z
= 0,618 z 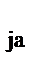 + 0,382 z
+ 0,382 z 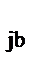 ;
;
z 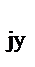 = 0,382 z
= 0,382 z 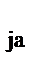 + 0,618 z
+ 0,618 z 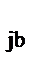 .
.
Затем вычисляют соответствующие им значения целевой функции
R 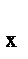 = F(z
= F(z 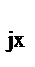 ) и R
) и R 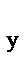 = F(z
= F(z 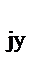 )
)
и сравнивают их между собой.
Если R 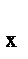 > R
> R 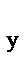 , то z
, то z 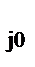 < z
< z 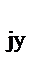 . Тогда оптимум фактора z
. Тогда оптимум фактора z 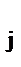 должен лежать в пределах z
должен лежать в пределах z 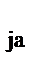
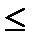 z
z 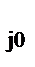
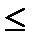 z
z 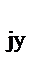 , а z
, а z 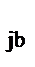 присваивается значение, равное
присваивается значение, равное
z 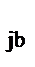 = z
= z 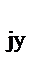 ,
,
Если R 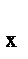 < R
< R 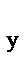 , то z
, то z 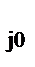 > z
> z 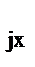 . Тогда оптимум фактора z
. Тогда оптимум фактора z 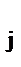 должен лежать в пределах
должен лежать в пределах
z 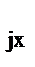
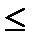 z
z 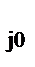
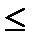 z
z 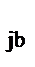 ,
,
а z 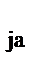 присваивается значение, равное
присваивается значение, равное
z 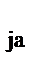 = z
= z 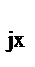 .
.
Сужение пределов осуществляется последовательно до тех пор, пока разность верхней и нижней границ не будет превышать точности вычислений.
Оптимум фактора z 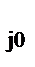 определяется как полусумма верхней и нижней границ
определяется как полусумма верхней и нижней границ
z 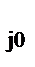 = (z
= (z 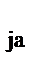 + z
+ z 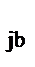 ) / 2 .
) / 2 .
Это значение принимают за начальное при определении оптимума следующего фактора z 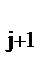 .
.
В результате каждого шага начальная точка перемещается ближе к оптимуму. Этот процесс продолжается до тех пор, пока разность между начальной и конечной точками не будет меньше точности вычислений.
| z2 z2b z2o z2a z1а z1о z1b z1 Рис 9. Покоординатный метод определения экстремума R Rx > Ry zа zо zx zy zb z R Rx < Ry zа zx zy zо zb z Рис. 10. Определение максимума методом золотого сечения |
Дата добавления: 2016-03-15; просмотров: 1156;
