Методы решения задач управления
Решением задач оптимального управления физическими процессами занимается математическое программирование, т.е. раздел математики, в котором изучаются методы нахождения экстремумов функций многих переменных при наличии дополнительных ограничений на эти переменные, имеющих форму равенств или неравенств.
В основе оптимального управления лежит принцип максимума Понтрягина, дающий общее необходимое условие оптимальности. Условием оптимальности является максимум некоторой функции многих переменных, характеризующей качество управления.
Математическое программирование включает в себя линейное программирование, нелинейное программирование (в том числе выпуклое и квадратичное программирование), динамическое программирование (для многошаговых процессов), дискретное программирование, стохастическое программирование и параметрическое программирование.
Чаще всего для решения задач управления физическими процессами используют методы линейного, нелинейного и стохастического программирования. Решение таких задач может осуществляться также методом безусловной оптимизации.
Безусловная оптимизация – раздел математики, в котором изучаются методы нахождения экстремумов функций многих аргументов при отсутствии дополнительных ограничений на эти аргументы.
Нелинейное программирование - раздел математического программирования, в котором изучаются методы нахождения условных экстремумов нелинейных функций многих аргументов при наличии дополнительных нелинейных ограничений на эти аргументы, имеющих форму равенств.
Линейное программирование - раздел математического программирования, в котором изучаются методы нахождения условных экстремумов линейных функций многих переменных при наличии дополнительных линейных ограничений на эти переменные, имеющие форму неравенств.
Стохастическое программирование - раздел математического программирования, в котором изучаются методы нахождения условных экстремумов функций многих аргументов при заданной вероятности выполнения дополнительных ограничений на эти аргументы.
Информация о методе решения задачи управления определяется информацией о цели и эффективности управления.
Метод безусловной оптимизации применяется в случаях, когда целевая функция имеет локальный или глобальный экстремум.
Метод нелинейного программирования применяется в тех случаях, когда целевая функция и ограничения являются нелинейными, а сама целевая функция экстремума не имеет.
Метод линейного программирования применяется в тех случаях, когда целевая функция и ограничения являются линейными или нелинейными, которые путем преобразования приводят к линейным. Например, в случае использования степенных мультипликативных функций
R 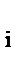 = c
= c 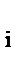
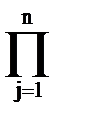
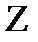
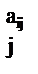 ,
,
которые путем логарифмирования приводят к линейным полиномиальным
ln R 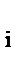 = ln c
= ln c 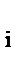 +
+ 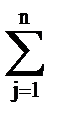 a
a 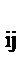 ln zj .
ln zj .
Метод стохастического программирования применяется в случаях, когда параметры физического процесса являются случайными функциями, а ограничения на параметры заданы вероятностями их выполнения, т.е. в случаях обеспечения надежности управляемого физического процесса.
Задачи управления
Всякая задача оптимального управления состоит в выборе среди множества допустимых решений (допустимых управляющих воздействий) такого, которое в некотором смысле можно квалифицировать как оптимальное.
Допустимые решения – это решения, которые находятся внутри области управления и удовлетворяют всем без исключения ограничениям, накладываемым целью управления.
Оптимальное решение – это решение, которое находится на границе области допустимых решений и обеспечивает максимальное значение целевой функции.
Допустимость каждого решения понимается как в смысле возможности его фактического осуществления, так и в смысле достижения цели управления, а оптимальность – в смысле его максимальной эффективности.
Задача управления формулируется следующим образом: внутри области управления определить такое сочетание значений управляющих факторов zj, которое обеспечивает максимальную эффективность управления, задаваемую целевой функцией этих факторов, при наличии или отсутствии дополнительных ограничений в виде равенств или неравенств на зависимые от этих факторов параметры Ri.
Существующие методы решения позволяют решать следующие задачи управления: безусловной оптимизации, нелинейного программирования, линейного программирования и стохастического программирования.
Задача безусловной оптимизации формулируется следующим образом: пусть дана нелинейная целевая функция F(zj), имеющая экстремум в некоторой точке zjo . Найти такие значения переменных zjо, которые обеспечивают максимальную эффективность физического процесса, заданную этой функцией
F(zj) = max, j = 1 ... n.
Целевые функции могут быть представлены в виде экспоненциально-степенных мультипликативных функций вида
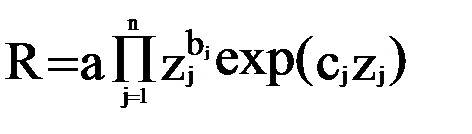
или квадратных полиномиальных функций вида
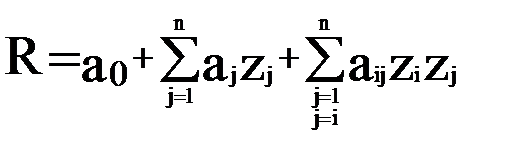 .
.
Задача нелинейного программирования формулируется следующим образом: максимизировать нелинейную целевую функцию
Fo(zj) = max, j = 1 ... n ,
с помощью которой проводится оценка эффективности управления, при линейных ограничениях - равенствах
Fi(zj) – [Ri] = 0, i = 1 ... m-1,
накладываемых на решение задачи целью управления.
Задача линейного программирования формулируется следующим образом: максимизировать линейную или логарифмически линейную целевую функцию
Fo(zj) = max или Fo(ln zj) = max, j = 1 ... n,
с помощью которой оценивается эффективность управления при заданных условиях выполнения линейных или логарифмически линейных ограничениях – неравенствах
Fi(zj) – [Ri] £ 0 или Fi(ln zj) – ln [Ri] £ 0, i = 1 ... m-1,
накладываемых на решение задачи целью управления.
Задача стохастического программирования формулируется следующим образом: максимизировать линейную или логарифмически линейную целевую функцию
Fo(zj) = max или Fo(ln zj) = max, j = 1 ... n,
с помощью которой оценивается эффективность управления при заданной вероятности выполнения линейных или логарифмически линейных ограничений – неравенств
Prob{Fi(zj) £ [Ri]} ³ F(Ri), i = 1 ... m-1
или
Prob{Fi(ln zj) £ ln [Ri]} ³ F(Ri), i = 1 ... m-1,
накладываемых на решение задачи целью управления.
Задача стохастического программирования заключается в определении таких значений переменных z 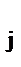 , которые обеспечивают максимальную эффективность управления, задаваемую целевой функцией
, которые обеспечивают максимальную эффективность управления, задаваемую целевой функцией
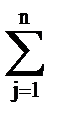 a
a 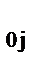 ln z
ln z 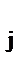 = max, j = 1 ... n
= max, j = 1 ... n
при заданной вероятности соблюдения установленных ограничений на параметры процесса
P ( 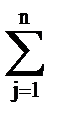 a
a 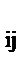 ln z
ln z 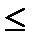 ln ([R
ln ([R 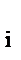 ]/c
]/c 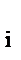 )) > F(R
)) > F(R  ), i = 1 ... m .
), i = 1 ... m .
Такая задача не может быть решена непосредственно. Возможным путем решения этой задачи является переход к детерминированному эквиваленту. В основе перехода лежит использование закона распределения случайного параметра.
Дата добавления: 2016-03-15; просмотров: 1068;
