Математические модели случайных процессов

Если физический процесс находится под воздействием большого числа неконтролируемых случайных возмущающих факторов, то он является случайным процессом, а состояние его описывается случайными параметрами.

Случайные параметры процесса оцениваются функциями распределения F(R). Для описания случайного процесса используют различные функции распределения. С практической точки зрения необходимо стремиться к модели простой, точной и справедливой на всей области управления.

Экспоненциальное распределение случайного фактора характерно для таких физических величин, значения которых тяготеют к некоторому среднему значению ω_о.

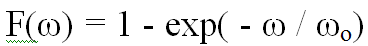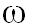( - случайный фактор процесса).

Степенное распределение случайного фактора характерно для таких физических величин, значения которых тяготеют к крайнему значению.

.

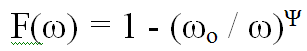Пусть некоторый параметр процесса R является степенной мультипликативной функцией нескольких определенных управляющих факторов z_j и нескольких случайных возмущающих факторов ω_k

.

Так как реализуемые на практике значения случайных факторов имеют тенденцию к группированию вокруг некоторого среднего, то было бы логично принять распределение случайных факторов экспоненциальным

.

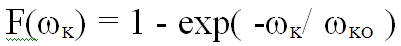Путем соответствующих преобразований получаем функцию распределения случайного параметра, зависящего от р случайных факторов w и n определенных факторов z .

,

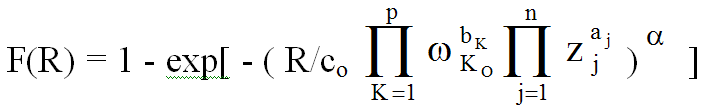где a - показатель распределения параметра, равный величине, обратной сумме степеней влияния случайных факторов на этот параметр

.

Так как значения случайных возмущающих факторов не требуют определения при решении задачи управления, то их можно исключить, положив

.

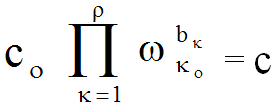Тогда функция распределения параметра процесса R, т.е. вероятность появления значения параметра процесса, не превышающего R при заданных значениях управляющих факторов z , примет вид

,

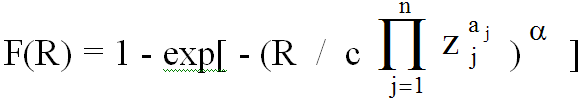где с – коэффициент; а - экспоненты; a - показатель распределения.

Данная функция является основой для построения стохастических моделей.

Так как параметры процесса закономерно изменяются с течением времени, то процесс является нестационарным, а время - одним из факторов. Воздействие этого фактора объективно вызывает изменение состояния управляемого объекта.

Динамическая модель процесса позволяет принять такое решение об управляющем воздействии, реализация которого обеспечивает желаемое изменение состояния управляемой системы к определенному моменту времени.

Стохастическая динамическая математическая модель процесса представляет собой систему математических соотношений между вероятностями появления значений параметров процесса R при определенных значениях управляющих факторов z_j , в том числе и
времени T.