Метод наименьших квадратов. Параметрическая идентификация для рассмотренных видов математических моделей осуществляется с использованием метода наименьших квадратов

Параметрическая идентификация для рассмотренных видов математических моделей осуществляется с использованием метода наименьших квадратов, т.к. при известных значениях управляющих факторов и реализованных в эксперименте значениях параметров имеющиеся зависимости можно привести к линейному виду.

Пусть имеется некоторая совокупность из р реализованных в эксперименте значений х_к и у_к. Предполагается, что искомая зависимость описывается линейной функцией вида

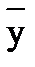= с + а х .

Требуется установить такие значения коэффициентов с и а, при которых сумма квадратов отклонений, наблюдаемых в эксперименте значений у от расчетных 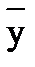, была бы минимальной.

Расчетные значения у в каждом опыте равны:

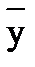₁ = с + а х₁

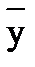₂ = с + а х₂

...…….........

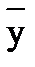_р = с + а х_р .

Отклонения значений в каждом опыте равны:

e₁= 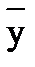₁ – у₁ = с + а х₁ – у₁

e₂= 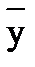₂ – у₂ = с + а х₂ – у₂

……………………………

e_р= 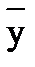_р – у_р = с + а х_р – у_р .

Изменение значений коэффициентов с и а приводит к увеличению или уменьшению отклонений, обобщенным показателем которых является величина

Е =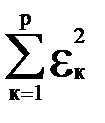

или

Е = .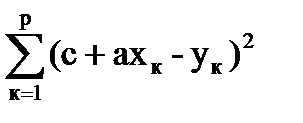

Условием Е = min является

;

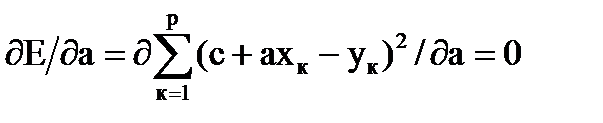
или

;

.

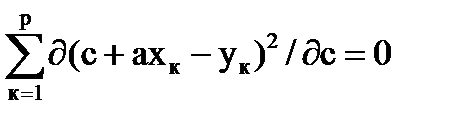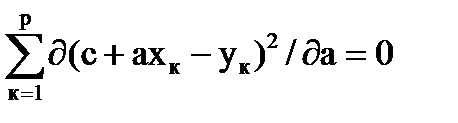Дифференцируя в частных производных, получим

;

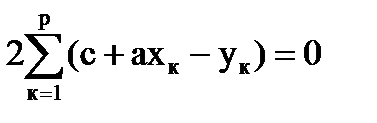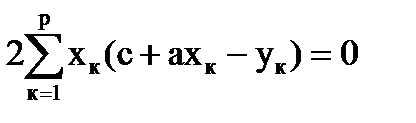
или

;

.

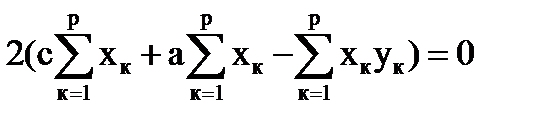Полученную систему уравнений можно представить в виде

;

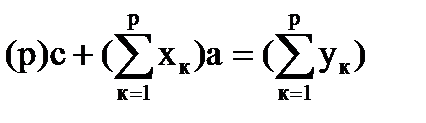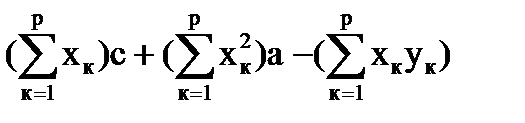
или в матричной форме:

*

=

.

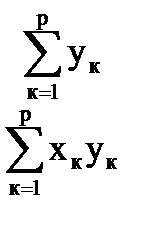
Решив систему уравнений, получают значения коэффициентов с и а.

Показатели распределения в математической модели 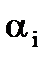определяют следующим образом. Для каждого опыта вычисляют отклонения наблюдаемых в эксперименте значений параметров от расчетных значений

ln 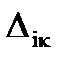= ln R 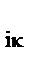- (ln c + ) .

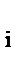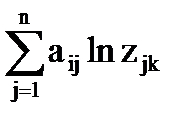Полученные отклонения ранжируются по возрастающей. Показатели распределения a_i вычисляют по формуле

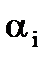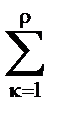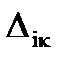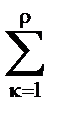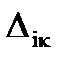= (ln )(ln ln((p+0,4)/(p-k+0,7))/ (ln )² .

где k - номер по возрастающей ln ;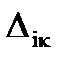

p - число опытов.

Так как в расчет принимают не вероятность события, а его частоту, то при ограниченном числе опытов вводится коррекция в виде поправочных коэффициентов 0,4 и 0,7, приближающая частоту к вероятности. Иными словами, так как вероятность не равна частоте n/N 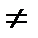k/p, а только стремится к ней при p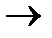 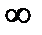, то принимают n/N = (k-0,3)/(p+0,4).

Метод подстановки

Если число опытов равно числу неизвестных параметров модели, то отклонения наблюдаемых в эксперименте значений у от расчетных ў во всех опытных точках равны нулю. Для определения значений неизвестных параметров модели решают систему линейных уравнений.

Систему линейных уравнений решают методом последовательного исключения неизвестных - методом Гаусса.

Пусть, например, имеется система трех уравнений с тремя неизвестными:

a₁₁ х₁+ а₁₂ х₂+ а₁₃ х₃ = b₁ ;

a₂₁ х₁+ а₂₂ х₂+ а₂₃ х₃ = b₂ ;

a₃₁ х₁+ а₃₂ х₂+ а₃₃ х₃ = b₃ .

Сначала исключают неизвестную х₁ во всех уравнениях, начиная со второго. Для этого коэффициенты и свободный член первого уравнения делят на первый коэффициент, полагая, что он не равен нулю (a₁₁¹0)

х₁ + (a₁₂ / a₁₁) x₂ + (a₁₃ / a₁₁) x₃ = b₁ / a₁₁ .

Значение неизвестной х₁ , равное

x₁ = - (a₁₂ / a₁₁) x₂ - (a₁₃ / a₁₁) x₃ + b₁ / a₁₁

или

x₁ = a₁₂ x₂ + a₁₃ x₃ + b₁ ,

подставляют во все уравнения, начиная со второго, и получают новую систему из двух уравнений с двумя неизвестными:

(a₂₂ + a₁₂a₂₁ ) x₂ + (a₂₃ + a₁₃a₂₁ ) x₃ = (b₂ +b₁ a₂₁) ;

(a₃₂ + a₁₂a₃₁ ) x₂ + (a₃₃ + a₁₃a₃₁ ) x₃ = (b₃ +b₁ a₃₁)

или

a¢₂₂ x₂ + a¢₂₃ x₃ = b'₂ ;

a¢₃₂ x₂ + a¢₃₃ x₃ = b'₃ .

Аналогичным способом исключают неизвестную х₂. Для этого коэффициенты и свободный член преобразованного второго уравнения делят на коэффициент перед неизвестной х₂, полагая, что он не равен нулю
(а'₂₂ ¹ 0).

х₂ + (а'₂₃ / а'₂₂) х₃ = b'₂ / a'₂₂ .

Значение неизвестной х₂ , равное

х₂ = - (a'₂₃ / a'₂₂ ) x₃ + b'₂ / a'₂₂

или

x₂ =α₂₃ x₃ +β₂ ,

подставляют в оставшееся третье уравнение

(a′₃₃+ a₂₃a′₃₂) x₃ = (b′₃ + b₂a′₃₂)

или

a″₃₃x₃ = b″₃₃ .

Отсюда находим значение неизвестной х₃

x₃ = b″₃ / a″₃₃=β₃ .

Затем формируют треугольную систему трех уравнений:

x₁ =α₂₂ x₂ + α₁₃ x₃ + β₁ ;

x₂ = α₂₃ x₃ + β₂ ;

x₃ = β₃ .

Значения неизвестных определяют в обратной последовательности, начиная с последнего

x₃ = b₃

x₂ = a₂₃ b₃ + b₂

x₁ = a₁₂ (a₂₂ b₂ + b₂) + a₁₃ b₃ + b₁ .

ОПТИМАЛЬНОЕ ПЛАНИРОВАНИЕ

Оптимальное планирование - процедура получения информации об оптимальном управляющем воздействии из информации об управляемом физическом процессе, информации о задаче управления и информации о методе решения задачи управления.

Информация об оптимальном управляющем воздействии представляется в виде оптимального плана. Оптимальный план представляет собой совокупность значений управляющих факторов, обеспечивающих достижение цели управления в заданных условиях с наибольшей эффективностью.