Методы построения математических моделей

Теоретические модели получают в результате логического анализа и формализации общих закономерностей исследуемого процесса. В основу метода построения теоретических моделей входят логическое обобщение имеющихся фактов и логический вывод результатов из небольшого числа основных принципов, законов и гипотез.

Использование аппарата математики и логики дает возможность понять внутреннюю структуру объекта исследования и повысить уровень достоверности знания о природе объекта.

Взаимосвязь и взаимозависимость различных величин, характеризующих разные по своей природе процессы, выражаются с помощью математических функций, полученных в результате математических преобразований.

Процесс подбора эмпирической формулы для устанавливаемой в эксперименте зависимости R = f(z) состоит из двух процедур: подбора вида формулы и установления численных значений ее параметров, для которых приближение к этой формуле оказывается наилучшим.

Если нет каких-либо соображений для подбора вида формулы, то выбирают функциональную зависимость из числа наиболее простых, сравнивая их графики с графиком идентифицируемой функции.

При рассмотрении графиков следует иметь в виду, что при пользовании эмпирическими формулами используется лишь часть кривой, соответствующая некоторому интервалу изменения аргумента.

К числу наиболее употребительных функций, применяемых при моделировании, относятся линейные, квадратные, кубические, степенные, экспоненциальные и экспоненциально-степенные.

Могут быть рекомендованы:

а) линейные полиномиальные модели

;

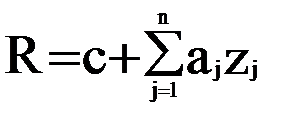б) квадратные полиномиальные модели

;

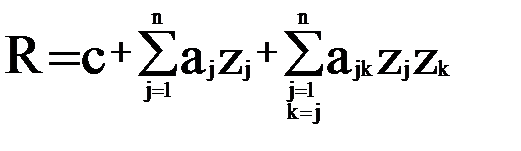в) кубические полиномиальные модели

;

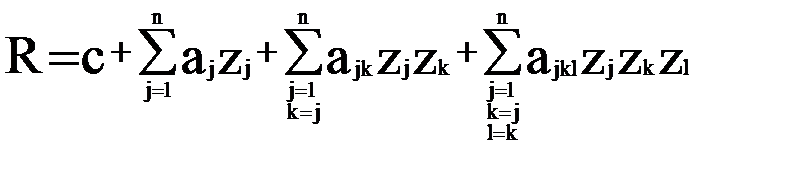г) экспоненциальные мультипликативные модели

.

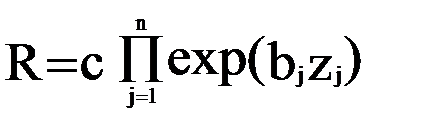Экспоненциальные мультипликативные модели логарифмированием приводят к линейным полиномиальным моделям

;

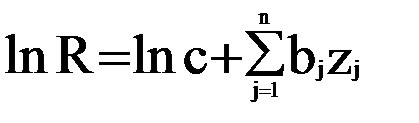д) степенные мультипликативные модели

.

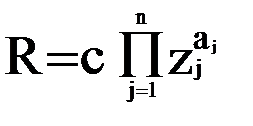е) экспоненциально-степенные мультипликативные модели

.

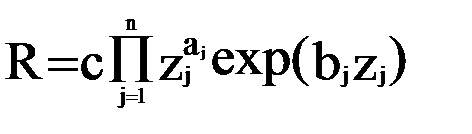Экспоненциально-степенные мультипликативные модели логарифмированием приводят к линейным полиномиальным моделям

.

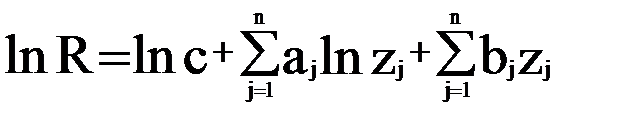Для описания случайных величин используют различные функции распределения. Среди этих распределений: экспоненциальное, степенное, Гнеденко и другие.

Функция распределения F(x) - вероятность появления значения случайной величины, не превышающего некоторого заданного х.

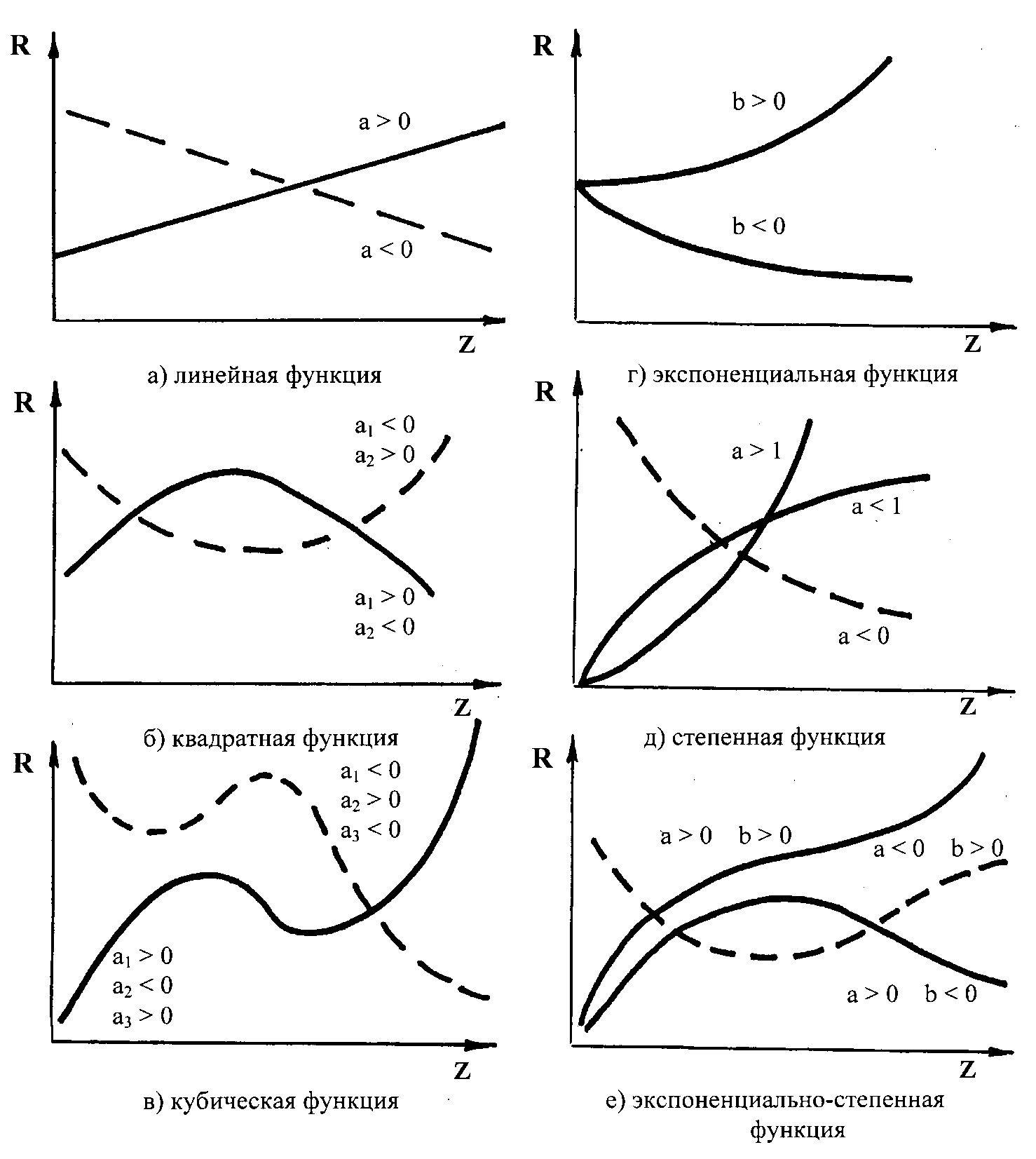
Рис. 5. Графики наиболее употребительных функций