Геометрическая вероятность.
Рассмотрим на плоскости некоторую область W, имеющую площадь SWи внутри области W область D c площадью SD. В области W случайно выбирается точка X. Этот выбор можно интерпретировать как бросание точки X в область W. При этом попадание точки в область W - достоверное событие, в D – случайное. Предполагается, что все точки области W равноправны (все элементарные события равновозможны), т.е. что брошенная точка может попасть в любую точку области W и вероятность попасть в область D пропорциональна площади этой области и не зависит от ее расположения и формы. Пусть событие 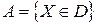 = {брошенная точка попадет в область D}.
= {брошенная точка попадет в область D}.
Определение. Геометрической вероятностью события А называется отношение площади области D к площади области W, т.е. 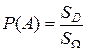 .
.
Замечание 1. Геометрическое определение вероятности события применимо и в случае, когда области D и W обе линейные 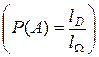 или объемные
или объемные 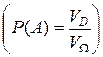 . Здесь
. Здесь 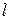 - длина,
- длина, 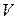 - объем.
- объем.
Замечание 2. Все три формулы можно записать в виде:  , где
, где  - мера (длина, площадь, объем) соответствующей области.
- мера (длина, площадь, объем) соответствующей области.
Пример1. В круг радиусом R=1 равномерно бросается точка. Найдем вероятность события А, что эта точка попадет в круг радиуса r=1/2 с тем же центром.
Решение. 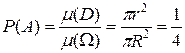
Пример 2. (Задача о встрече.) Два человека договорились о встрече между 9 и 10 часами утра. Пришедший первым ждет второго в течение 15 мин, после чего уходит (ели они не встретились). Найти вероятность того, что встреча состоится, если каждый наудачу выбирает момент своего прихода.
 Решение. Пусть х – время прихода первого, а у - второго. Возможные значения х и у:
Решение. Пусть х – время прихода первого, а у - второго. Возможные значения х и у: 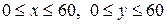 , которые на плоскости Оху определяют квадрат со стороной равной 60. Точки этого квадрата изображают время встречающихся. Тогда этот квадрат можно рассматривать как пространство
, которые на плоскости Оху определяют квадрат со стороной равной 60. Точки этого квадрата изображают время встречающихся. Тогда этот квадрат можно рассматривать как пространство 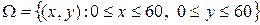 . Все исходы W равновозможны, так как лица приходят наудачу. Событие А = {лица встретятся} произойдет, если разность между моментами их прихода по модулю будет не более 15 мин, т.е.
. Все исходы W равновозможны, так как лица приходят наудачу. Событие А = {лица встретятся} произойдет, если разность между моментами их прихода по модулю будет не более 15 мин, т.е.  . Неравенство
. Неравенство 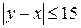 , т.е.
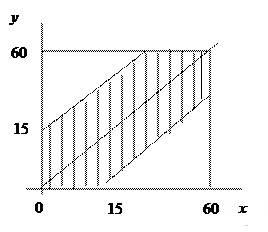
, т.е. 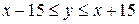 определяет область, заштрихованную на рисунке. Т.о., точки заштрихованной полосы есть исходы, благоприятствующие встрече. Тогда
определяет область, заштрихованную на рисунке. Т.о., точки заштрихованной полосы есть исходы, благоприятствующие встрече. Тогда 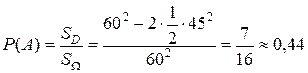 .
.
Пример 1. Из колоды, содержащей 36 карт, наудачу вынимают 3 карты. Найти вероятность того, что среди них окажется хотя бы одна дама.
Решение. Пусть А = {среди 3 карт окажется хотя бы одна дама}.
1) А1 = {среди 3 карт окажется ровно одна дама};
А2 = {среди 3 карт окажется ровно две дамы};
А3 = {среди 3 карт окажется ровно три дамы};
События 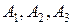 - несовместные. Очевидно, что
- несовместные. Очевидно, что  . Поэтому по аксиоме сложения
. Поэтому по аксиоме сложения 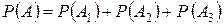 . Общее число исходов для всех трех событий равно
. Общее число исходов для всех трех событий равно 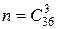 . Число исходов, благоприятных для событий
. Число исходов, благоприятных для событий 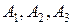 , соответственно равно
, соответственно равно  . Тогда
. Тогда
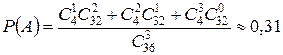 .
.
2) 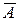 = {среди 3 карт нет ни одной дамы};
= {среди 3 карт нет ни одной дамы}; 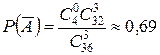 . Значит
. Значит 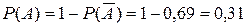 .
.
Дата добавления: 2016-03-04; просмотров: 1140;
