Геометрическая интерпретация игры размера 2×2
Решение игры размера 2×2 допускает наглядную геометрическую интерпретацию. Пусть игра не имеет седловой точки и задана платежной матрицей:
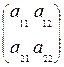
Если второй игрок применяет свою первую стратегию, то выигрыш первого игрока определяется формулой:
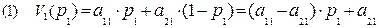 ;
;
Аналогично, если второй игрок применяет свою вторую чистую стратегию, то выигрыш первого игрока определяется формулой:
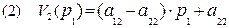 ;
;
Из формул (1) и (2) видно, что выигрыши первого игрока при чистых стратегиях второго игрока являются линейными функциями с аргументом 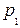 .
.
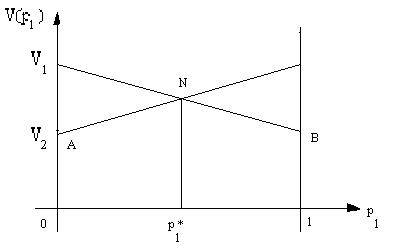
Построим графики функций  и
и 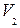 на отрезке [0, 1] изменения частоты
на отрезке [0, 1] изменения частоты 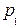 :
:
Рис. 1
В соответствии с принципом минимакса для смешанных стратегий, первый игрок должен выбрать частоту 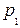 так, чтобы максимизировать свой выигрыш. Ординаты точек ломаной ANB показывают минимальный его выигрыш при использовании им любой смешанной стратегии. Ломаная ANB является нижней границей выигрышей первого игрока. Оптимальную стратегию
так, чтобы максимизировать свой выигрыш. Ординаты точек ломаной ANB показывают минимальный его выигрыш при использовании им любой смешанной стратегии. Ломаная ANB является нижней границей выигрышей первого игрока. Оптимальную стратегию 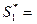
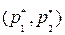 определяет точка N, в которой минимальный выигрыш достигает максимума. Это самая верхняя точка нижней границы выигрышей первого игрока. Ее ордината равна цене игры V.
определяет точка N, в которой минимальный выигрыш достигает максимума. Это самая верхняя точка нижней границы выигрышей первого игрока. Ее ордината равна цене игры V.
Заметим, что в игре размера 2×2 без седловой точки прямые  и
и 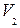 имеют противоположные наклоны, т.е. одна прямая составляет острый угол с осью
имеют противоположные наклоны, т.е. одна прямая составляет острый угол с осью 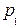 , другая – тупой, в противном случае игра будет иметь седловую точку, и решение будет в чистых стратегиях.
, другая – тупой, в противном случае игра будет иметь седловую точку, и решение будет в чистых стратегиях.
Применим геометрический метод для решения игры Эдварда и Фионы, заданной платежной матрицей 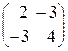 . Чтобы найти цену игры и оптимальную стратегию Эдварда, достаточно найти координаты точки N, для чего составим систему уравнений из формул (1) и (2):
. Чтобы найти цену игры и оптимальную стратегию Эдварда, достаточно найти координаты точки N, для чего составим систему уравнений из формул (1) и (2): 

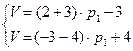
Решив систему, найдем, что 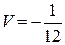 ,
, 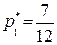 ,
, 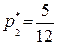 .
.
Дата добавления: 2016-04-14; просмотров: 961;
