Решение игры размера m×n с помощью линейного программирования
В общем случае игра размера m×n не имеет геометрической интерпретации, и для нее нет аналитического решения. Однако теория игр тесно связана с линейным программированием. Любая конечная игра с нулевой суммой может быть представлена в виде задачи линейного программирования и, наоборот, любая задача линейного программирования может быть представлена как конечная игра. Первым установил эту связь американский математик Д. Нейман. Покажем, свести решение игры размера m×n к решению задачи линейного программирования.
Пусть игра задана платежной матрицей A:
A = 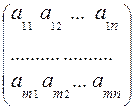 , i = 1, 2,…, m; j = 1, 2, …, n.
, i = 1, 2,…, m; j = 1, 2, …, n.
Можно считать, что цена игры V > 0; этого можно добиться, увеличив все элементы матрицы A на достаточно большое положительное число k. При этом преобразовании матрицы A цена игры также увеличится на k. Оптимальная стратегия первого игрока 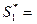
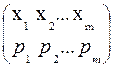 ,
, 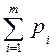 =1, обеспечивает ему средний выигрыш, не меньший, чем цена игры V, при любой чистой j = 1, 2, …, n стратегии второго игрока, поэтому получаем систему n линейных неравенств:
=1, обеспечивает ему средний выигрыш, не меньший, чем цена игры V, при любой чистой j = 1, 2, …, n стратегии второго игрока, поэтому получаем систему n линейных неравенств:
(1) 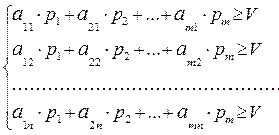
Разделим каждое из неравенств на число V > 0 и введем новые переменные 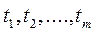 , определяемые по формуле:
, определяемые по формуле:
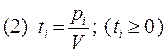
Так как 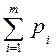 =1, то
=1, то 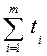 =
= 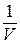 . Система (1) примет вид:
. Система (1) примет вид:
 (3)
(3) 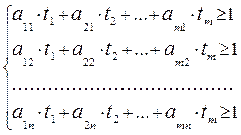
Цель первого игрока – максимизировать свой выигрыш, т.е. цену игры V. Это эквивалентно тому, что ему требуется минимизировать величину 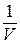 =
= 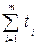 . Тогда задачу первого игрока можно сформулировать так: найти неотрицательные значения переменных
. Тогда задачу первого игрока можно сформулировать так: найти неотрицательные значения переменных 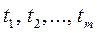 , удовлетворяющие системе линейных неравенств (3), при которых линейная функция z =
, удовлетворяющие системе линейных неравенств (3), при которых линейная функция z = 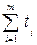 принимает минимальное значение. Мы получили задачу линейного программирования. Решив ее симплекс– методом, перейдем, используя формулы (2), к старым переменным
принимает минимальное значение. Мы получили задачу линейного программирования. Решив ее симплекс– методом, перейдем, используя формулы (2), к старым переменным 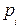 и получим оптимальную стратегию
и получим оптимальную стратегию 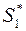 первого игрока и цену игры V.
первого игрока и цену игры V.
Для определения оптимальной стратегии второго игрока:
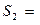
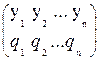 ,
, 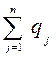 =1,
=1,
следует учесть, что она обеспечивает ему средний проигрыш не больший, чем цена игры V, при любой чистой i = 1, 2, …, m стратегии первого игрока, поэтому получаем систему m линейных неравенств:
(4) 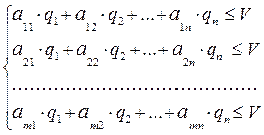
Разделим каждое из неравенств на число V > 0 и введем новые переменные 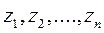 , определяемые по формуле:
, определяемые по формуле:
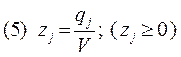
Так как 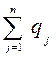 =1, то
=1, то 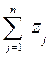 =
= 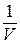 . Система (4) примет вид:
. Система (4) примет вид:
(6) 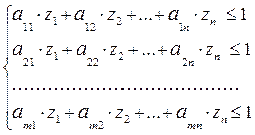
Цель второго игрока – минимизировать свой проигрыш, т.е. цену игры V. Это эквивалентно тому, что ему требуется максимизировать величину 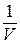 =
= 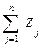 . Тогда задачу второго игрока можно сформулировать так: найти неотрицательные значения переменных
. Тогда задачу второго игрока можно сформулировать так: найти неотрицательные значения переменных 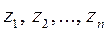 , удовлетворяющие системе линейных неравенств (6), при которых линейная функция f =
, удовлетворяющие системе линейных неравенств (6), при которых линейная функция f = 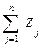 принимает минимальное значение. Мы снова получили задачу линейного программирования. Решив ее симплекс– методом, перейдем, используя формулы (5), к старым переменным
принимает минимальное значение. Мы снова получили задачу линейного программирования. Решив ее симплекс– методом, перейдем, используя формулы (5), к старым переменным 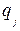 и получим оптимальную стратегию
и получим оптимальную стратегию 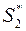 второго игрока.
второго игрока.
Отметим, что задача для второго игрока с системой ограничений (6) является двойственной к задаче первого игрока с системой ограничений (3).
Пример 4. Найти решение игры с платежной матрицей
 A =
A = 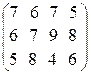
Для решения игры применим систему компьютерной алгебры Maple. Подключим модуль simplex, зададим систему неравенств (3) под именем sn, определим функцию z = t1+t2+t3 и найдем оптимальное решение задачи линейного программирования с помощью стандартной функции mininmize:
> with(simplex);
>sn:={7*t1+6*t2+5*t3>=1, 6*t1+7*t2+8*t3>=1, 7*t1+9*t2+4*t3>=1,
5*t1+8*t2+6*t3>=1};
> z:=t1+t2+t3;
> minimize(z, sn, NONNEGATIVE); {t3 = 0, t2 = 1/13, t1 = 1/13}
Так как t1+ t2 + t3 = 2/13 = 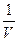 , то цена игры V = 6,5 и, используя формулу (2), находим :
, то цена игры V = 6,5 и, используя формулу (2), находим : 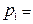 t1*V = 0,5,
t1*V = 0,5, 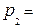 t2*V = 0,5,
t2*V = 0,5, 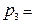 0.
0.
Для вычисления оптимальной стратегии второго игрока, снова применим Maple, задавая систему (6) под именем cn и максимизируя функцию f = z1+z2+z3+z4:
> with(simplex);
>cn:={7*z1+6*z2+7*z3+5*z4<=1, 6*z1+7*z2+9*z3+8*z4<=1,
5*z1+8*z2+4*z3+6*z4<=1};
> f:=z1+z2+z3+z4;
> maximize(f, cn, NONNEGAT IVE}; {z2 =1/13, z1 =1/13, z4 = 0, z3 = 0}
Так как цена игры V = 6,5, то, используя формулу (5), находим:
 z1*V = 0,5,
z1*V = 0,5, 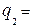 t2*V = 0,5,
t2*V = 0,5, 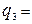 0,
0, 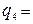 0.
0.
Ниже приводится программа вычисления решения игры симплекс–методом. Предполагается, что размеры платежной матрицы не превышают 20. Информация о платежной матрице хранится в текстовом файле ‘input.txt’. В его первой строке записаны 2 целых числа – размеры m и n. Далее в m строках располагаются элементы платежной матрицы A по n чисел в каждой строке. Для определенной выше игры файл ‘input.txt’ имеет вид:
3 4
7 6 7 5
6 7 9 8
5 8 4 6
Процедура readf считывает данные из файла и выводит эти данные на экран. Процедура sedlo проверяет, имеет ли платежная матрица седловую точку и выводит чистые оптимальные стратегии игроков, если игра с седловой точкой. В противном случае с помощью процедуры change все элементы платежной матрицы увеличиваются на одну и ту же величину, так, чтобы они стали все положительными; далее матрица расширяется и преобразуется в матрицу коэффициентов соответствующей задачи линейного программирования.
Процедура simplex находит решение задачи линейного программирования. В основной части программы из этого решения по рассмотренным выше формулам вычисляются оптимальные смешанные стратегии игроков и цена игры:
program game;
{$N+} {$R-}
uses crt;
type te=extended;
const nn=20;mm=20;
var a:array[1..mm,1..nn] of te; t,i,j,m,n:integer;
p:array[1..mm] of te; q:array[1..nn] of te;
z,min,v:te; h:boolean; f:text;
procedure readf;
begin assign(f,'input.txt');
reset(f); readln(f,m,n);
for i:=1 to m do
for j:=1 to n do read(f,a[i,j]);
close(f);
writeln('РАЗМЕРЫ ИГРЫ: m=',m,' n=',n) ;
writeln(' ПЛАТЕЖНАЯ МАТРИЦА ИГРЫ: ') ;
for i:=1 to m do
begin
for j:=1 to n do write(a[i,j]:4:1); writeln
end
end;
procedure sedlo;
var i,j,k,l,q:integer; t,b:boolean;
p:array[1..nn] of integer; min:te;
begin i:=1; t:=false;
while (i<=m) and (not t) do
begin min:=a[i,1]; q:=1;
for j:=2 to n do
if min>a[i,j] then begin min:=a[i,j]; q:=j
end;
k:=0;
for j:=1 to n do if a[i,j]=min then
begin k:=k+1; p[k]:=j
end;
for l:=1 to k do
begin b:=true;
for j:=1 to m do
if a[i,p[l]]<a[j,p[l]] then
begin b:=false; j:=m
end;
if b then
begin writeln('есть седловая точка');
writeln('цена игры=',a[i,q]:4:2);
writeln('опт. стратегия 1 игрока: ',i);
writeln('опт. стратегия 2 игрока: ',p[l]);
readln; readln;
t:=true; l:=k;
end;
end;
i:=i+1;
end; h:=t;
if (not t) then
begin writeln('седловой точки нет');
writeln('ищем смешанные оптимальные стратегии');
end
end;
procedure change;
begin
for i:=1 to m do p[i]:=0;
for j:=1 to n do q[j]:=0;
min:=0;
for i:=1 to m do
for j:=1 to n do
if A[i,j]<min then min:=a[i,j]; writeln;
min:=min-1;
for i:=1 to m do
for j:=1 to n do
a[i,j]:=a[i,j]-min;
t:=m+n+1;
for i:=1 to (m+1) do
for j:=(n+1) to m+n do a[i,j]:=0;
for j:=1 to n do a[m+1,j]:=-1;
for i:=1 to m do
begin a[i,n+i]:=1; a[i,t]:=1;a[i,t+1]:=0
end;
a[m+1,t]:=0;
end;
procedure simplex;
var s,r:integer; c,w:te; b:boolean;
begin writeln;
s:=1;
for j:=2 to n+m do
if a[m+1,j]<a[m+1,s] then s:=j;
if a[m+1,s]<0 then
begin
b:=true;
repeat r:=0;
repeat
r:=r+1
until a[r,s]>=1.0e-20;
for i:=r+1 to m do
begin c:=a[r,n+m+1]/a[r,s];
if a[i,s]>=1.0e-20 then
if a[i,t]/a[i,s]<c then r:=i
end;
a[r,t+1]:=s;
if s>n then a[r,t+1]:=0;
w:=a[r,s];
for j:=1 to t do
a[r,j]:=a[r,j]/w;
for i:=1 to m+1 do
begin if i<>r then
begin
w:=a[i,s];
if abs(w)>=1.0e-20 then
for j:=1 to t do a[i,j]:=a[i,j]-a[r,j]*w
end;
end; s:=1;
for j:=2 to n+m do
if a[m+1,j]<a[m+1,s] then s:=j;
if a[m+1,s]<0 then b:=false else b:=true
until b;
end;
end;
begin clrscr;
readf;
writeln;
sedlo;
if not h then
begin
change;
simplex;
v:=1/a[m+1,n+m+1];
for i:=1 to m do
p[i]:=a[m+1,n+i]*v;
for j:=1 to n do
q[round(a[j,t+1])]:=a[j,t]*v;
writeln;
writeln('оптимальные стратегии первого игрока:');
for i:=1 to m do
write(p[i]:4:3,' ' ); writeln;
writeln('оптимальные стратегии второго игрока:');
for j:=1 to n do
write(q[j]:4:3,' '); writeln;
writeln('цена игры (для первого игрока): ',(v+min):4:3);
end ; readkey
end.
В некоторых случаях игру размера m×n можно упростить, удаляя «доминируемые» стратегии игроков. Стратегия с номером i первого игрока доминируется k – той его стратегией, если все элементы строки i платежной матрицы не больше соответствующих элементов строки k, т.е. 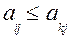 для j = 1,2, …, n. Поэтому доминируемая i – тая стратегия первого игрока хуже его k – тoй стратегии и ее можно не использовать в игре. Аналогично определяется доминируемая стратегия второго игрока, приносящая ему больший проигрыш, чем другая его стратегия.
для j = 1,2, …, n. Поэтому доминируемая i – тая стратегия первого игрока хуже его k – тoй стратегии и ее можно не использовать в игре. Аналогично определяется доминируемая стратегия второго игрока, приносящая ему больший проигрыш, чем другая его стратегия.
Пример 5. Найти решение игры с платежной матрицей
 A =
A = 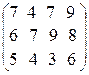
Решение. Третья стратегия первого игрока доминируется второй, поэтому ее можно отбросить. После этого третья и четвертая стратегии второго игрока доминируются его второй стратегией, и их также можно удалить. Получаем игру размера 2×2 с платежной матрицей 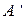 =
= 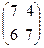 . Эта игра без седловой точки
. Эта игра без седловой точки 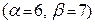 и легко решается аналитически:
и легко решается аналитически: 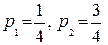 , цена игры V=6,25,
, цена игры V=6,25, 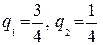 .
.
Дата добавления: 2016-04-14; просмотров: 1250;
