Геометрическая интерпретация устойчивости

Дадим геометрическую интерпретацию устойчивости по начальным данным. Для простоты рассмотрим однородное уравнение (3), т.е. при f(t,x) = 0. Общее решение однородного уравнения переноса имеет вид (4): 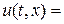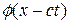, т.е. значения решения переносятся вдоль характеристики x - ct = const без изменения.

Рассмотрим разностную схему (7а) с шаблоном на рис.6,а (аналогичный шаблон приведен на рис.2,а). На рис.6,а стрелкой обозначена характеристика, приходящая в точку (t_m ₊₁,x_n). Характеристика пересекает слой t_m в точке 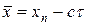. Точка пересечения находится согласно определению характеристики: 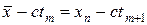= const.


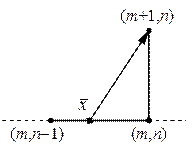
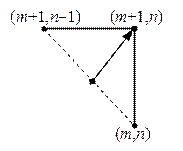
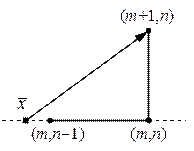
Рис.6,а. Перенос значения функции по характеристике при выполнении условия Куранта (для схемы (7а))	Рис.6,б. Перенос значения функции по характеристике при нарушении условия Куранта (для схемы (7а))	Рис.6,в. Перенос значения функции по характеристике при любых значениях t и h (для схемы (7в))

Найдем решение в точке 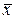с помощью линейной интерполяции разностного решения между двумя узлами шаблона рис.6,а на слое t_m, тогда

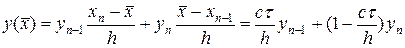Далее полученное значение из точки 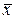переносим без изменения по характеристике в узел (t_m ₊₁,x_n), т.е. положим .

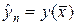Выполнение условия устойчивости для схемы (7а) ct £ h обеспечивает попадание точки 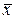в полуинтервал [x_n _-₁,x_n), т.е. 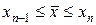. Если условие устойчивости нарушается, точка 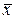становится меньше x_n _-₁, т.е. 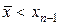при ct > h. В этой ситуации решение в точке 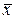находится с помощью экстраполяции. Другими словами, схема (7а) устойчива, если 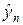вычисляется по значениям с предыдущего слоя при помощи интерполяции (рис.6,а). Схема (7а) неустойчива, если при вычислении величины 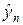используется экстраполяция (рис.6,б).

Разностные схемы (7б), (7в) можно также интерпретировать как линейные интерполяции по двум уже вычисленным значениям с переносом полученного значения по характеристике. Так, безусловная устойчивость схемы (7в) обязана тому, что приходящая в узел (t_m ₊₁,x_n) характеристика при любых t и h пересекает отрезок (пунктирная линия на рис.6,в), соединяющий узлы интерполяции значения решения, которое по характеристике переносится в узел (t_m ₊₁,x_n).

Разностная схема (7г) также может быть истолкована как интерполяция, но не двухточечная, а трехточечная. Учитывая рис.2,г видно, что при любом выборе шагов t и h приходящая в узел (t_m ₊₁,x_n) характеристика переносит значение, которое вычисляется с помощью интерполяции по ранее вычисленным значениям.

Данная геометрическая интерпретация полезна тем, что по имеющейся характеристике можно подобрать шаблон разностной схемы так, чтобы было выполнено требование устойчивости. Рассмотрим некоторые примеры.

Явно-неявная схема. Будем считать, что шаг по времени 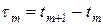и по пространству 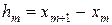не постоянны, а скорость переноса переменная величина, т.е. c = c(t,x). При вычислении 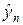проверим условие Куранта (8) в текущей ячейке. Если условие Куранта выполняется, то используем схему (7а):

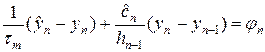, (15)

если условие Куранта в форме (8) нарушается, используем схему (7б):

. (15¢)

Явно-неявная схема (15), (15¢) безусловно устойчива, причем невязка этой схемы меньше, чем у безусловно устойчивой схемы (7в). Схему (15), (15¢) используют в том случае, когда искомое решение является недостаточно гладким или быстропеременным.

Сравним разностные схемы (15), (15¢) и (7в) на примере решения задачи:

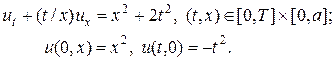(16)

Решение задачи (16) можно легко найти

. (17)

На листинге_№4 приведен код программы численного решения задачи (16) и сравнения полученного решения с аналитическим решением (17). Сравнение производится в норме 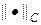, т.е. error = .

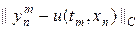Листинг_№4

%Программа сравнения явно-неявной схемы для решения

%уравнения переноса с безусловно устойчивой схемой (7в)

function obvious

%Определяем пределы интегрирования уравнения переноса

%по времени и по пространству, [0,T]x[0,a]

T=1; a=1; kmax=300; l=1;

for k=50:50:kmax

%Определяем число узлов сетки по времени и

%по пространству

Nt=k; Nx=k;

%Определяем неравномерную сетку по времени

t(1)=0;

for m=1:(Nt-1)

t(m+1)=t(m)+(T/(Nt-1))*(1+0.1*randn);

end

%Определяем неравномерную сетку по пространству

x(1)=0;

for n=1:(Nx-1)

x(n+1)=x(n)+(a/(Nx-1))*(1+0.1*randn);

end

%Задаем левое граничное условие u(t,0)=-t^2

for m=1:Nt

y(m,1)=-t(m)^2;

end

%Задаем начальные данные u(0,x)=x^2

for n=1:Nx

y(1,n)=x(n)^2;

end

%Организуем цикл расчетов по явно-неявной

%схеме (15), (15')

for m=1:(Nt-1)

tau=t(m+1)-t(m);

for n=2:Nx

h=x(n)-x(n-1); c=t(m+1)/x(n); r=(tau*c)/h;

if r<=1

y(m+1,n)=(1-r)*y(m,n)+r*y(m,n-1)+...

tau*f(t(m)+0.5*tau,x(n)-0.5*h);

else

y(m+1,n)=(1-1/r)*y(m+1,n-1)+y(m,n-1)/r+...

(tau/r)*f(t(m)+0.5*tau,x(n)-0.5*h);

end

%Находим различие между численным и

%аналитическим решениями

for m=1:Nt

for n=1:Nx

yerror(m,n)=abs(y(m,n)-ya(t(m),x(n)));

end

%Выводим ошибку численного решения в норме C

error_obvious(l)=max(max(yerror));

%Организуем расчет по безусловно устойчивой схеме (7в)

for m=1:(Nt-1)

tau=t(m+1)-t(m);

for n=2:Nx

h=x(n)-x(n-1); c=t(m+1)/x(n); r=(tau*c)/h;

y(m+1,n)=(r/(1+r))*y(m+1,n-1)+y(m,n)/(1+r)+...

(tau/(1+r))*f(t(m)+0.5*tau,x(n)-0.5*h);

end

%Находим различие между численным и

%аналитическим решениями

for m=1:Nt

for n=1:Nx

yerror(m,n)=abs(y(m,n)-ya(t(m),x(n)));

end

%Выводим ошибку численного решения в норме C

error_non_obvious(l)=max(max(yerror));

l=l+1;

end

plot(50:50:kmax,error_obvious,'-*', ...

50:50:kmax,error_non_obvious,'-p','MarkerSize',12);

%Определяем функцию, возвращающую правую часть уравнения

function y=f(t,x)

y=x^2+2*t^2;

%Определяем аналитическое решение уравнения переноса

function y=ya(t,x)

y=x^2-t^2+x^2*t;

На рис.7 приведен итоговый график сравнения явно-неявной схемы (15), (15¢) и безусловно устойчивой неявной схемы (7в) на примере решения задачи (16), (17). На графике по оси абсцисс отложено число точек сетки по времени и по пространству, по оси ординат — ошибка как разность численного и аналитического решений в норме 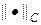. Из графика отчетливо видно, что явно-неявная схема более точна, чем безусловно устойчивая неявная схема.

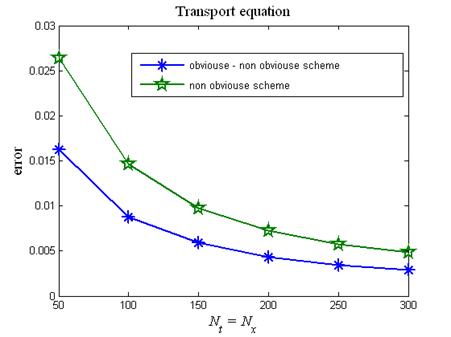
Рис.7. Сравнение ошибок при расчетах по явно-неявной (15), (15¢) и
безусловно устойчивой неявной (7в) разностных схем

Схема без шаблона. Рассмотрим характеристику, которая приходит в узел (t_m₊₁,x_n) и которая пересекает слой t_m в точке 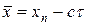. Найдем пару узлов 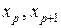на слое t_m, между которыми попадает точка 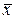. Определим 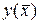с помощью линейной интерполяции по значениям :

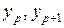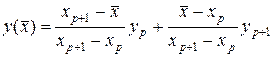, (18)

при этом 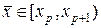. Переносим значение 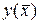по характеристике в узел (t_m₊₁,x_n), т.е. полагаем 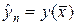. В соответствии с геометрическим смыслом устойчивости, разностная схема (18) безусловно устойчива.

В разностной схеме (18) положение пары узлов 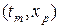и относительно узла (t_m₊₁,x_n) не определено, когда скорость c = c(t,x) не фиксирована или сетка по пространству не равномерна. Это означает, что разностная схема (18) является схемой без шаблона.

Изучим поведение точности схемы (18) на примере решения задачи:

(19)

Решение задачи (19) можно легко найти

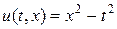. (20)

На листинге_№5 приведен код программы, которая с помощью схемы без шаблона численно решает задачу (19). На выходе работы программы строится график ошибки численного решения error = 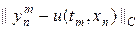в зависимости от числа узлов сетки по времени и по пространству (N_t = N_x). Данный график приведен на рис.8. График на рис.8 демонстрирует “правильное” поведение ошибки, она уменьшается по мере роста числа узлов одновременно по времени и по пространству.

Листинг_№5

%Программа тестирования схемы без шаблона для

%численного решения уравнения переноса (19)

function witht_template

%Определяем пределы интегрирования уравнения

%переноса по времени и по пространству, [0,T]x[0,a]

T=1; a=1; kmax=400; l=1;

for k=50:50:kmax

%Определяем число узлов сетки по времени и

%по пространству

Nt=k; Nx=k;

%Определяем неравномерную сетку по времени

t(1)=0;

for m=1:(Nt-1)

t(m+1)=t(m)+(T/(Nt-1))*(1+0.1*randn);

end

%Определяем неравномерную сетку по пространству

x(1)=0;

for n=1:(Nx-1)

x(n+1)=x(n)+(a/(Nx-1))*(1+0.1*randn);

end

%Задаем левое граничное условие u(t,0)=-t^2

for m=1:Nt

y(m,1)=-t(m)^2;

end

%Задаем начальные данные u(0,x)=x^2

for n=1:Nx

y(1,n)=x(n)^2;

end

%Организуем цикл расчетов по схеме без шаблона

for m=1:(Nt-1)

tau=t(m+1)-t(m);

for n=2:Nx

c=t(m+1)/x(n); xa=x(n)-c*tau;

p=1;

while (~((xa>=x(p))&(xa<x(p+1))))&((p+1)~=Nx)

p=p+1;

end

if xa>0

%интерполяция

y(m+1,n)=((x(p+1)-xa)/(x(p+1)-x(p)))*...

y(m,p)+((xa-x(p))/(x(p+1)-x(p)))*y(m,p+1);

else

y(m+1,n)=-(t(m)-xa/c)^2;

end

%Находим различие между численным и

%аналитическим решениями

for m=1:Nt

for n=1:Nx

yerror(m,n)=abs(y(m,n)-ya(t(m),x(n)));

end

%Запоминаем ошибку численного решения в норме C

error_without_template(l)=max(max(yerror));

l=l+1;

end

%Рисуем зависимость ошибки численного решения от

%количества узлов сетки по пространству и времени

plot(50:50:kmax,error_without_template,...

'-*','MarkerSize',12);

%Определяем аналитическое решение (20) уравнения переноса

function y=ya(t,x)

y=x^2-t^2;

Знакопеременная скорость переноса c(t,x). В этом случае задача поставлена корректно, когда условия поставлены на тех границах, характеристики из которых идут внутрь области G(t,x).

Пусть скорость c(t,x) непрерывна в области G(t,x) = [0,T]´[0,a] и меняет знак на линии 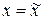, т.е. , при этом будем считать 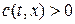, 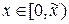и , .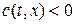

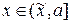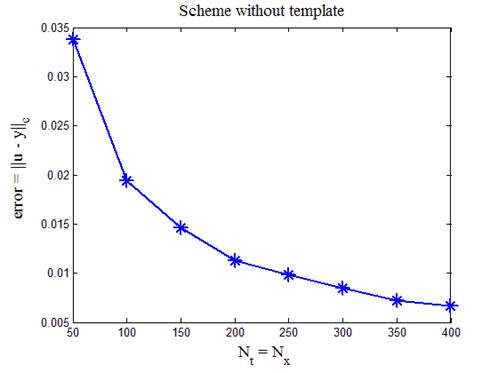
Рис.8. Зависимость ошибки численного решения задачи (19), (20)
от числа узлов сетки по времени и пространству
для схемы без шаблона

Для примера рассмотрим уравнение переноса следующего вида

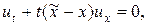(21)

где 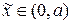. Найдем вид характеристик для уравнения (21). Для этого необходимо решить обыкновенное дифференциальное уравнение

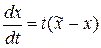. (22)

Решение уравнения (22) легко найти. Решение содержит две ветви, из которых выбираем положительную (t > 0), т.е.

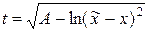, A = const. (23)

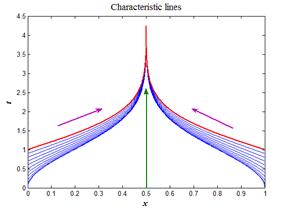
Нарисуем характеристики (23) средствами MATLAB. На листинге_№6 приведен короткий код программы рисования характеристик (23). Итог работы кода программы листинга_№6 приведен на рис.9,а. В целях упрощения кода на рис.9,а нарисованы лишь те характеристики, которые выпущены из левой и правой границ области G(t,x) = [0,T]´[0,a]. Стрелкой на рис.9,а обозначена линия, на которой скорость переноса обращается в ноль.

Листинг_№6

%Программа рисования характеристик

%t=sqrt(A-ln(xv-x)^2) уравнения

%du/dt+t(xv-x)du/dx=0

%очищаем рабочее пространство

clear all

%задаем размеры области G=[0,T]x[0,a]

T=1; a=1;

%определяем координату xv, на которой

%скорость переноса меняет знак

xv=0.5;

t=0:0.1:T;

%Определяем значения константы A

for m=1:length(t)

A(m)=t(m)^2+log(xv^2);

end

%Рисуем характеристики, выходящие из

%левой границы области G=[0,T]x[0,a]

x=0:0.001:(xv-1e-4);

for m=1:length(A)

for n=1:length(x)

y(n)=sqrt(A(m)-log((xv-x(n))^2));

end

plot(x,y);

hold on

end

%Рисуем характеристики, выходящие из

%правой границы области G=[0,T]x[0,a]

x=(xv-1e-4):0.001:a;

for m=1:length(A)

for n=1:length(x)

y(n)=sqrt(A(m)-log((xv-x(n))^2));

end

plot(x,y);

hold on

end


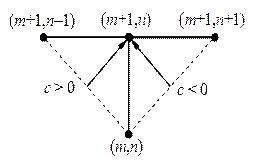
Рис.9,а. Характеристики (23) уравнения (21)	Рис.9,б. Шаблон разностной схемы для уравнения (24)

Возвращаясь к вопросу о корректности уравнения переноса со скоростью переноса меняющей знак и учитывая пример (21) — (23), можно констатировать, что необходимо задавать два граничных условия на левой и правой границах области G(t,x) = [0,T]´[0,a], т.е.

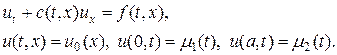(24)

Согласно (24), каждая из двух границ области (левая и правая) имеют свою зону влияния, которые разделены линией (вертикальная стрелка на рис.9,а). В каждой зоне можно использовать свою схему бегущего счета с учетом направления расчета.

Есть и другой способ. Построим для шаблона рис.9,б неявную разностную схему:

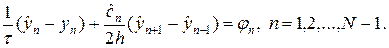(25)

С учетом направления характеристик (стрелки на рис.9,а) и принимая во внимание шаблон на рис.9,б видно, что при любом знаке скорости c и при любом соотношении шагов по времени t и пространству h значение 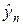вычисляется интерполяцией. Методом разделения переменных можно убедиться, что схема устойчива при любом знаке c.

Поскольку разностная схема на следующем слое связывает три соседних узла, постольку для решения полученной системы уравнений необходимо привлекать метод прогонки. Теоретические основы метода прогонки обсуждались в лекции №5. Применяя достаточное условие устойчивости метода прогонки (условие диагонального преобладания), приходим к условию Куранта в форме:

. (26)

Условие Куранта (26) для применимости метода прогонки является достаточным, поэтому при его нарушении схема (25) может все еще давать разумные численные решения. Исследуем этот вопрос на примере решения дачи (24) в виде:

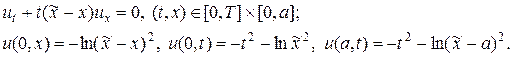(27)

Задача (27) имеет аналитическое решение

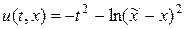На листинге_№7 приведен код программы численного решения задачи (27) с помощью разностной схемы (25) для сеток разной длины по времени и пространству.

Листинг_№7

%Программа численного решения задачи (27)

%Очищаем рабочее пространство

clear all

%Определяем область интегрирования G=[0,T]x[0,a] и

%прямую x=xv, на которой скорость в уравнении

%переноса меняет знак

T=1; a=1; xv=0.5;

k=1;

%Организуем цикл решения задачи (27) для различных

%сеток: Nt - число узлов в сетке по времени,

%Nx - число узлов в сетке по пространству

for Nt=10:10:100

for Nx=10:10:100

%вычисляем шаг по времени и по пространству

tau=T/(Nt-1); h=a/(Nx-1);

%определяем начальное условие

for n=1:Nx

y(1,n)=-log((xv-h*(n-1))^2);

end

%программируем процедуру прогонки решения

%задачи (27) по разностной схеме (25)

for m=1:(Nt-1)

alpha(2)=0;

beta(2)=-(tau*m)^2-log(xv^2);

for n=2:(Nx-1)

c=tau*m*(xv-h*(n-1));

r=(tau*c)/(2*h);

alpha(n+1)=-r/(1-r*alpha(n));

beta(n+1)=(y(m,n)+r*beta(n))/...

(1-r*alpha(n));

end

y(m+1,Nx)=-(tau*m)^2-log((xv-a)^2);

for n=Nx:-1:2

y(m+1,n-1)=alpha(n)*y(m+1,n)+beta(n);

end

%оцениваем ошибку численного решения, как

%разность численного решения и аналитического

%решения в норме l2

s=0;

for m=2:(Nt-1)

for n=2:(Nx-1)

s=(y(m,n)+(tau*(m-1))^2+...

log((xv-h*(n-1))^2))^2*tau*h;

end

%запоминаем норму ошибки и число узлов NtNx

%разностной схемы в области интегрирования G

error_l2(k)=sqrt(s);

gr(k)=Nt*Nx;

k=k+1;

end

t=0:tau:T;

x=0:h:a;

%Рисуем численное решение задачи (27) в области G

%с максимальным количеством узлов NtNx

subplot(1,2,1); surf(x,t,y);

%Рисуем график зависимости ошибки численного

%решения задачи (27) в норме l2 от произведения NtNx

subplot(1,2,2); plot(gr,error_l2);

На рис.10 приведен итог работы кода программы листинга_№7. На рис.10 слева изображено численное решение задачи (27) согласно разностной схеме (25) при выборе области интегрирования G(t,x) = [0,1]´[0,1]. По времени и пространству выбирались равномерные сетки: 0 = t₁ < … < t₁₀₀ = 1 и 0 = x₁ < … < x₁₀₀ = 1. На рис.10 справа приведен график зависимости разности численного и аналитического решений в норме 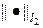от числа узлов сетки в области G(t,x) = [0,1]´[0,1]. Если число узлов по времени N_t, а по пространству — N_x, то общее число узлов сетки N_t´N_x. Из графика видна тенденция уменьшения ошибки в норме 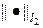по мере роста числа узлов сетки N_t´N_x.

Вернемся теперь к условию Куранта в форме (26). Для параметров задачи (27), выбранных в листинге_№7, соотношение Куранта варьировалось в довольно широком диапазоне 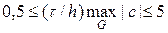( 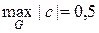), при этом проблем с устойчивостью численного решения методом прогонки не наблюдалось.

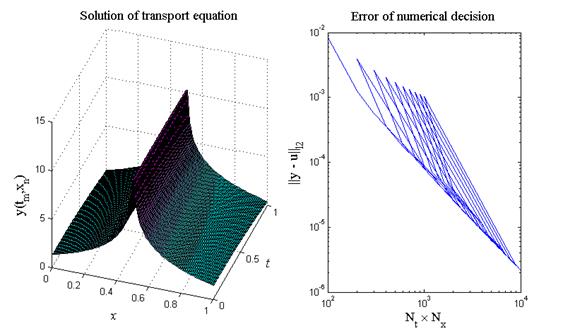
Рис.10.Численное решение задачи (27) (рисунок слева) и зависимость ошибки
численного решения в норме от числа узлов сетки в области
интегрирования G = [0,T]´[0,a] (рисунок справа)

123

Дата добавления: 2016-03-27; просмотров: 1317;